【模拟通信】AM、FM等的调制解调
樊昌信《通信原理》第五章 模拟调制系统 重点内容
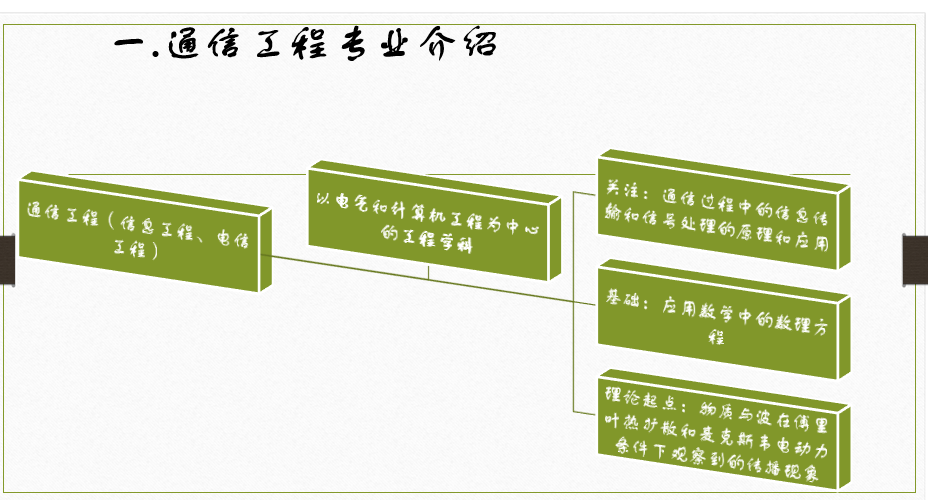
调制相关的概念
调制:控制载波的参数,使载波参数随调制信号的规律变化
已调信号:受调载波,含有调制信号的全部特征
调制的作用:
- 提高发射效率
- 多路复用,提高信道利用率
- 提高系统抗干扰能力
两种调制方式
线性调制(幅度调制)
线性调制的通用模型
-
一般模型

已调信号 s m ( t ) s_m(t) sm(t)的频谱 S m ( w ) S_m(w) Sm(w)只是按照载波的频率进行简单的搬移(线性),故幅度调制称为线性调制 -
抗噪声性能

-
抗噪声性能指标
输出信噪比 S 0 N 0 = m o 2 ( t ) ‾ n o 2 ( t ) ‾ \frac{S_0}{N_0}=\frac{\overline{m_o^2(t)}}{\overline{n_o^2(t)}} N0S0=no2(t)mo2(t)
调制制度增益(信噪比增益) G = S 0 / N 0 S i / N i G=\frac{S_0/N_0}{S_i/N_i} G=Si/NiS0/N0
输入噪声功率 N i = n 0 B N_i=n_0B Ni=n0B 注意 n 0 n_0 n0为单边功率谱密度(高斯白噪声双边谱密度乘以2)
AM–调幅
已调信号
s
A
M
(
t
)
=
[
A
0
+
m
(
t
)
]
c
o
s
w
c
t
s_{AM}(t)=[A_0+m(t)]cosw_ct
sAM(t)=[A0+m(t)]coswct
A
0
c
o
s
w
c
t
A_0cosw_ct
A0coswct:载波项
m ( t ) c o s w c t m(t)cosw_ct m(t)coswct:边带项
S A M ( w ) = π A 0 [ σ ( w + w c ) + σ ( w − w c ) ] + 1 2 [ M ( w + w c ) + M ( w − w c ) ] S_{AM}(w)=\pi A_0 [\sigma (w+w_c)+\sigma (w-w_c)]+\frac{1}{2}[M(w+w_c)+M(w-w_c)] SAM(w)=πA0[σ(w+wc)+σ(w−wc)]+21[M(w+wc)+M(w−wc)]
AM调制需要满足的条件:调制信号
m
(
t
)
m(t)
m(t)和叠加的直流偏量
A
0
A_0
A0需满足
∣
m
(
t
)
∣
m
a
x
≤
A
0
|m(t)|_{max} \leq A_0
∣m(t)∣max≤A0
这样就可以使用包络检波的方法恢复原始调制信号,否则就会发生y轴上下混叠,需改用相干解调,失去了AM接受设备要求简单的特性

AM已调信号的频谱由载波分量、上边带和下边带组成(使用对称的双边谱在搬移时产生了两个边带)
B
A
M
=
2
f
H
B_{AM}=2f_H
BAM=2fH
画AM已调信号的原则:先用虚线画信号 A 0 + m ( t ) A_0+m(t) A0+m(t)的波形,再画其关于t轴对称波形,阐明了载波的最大幅度包络边界;然后按照载波原有的频率(周期)将其搬移到两个对称波形之间,幅度按照对称波形的包络起伏
调制效率 η A M = P S P A M \eta_{AM}=\frac{P_S}{P_{AM}} ηAM=PAMPS P S P_S PS为边带功率,最大值为 1 3 \frac{1}{3} 31,效率低
条件及引理:
- 通常假设 m ( t ) ‾ = 0 \overline{m(t)}=0 m(t)=0,时间平均为零
- 信号的平均功率等于其均方值
- c o s 2 w c ( t ) ‾ = 1 2 \overline{cos^2w_c(t)}=\frac{1}{2} cos2wc(t)=21
P
A
M
=
s
A
M
2
(
t
)
‾
=
1
2
[
A
0
2
+
m
2
(
t
)
‾
]
=
P
c
+
P
s
P_{AM}=\overline{s^2_{AM}(t)}=\frac{1}{2}[A_0^2+\overline{m^2(t)}]=P_c+P_s
PAM=sAM2(t)=21[A02+m2(t)]=Pc+Ps
总功率等于载频功率和边带功率之和
AM抗噪声性能–只讨论包络检波
通过包络检波器后的合成包络
E
(
t
)
=
[
A
0
+
m
(
t
)
+
n
c
(
t
)
]
2
+
n
s
(
t
)
2
)
E(t)=\sqrt{[A_0+m(t)+n_c(t)]^2+n_s(t)^2)}
E(t)=[A0+m(t)+nc(t)]2+ns(t)2)
- 大信噪比:
E
(
t
)
=
A
0
+
m
(
t
)
+
n
c
(
t
)
E(t)=A_0+m(t)+n_c(t)
E(t)=A0+m(t)+nc(t) 经过电容器后直流分量
A
0
A_0
A0被消除
S
o
=
m
2
(
t
)
‾
S_o=\overline{m^2(t)}
So=m2(t)
N
o
=
n
c
(
t
)
2
‾
=
n
i
(
t
)
2
‾
=
n
o
B
N_o=\overline{n_c(t)^2}=\overline{n_i(t)^2}=n_oB
No=nc(t)2=ni(t)2=noB
结论 G A M = 2 3 G_{AM}=\frac{2}{3} GAM=32 - 小信噪比:有门限效应(输出信噪比在输入信噪比小于门限值时急剧下降)
DSB–双边带调制
将AM中的直流偏置去除,就消除了频谱中的载频分量,消除了已调信号表达式的载频项,调制效率为1

s
D
S
B
(
t
)
=
m
(
t
)
c
o
s
w
c
t
s_{DSB}(t)=m(t)cosw_ct
sDSB(t)=m(t)coswct
S
D
S
B
(
w
)
=
1
2
[
M
(
w
+
w
c
)
+
M
(
w
−
w
c
)
]
S_{DSB}(w)=\frac{1}{2}[M(w+w_c)+M(w-w_c)]
SDSB(w)=21[M(w+wc)+M(w−wc)]
S
i
(
t
)
=
S
m
2
(
t
)
‾
=
1
2
m
2
(
t
)
S_i(t)=\overline{S_m^2(t)}=\frac{1}{2}m^2(t)
Si(t)=Sm2(t)=21m2(t)
经过相干解调乘上同步载波后恢复出来
m
o
(
t
)
=
1
2
m
(
t
)
m_o(t)=\frac{1}{2}m(t)
mo(t)=21m(t)
则
S
o
(
t
)
=
m
o
2
(
t
)
‾
=
1
4
m
2
(
t
)
‾
S_o(t)=\overline{m_o^2(t)}=\frac{1}{4}\overline{m^2(t)}
So(t)=mo2(t)=41m2(t)
由于高斯窄带噪声
n
i
(
t
)
=
n
c
(
t
)
c
o
s
w
0
t
−
n
s
(
t
)
s
i
n
w
0
t
n_i(t)=n_c(t)cosw_0t-n_s(t)sinw_0t
ni(t)=nc(t)cosw0t−ns(t)sinw0t且窄带噪声及其两个分量的均值相同均为
N
i
N_i
Ni
则同理输出的噪声 n 0 n_0 n0也是其同相分量 n c n_c nc的一半
N
o
=
n
o
2
(
t
)
‾
=
1
4
n
c
2
(
t
)
‾
=
1
4
N
i
N_o=\overline{n_o^2(t)}=\frac{1}{4}\overline{n_c^2(t)}=\frac{1}{4}N_i
No=no2(t)=41nc2(t)=41Ni
而其正交分量
n
i
n_i
ni被抑制掉
所以 G D S B = 2 G_{DSB}=2 GDSB=2
SSB–单边带调制
与DSB相比只传输其上下边带中的一个,节省一半的带宽,
B
S
S
B
=
f
H
B_{SSB}=f_H
BSSB=fH



S
i
=
S
S
S
B
2
(
t
)
‾
=
1
4
m
2
(
t
)
‾
S_i=\overline{S_{SSB}^2(t)}=\frac{1}{4}\overline{m^2(t)}
Si=SSSB2(t)=41m2(t)
由于有两个分量的影响
m
o
(
t
)
=
1
4
m
(
t
)
m_o(t)=\frac{1}{4}m(t)
mo(t)=41m(t)
S
o
=
m
o
2
(
t
)
‾
=
1
16
m
2
(
t
)
‾
S_o=\overline{m_o^2(t)}=\frac{1}{16}\overline{m^2(t)}
So=mo2(t)=161m2(t)
而
N
i
N_i
Ni与
N
o
N_o
No和DSB情况相同
故有
G
S
S
B
=
1
G_{SSB}=1
GSSB=1
但两者的抗噪声能力相同(相同带宽)
VSB–残留边带调制
这里以DSB信号通过滤波器为例

VSB滤波器需满足的条件(载频处互补对称)
H
(
w
+
w
c
)
+
H
(
w
−
w
c
)
=
c
o
n
s
t
H(w+w_c)+H(w-w_c)=const
H(w+wc)+H(w−wc)=const
已调信号的带宽
f
H
<
B
V
S
B
<
2
f
H
f_H<B_{VSB}<2f_H
fH<BVSB<2fH
非线性调制(角度调制)
s
m
(
t
)
=
A
c
o
s
(
w
c
t
+
ϕ
(
t
)
)
s_m(t)=Acos(w_ct+\phi (t))
sm(t)=Acos(wct+ϕ(t))
ϕ
(
t
)
\phi (t)
ϕ(t)称作瞬时相位偏移(相对于载波相位
w
c
t
w_ct
wct)
d ϕ ( t ) d t \frac{d\phi(t)}{dt} dtdϕ(t)陈作瞬时频偏(相对于载频 w c w_c wc),这里用到了瞬时相位对时间求导得到瞬时频率
与线性调制相比:
- 较高的抗噪声性能
- 占用更宽的带宽
PM–调相
瞬时相位偏移随调制信号线性变化
S
P
M
(
t
)
=
A
c
o
s
(
w
c
(
t
)
+
K
p
m
(
t
)
)
S_{PM}(t)=Acos(w_c(t)+K_pm(t))
SPM(t)=Acos(wc(t)+Kpm(t))调相灵敏度
K
p
(
r
a
d
/
V
)
K_p(rad/V)
Kp(rad/V)
调相系数 m p = K p A m m_p=K_pA_m mp=KpAm
FM–调频
瞬时频率偏移随调制信号线性变化(瞬时相位偏移随信号积分线性变化)
S
F
M
(
t
)
=
A
c
o
s
(
w
c
(
t
)
+
K
f
∫
m
(
λ
)
d
λ
)
=
A
c
o
s
[
w
c
(
t
)
+
K
f
A
m
∫
c
o
s
w
m
τ
d
τ
]
=
A
c
o
s
[
w
c
(
t
)
+
K
f
A
m
w
m
s
i
n
w
m
t
]
\begin{aligned}S_{FM}(t)&=Acos(w_c(t)+K_f\int m(\lambda)d\lambda)\\&=Acos[w_c(t)+K_fA_m\int cosw_m\tau d\tau]\\&=Acos[w_c(t)+\frac{K_fA_m}{w_m}sinw_mt]\\\end{aligned}
SFM(t)=Acos(wc(t)+Kf∫m(λ)dλ)=Acos[wc(t)+KfAm∫coswmτdτ]=Acos[wc(t)+wmKfAmsinwmt]调相灵敏度
K
f
(
r
a
d
/
(
V
⋅
s
)
K_f(rad/(V\cdot s)
Kf(rad/(V⋅s)
调频系数 m f = K f A m w m = Δ w w m = Δ f f m m_f=\frac{K_fA_m}{w_m}=\frac{\Delta w}{w_m}=\frac{\Delta f}{f_m} mf=wmKfAm=wmΔw=fmΔf Δ f \Delta f Δf为最大频偏, f m f_m fm相邻变频间隔
带宽(卡森公式,工程近似) B F M = 2 ( m f + 1 ) f m = 2 ( Δ f + f m ) B_{FM}=2(m_f+1)f_m=2(\Delta f+f_m) BFM=2(mf+1)fm=2(Δf+fm)
调频信号的产生:直接调频和间接调频(NBFM-WBFM)
调频信号的解调:
- 非相干解调(NBFM和WBFM)
- 相干解调(NBFM)
调制后总功率不变,功率分配比例与 m f m_f mf有关
输出信噪比(大信噪比)
S
o
N
o
=
3
2
m
f
2
A
2
/
2
n
o
f
m
\frac{S_o}{N_o}=\frac{3}{2}m^2_f\frac{A^2/2}{n_of_m}
NoSo=23mf2nofmA2/2
制度增益
G
F
M
=
3
m
f
2
(
m
f
+
1
)
G_{FM}=3m_f^2(m_f+1)
GFM=3mf2(mf+1)
输出信噪比与调幅信号相比为其
3
m
f
2
3m^2_f
3mf2倍

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容





所有评论(0)