引言

机器人的动力学方程通常可以通过牛顿-欧拉公式或拉格朗日动力学公式得到。

关于机器人动力学是什么，可以参考Robitics公众号的这一系列文章干货 | 机械臂的动力学（二）：拉格朗日法；或者在CSDN上找，资料很多，如机器人动力学——拉格朗日法

——简单来说，牛顿-欧拉公式通过力学分析得到运动方程，而拉格朗日动力学公式从能量角度得到运动方程。

Q：什么是运动方程？
A：百度上的解答为：“运动方程是描述结构中力与位移(包括速度和加速度)关系的数学表达式。现在的各种模型，通常为多输入多输出形式，一种比较合适的建模方式是通过状态空间进行建模。
在分析时，常常以广义位置【位移、角度】、广义速度【速度，角速度】为状态向量$x$；$\dot{x}$自然而然牵扯到广义加速度【加速度，角加速度】；
此外，这类建模中输入向量$u$通常为力矩【移动副】或者扭矩【转动副】
因此，运动方程常常是广义加速度、广义速度、广义位置和输入向量之间的关系等式组

---

本文将简单介绍拉格朗日动力学建模过程，并以一阶倒立摆建模过程为例，手推运动方程，并在matlab借助代码验证该过程。

拉格朗日方程

拉格朗日量$\mathcal{L}$可以用以下公式表示：

$\mathcal{L}(\mathrm{q},\dot{\mathrm{q}})=\mathcal{T}(\mathrm{q},\dot{\mathrm{q}})-\mathcal{V}(\mathrm{q})$，其中$\mathcal{T}$为系统动能、$\mathcal{V}$为系统势能。

哈狗恩朗日公式法可以用以下公式表示
$$\begin{array}{l}\frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial {\dot{q}}_j}\right)-\frac{\partial \mathcal{L}}{\partial q_j}=f\end{array}$$

这个方程也称为含外力的欧拉-拉格朗日方程（在标准形式的欧拉-拉格朗日方程中，外力 $f$ 等于零）

Q：零势能面怎么选择呢？是以水平方向为零重力势能吗？

——零势能面不影响最终答案，相当于势能$\mathcal{V}$加了一个不随时间变化的常数

此外【这部分内容笔者并没有找到太好的资料，有待补充，同时也欢迎大家在评论区分享自己找到的的资料】
根据系统的串并联结构，可划分第一类拉格朗日方程和第二类拉格朗日方程

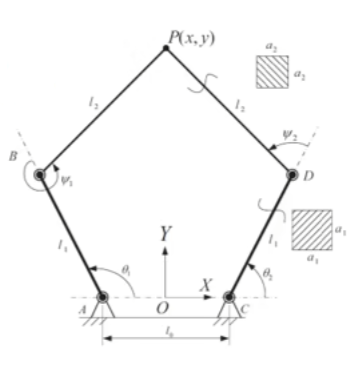
• 第一类：$\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{\mathbf{q}}}\right)-\frac{\partial \mathcal{L}}{\partial \mathbf{q}}+{\mathbf{\Phi }}_{\mathbf{q}}^T\lambda ={\mathbf{Q}}_{ex}$，适用于闭环结构，即并联机构
  如双足模型中常用的五连杆模型或者七连杆模型
  
  如图所示的P点不仅会被A影响，也会被C影响
  
• 第二类：$\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial \mathcal{L}}{\partial \dot{\mathbf{q}}}\right)-\frac{\partial \mathcal{L}}{\partial \mathbf{q}}={\mathbf{Q}}_{ex}$适用于开环结构，即串联机构，本文讨论的就是串联机构

一阶倒立摆的建模

物理模型

变量声明

物理量	符号
滑块质量	$M$
摆杆质量	$m$
摆杆转动轴心到杆质心长度【半杆长】	$l$
摆杆在转轴处转动惯量	$J$
小车受到外力	$F$
小车位置	$x$
摆杆与竖直方向夹角【本文顺时针为正】	$\theta$

力学分析

对滑块分析：$$\begin{array}{l}M\ddot{x}=F-F_x\end{array}\text{\hspace{1em}(1)}$$
对杆分析：
$$\{\begin{array}{l}\text{ x向: }{F}_x=m\frac{d^2}{d{t}^2}\left(x+l\sin \theta \right)\\ \\ \text{ y向: }{F}_y-mg=m\frac{d^2}{d{t}^2}\left(l\cos \theta \right)\\ \\ \text{力矩: }{F}_{y}l\sin \theta -F_{x}l\cos \theta =J\ddot{\theta }\end{array}\text{\hspace{1em}(2)}$$

公式推导

$$\begin{array}{l}x向\to F_x=m\ddot{x}+ml\left(\cos \theta \cdot \ddot{\theta }-\sin \theta \cdot {\dot{\theta }}^2\right)\end{array}\text{\hspace{1em}(3)}$$
$$\begin{array}{l}y向\to F_y=mg-ml\left[\sin \theta \cdot \ddot{\theta }+\cos \theta \cdot {\dot{\theta }}^2\right]\end{array}\text{\hspace{1em}(4)}$$

带入力矩式，
$$\begin{array}{l}(mgl\sin \theta -m{l}^2{\sin }^2\theta \cdot \ddot{\theta }-m{l}^2\sin \theta \cos \theta \cdot {\dot{\theta }}^2)-(ml\cos \theta \cdot \ddot{x}+m{l}^2{\cos }^2\theta \cdot \ddot{\theta }-m{l}^2\cos \theta \sin \theta \cdot {\dot{\theta }}^2)=J\ddot{\theta }\end{array}\text{\hspace{1em}(5)}$$

运行结果

利用${\sin }^2\theta +{\cos }^2\theta =1$，有：
$$\begin{array}{l}mgl\sin \theta -ml\cos \theta \cdot \ddot{x}=(J+m{l}^2)\cdot \ddot{\theta }\end{array}\text{\hspace{1em}(6)}$$

另外，将(3)代入(1)，有
$$\begin{array}{l}\\ -ml\sin \theta \cdot {\dot{\theta }}^2+ml\cos \theta \cdot \ddot{\theta }+(M+m)\cdot \ddot{x}=F\end{array}\text{\hspace{1em}(7)}$$

拉格朗日法建模

系统动能由滑块动能$T_1$和摆杆动能$T_2$构成
滑块纯滑动
$$T_1=\frac{1}{2}\ast M\ast v^2,v=\frac{d}{dt}x$$
摆杆滑动+摆动
$$T_2=\frac{1}{2}\ast m\ast v^2,v=\frac{d}{dt}p$$
其中$p$点坐标为$p=(s+\frac{l}{2}\sin \theta ,\frac{l}{2}\cos \theta )$

---

重力势能
$$V=m\ast g\ast 1/2\ast l\ast \cos \theta$$

构造matlab代码

clear all
syms g M m l s(t) J theta(t) F(t)

T1 = 1/2*M*diff(s,t)^2;
T2 = 1/2*J*diff(theta,t)^2 + 1/2*m*(diff(s+1/2*l*sin(theta),t)^2 + diff(1/2*l*cos(theta),t)^2);
V = m*g*1/2*l*cos(theta);
L = T1 +T2 - V;
eqn = functionalDerivative(L,[s;theta]) == [-F;0]
eqn = simplify(eqn)

【若报错注意看看是不是下载matlab时没有下载对应组件，按照当时的Matlab安装流程重新安装】

运行结果

附：上文的(6) (7)
$$\{\begin{array}{l}mgl\sin \theta -ml\cos \theta \cdot \ddot{x}=(J+m{l}^2)\cdot \ddot{\theta }\\ \\ -ml\sin \theta \cdot {\dot{\theta }}^2+ml\cos \theta \cdot \ddot{\theta }+(M+m)\cdot \ddot{x}=F\end{array}$$
二者表达等价

至此，拉格朗日建模过程已经实现，以下是一个完整的例子。

拉格朗日法+设置初值求系统中变量

如题所示为弹簧-滑块模型，表面光滑

• 设置初值：若弹簧一开始有伸长量$d{x}_0$或者物块一开始有速度$v_0$，则可以求出物块距离初值位置随时间的表达式
  设弹簧原长为$x_0$【不重要】，在Matlab中可根据初始伸长量和速度求得x的表达式【此时的x事实上是dx，代表弹簧伸长量】

clear all
x0 = 10
syms m k x(t)
T = 1/2*m*diff((x+x0), t)^2;
V = 1/2*k*x^2;
L = T - V;
eqn = functionalDerivative(L, x) == 0
assume(m, "positive")
assume(k, "positive")
Dx(t) = diff(x(t), t);
xSol = dsolve(eqn, [x(0) == 11, Dx(0) == 7])

• 运行结果如下
  
• 验证环节
  知识储备不足，不会验证。。。
  能想到的方法就是利用能量关系列出与x有关的方程式并求解，实现过程与此方法完全一致。

我还没摸清楚这种方法在多维变量（多输入多输出【尤其是多输入】）时怎么使用，它的求解思路以及原理尚不清楚，有待探究

---

多输入时，报错如下：

写在后面

• Matlab中的functionalDerivative函数应该只是一个求微分方程的函数，然后 拉格朗日动力学方程 是写成了微分方程形式的函数，因此可以用这个函数求解
• 这个函数的泛用性应该很强

参考文献

本文的部分方法及代码来自B站视频教程LQR倒立摆 从建模到控制 零基础都能复现，推荐观看！