|●梯度下降是什么|●梯度下降算法原理|●梯度下降实例
《老饼讲解机器学习》本文讲解机器学习中最经典基础的梯度下降算法。
《老饼讲解机器学习》--一个经典的机器学习算法网站 https://www.bbbdata.com/text/18
https://www.bbbdata.com/text/18
目录
本文讲解机器学习中最经典基础的梯度下降算法。
梯度下降法算是一种求解最小值的算法,机器学习中经常使用,因为机器学习中通常需要求最小化损失函数时的参数的取值。
这里我们介绍梯度下降算法的思想、实现流程和优缺点。
梯度下降的手算过程和代码实现见文章:《梯度下降算法实例与代码》
一、问题背景
在单变量函数求取最小值问题中,我们通常只要令f(x)的导数为0,然后解出x就可以。
在多元函数中,求偏导令偏导为0,解出x是非常困难的,
虽然n个自变量,能求得n条偏导等式。然而,只有这n条等式是线性方程组时,我们才有系统的方法对其求解。如果是非线性方程,我们目前并没有成熟的求解方案。Pass:这也是为什么我们很喜欢构造线性问题,因为它能轻松求解。
所以,联立偏导方程求精确解的路子行不通,我们的替代方案就是进行数值求解,梯度下降法就是其中常用方法之一。
二、梯度下降算法思路
(一) 思路概览
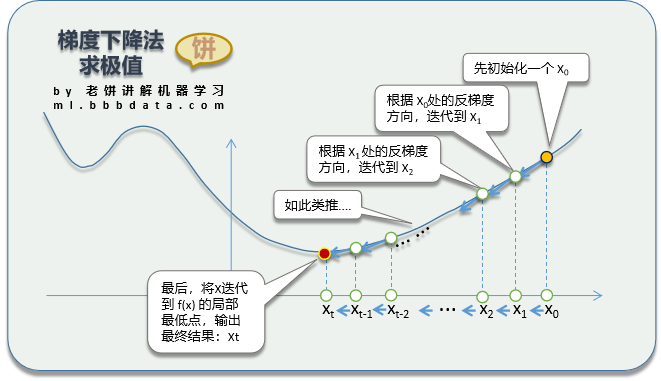
梯度下降算法的思路是,
先取一个初始值x0,然后进行迭代。
每次都往梯度的反方向调整(在一维中即导数的负方向)它。
直到迭代条件终止(例如无法令f(x)的值下降,即达到局部最低点)。
(二) 关于梯度
在一元函数中,负梯度就是导数的反方向。
在多元函数中,负梯度就是各个变量偏导数的反方向。
它是函数下降最快的方向(即调整相同步长,负梯度能令f(x)下降最快),故也称为最速下降法。
(三) 关于初始值
从算法原理,我们可以知道,梯度下降法对 x 的初始化非常敏感,因为它只能找到离初始值最近的局部极小值,如果初始化不好,找到的结果也不好。
往往是先随机初始化,然后多跑几次,看哪个结果好,就用哪一个。
三、算法流程
1.先初始化x的值
(按个人经验初始化,或随机初始化,或设为0)
2.计算在
处的梯度
,令
,(lr为学习率,可设为0.1)
3.计算在
处的梯度
,令
,
4....如此类推....一直到满足停止迭代条件(达到迭代次数,或者与
变化不大,或者
与
变化不大),最后的
即为所要找的解。
简单的说,就是先初始化,然后按
不断迭代就行
四.实例演示
(一) 问题
求
为何值时,
取得最小值。( 易知道,y的最小值在
=2,
处取得,为0.)
下面展示用梯度下降法寻找解的具体过程,看结果是否与我们预期一致。
(二) 算法实际操作过程
第40次迭代时,dx1与dx2都极小,我们退出迭代 ,
以
作为最终结果,此时函数值 2.2969011842121404e-07
与预期的 x= [2,3] , y=0 几乎一致。
(三) 代码实现
上例 python程序如下:
# -*- coding: utf-8 -*- """ 梯度下降求y= (x1-2)^2+(x2-3)^2的最小解 """ x1 = 0 # 初始化x1 x2 = 0 # 初始化x2 for i in range(100): #------计算梯度-------- dx1 = 2*x1-4 dx2 = 2*x2-6 #----- 往负梯度方向更新x------ x1 = x1 - 0.1*dx1 x2 = x2 - 0.1*dx2 #----- 如果梯度过小,则退出迭代 --------if((abs(dx1)< 0.001) & (abs(dx2)< 0.001)):break print("第"+str(i+1)+"轮迭代:x=:["+str(x1)+","+str(x2)+"],y="+str((x1-2)**2+(x2-3)**2))结果:
第1轮迭代:x=:[0.4,0.6000000000000001],y=8.32 第2轮迭代:x=:[0.7200000000000001,1.08],y=5.3248 第3轮迭代:x=:[0.976,1.464],y=3.4078720000000002 .................. 第39轮迭代:x=:[1.9996676930010537,2.9995015395015807],y=3.588908100330732e-07 第40轮迭代:x=:[1.999734154400843,2.9996012316012646],y=2.2969011842121404e-07
五.算法的拓展理解
1.为什么按负梯度下降
《数学分析》中,负梯度方向是函数下降最快的方向,即x=[2,3],如果梯度为[1,2],则x往[1,2]方向调整,能令函数f(x)下降最快的方向(所谓最快,即调整同样的步长,该方向能令函数下降最快)
按负梯度下降,保证了调整方向的正确性。
2.为什么要设置学习率
目的是为了保证按梯度方向调整一定能下降。
梯度方向能下降是瞬时的,如果调整步长过大,则不一定能保证函数能下降,但只要调整步长足够小,函数就能下降(前提是梯度不为0)。
所以,我们在调整时,加入学习率lr,以控制步长:
3、学习率的设置与自适应学习率
要保证能下降,学习率就不能过大,但学习率很小,每次迭代调整都很小,就需要迭代很多次。
为此,我们可以设定一个较中肯的学习率(例如,lr = 0.1)。
如果更智能一些,在程序中把学习率改为自适应学习率: 函数能下降,我们把学习率调大些,如果函数本次迭代不能下降,我们就把学习率调小些。
或者更智能的设置,这就属于梯度下降法的拓展了。
总的来说,
(1)按负梯度调整,加上学习率的控制,则能保证x的调整,函数一定能下降。
(2)按负梯度下降,由于负梯度是下降最快的方向,在下降速度上更加有效。
六.梯度下降法的弊端
(1) 遇到局部最优时,算法就停止,因为此时梯度为0。因此,该算法只能找到初始解x_0的局部最优,对跳出局部完全无反抗能力。
(2) 要求函数是连续的(可求偏导)
七.梯度下降算法的代码实现
梯度下降算法的代码实现如下:
# -*- coding: utf-8 -*-
"""
梯度下降求y= (x1-2)^2+(x2-3)^2的最小解
"""
x1 = 0 # 初始化x1
x2 = 0 # 初始化x2
for i in range(100):
#------计算梯度--------
dx1 = 2*x1-4
dx2 = 2*x2-6
#----- 往负梯度方向更新x------
x1 = x1 - 0.1*dx1
x2 = x2 - 0.1*dx2
#----- 如果梯度过小,则退出迭代 --------
if((abs(dx1)< 0.001) & (abs(dx2)< 0.001)):break
print("第"+str(i+1)+"轮迭代:x=:["+str(x1)+","+str(x2)+"],y="+str((x1-2)**2+(x2-3)**2))相关文章

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容











所有评论(0)