最短路径与关键路径
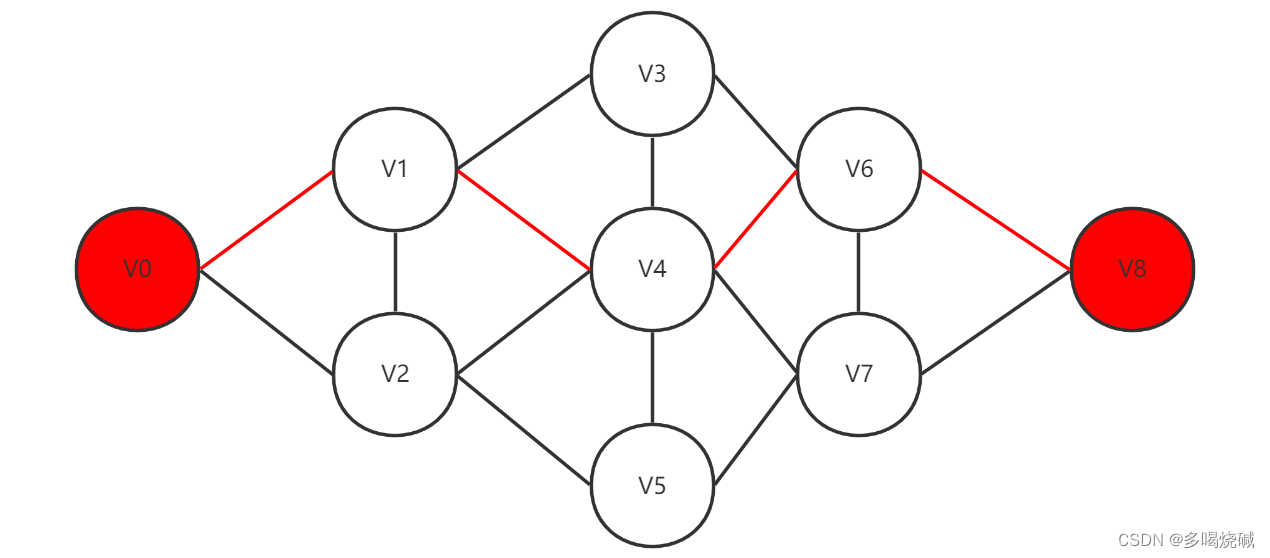
好久没更新了,过完年啦,现在更新一下叭路径起始的第一个顶点称为源点,最后一个顶点称为终点。图下图中,我们用红色标注出的就可以认为是一个路径(V0 ->V1 ->V4 ->V6 ->V8)的源点和终点,但不要有误区,其实图中的任何一个顶点都可作为源点或者终点,源点与终点只是相对一条路径而言的对于无向图而言,从源点V0到终点V8的最短路径就是从源点V0到终点V8所包含的边最少的路径.我们只需要从源点V
目录
前言
好久没更新了,过完年啦,现在更新一下叭
一.最短路径
1.基本概念
1.1什么是源点?
路径起始的第一个顶点称为源点,最后一个顶点称为终点。图下图中,我们用红色标注出的就可以认为是一个路径(V0 ->V1 ->V4 ->V6 ->V8)的源点和终点,但不要有误区,其实图中的任何一个顶点都可作为源点或者终点,源点与终点只是相对一条路径而言的

1.2什么是最短路径
对于无向图而言,从源点V0到终点V8的最短路径就是从源点V0到终点V8所包含的边最少的路径.我们只需要从源点V0出发对图做广度优先搜索,一旦遇到终点V8就终止。我们可以具体来看看如何得到无向图中源点V0到终点V8的最短路径。
第一步:遍历顶点V0:

第二步:遍历顶点V0的邻接顶点V1和V2(具体操作中我们使用队列来进行实现):

第三步:遍历顶点V1的邻接顶点V3和V4,遍历顶点V2的邻接顶点V5 :

第四步:遍历顶点V3的邻接顶点V6和V4的邻接顶点V7:

第五步:遍历顶点V6的邻接顶点V8,发现正好是终点

由此可以得到,图中从源点V0到终点V8的(第一条)一条最短路径 (V0 ->V1 ->V3 ->V6 ->V8 )。
2.作用
简单来说,我们要从大兴机场到北京天安门,如何规划路线才能换乘最少,并且耗时最少呢?这时候,最短路径算法就派上用场了,你每天使用的导航系统进行道路规划也同样依赖于底层的算法!虽然现实情况可能更复杂一些,但是学习最基础的算法对于我们日后的提升总有莫大的帮助。
3.迪杰斯特拉算法
迪杰斯特拉算法是一个单源点的一个最短路径算法,也就是说,我们这个算法会求得从一个顶点到其所有顶点的最短路径。
首先,引入一个辅助变量D,它的每一个分量D[i]表示当前所找到的从源点v到每一个顶点Vi的最短路径的长度,它的初始状态为:若从V到Vi有弧,则D[i]为弧上的权值。否则D[i]为无穷大。显然,长度就为:的路径就是从 v 出发的长度最短的一条最短路径。此路径为(V,Vj) 。我们直接看例子,以下图为例:

第一步:初始化辅助向量D,路径向量P 和 当前已求得顶点V0到Vj的最短路径的向量Final。

辅助向量D的初态为:若从V0到Vj有弧,则D[j]为弧上的权值;否则D[j]为无穷大。对应到图中,V0到V1有弧,则D[1] = 1 ;V0 到V2有弧,则D[2] = 5 ; 到其他顶点没有弧,则相应的用无穷表示。路径向量P用于存储最短路径下标的数组,初始时全部置为零;向量Final中值为1表示顶点V0到Vj的最短路径已求得,V0到V0的最短路径当然是已求得,所以将Final[V0]设置为1。接下来就是迪杰斯特拉算法的核心了。
第二步:遍历源点V0, 找到源点V0的邻接顶点中距离最短的顶点,即V1, V0到V1的最短路径为1已经求出,更新Final[1] = 1

第三步:遍历顶点 V1,找到顶点V1的邻接顶点V0 、V2 、V3 、V4 (其中V0已经遍历过了,不需要考虑)。从V1到V2的距离是 3,所以V0到V2的距离是 1+3=4,小于辅助向量D中的距离 5,则更新 D[2] = 4;从V1到V3的距离是 7,所以V0到 V3 的距离是 1+7=8,小于辅助向量中的D[3],则更新D[3] = 8 ;从V1到V4的距离是 5,所以V0到V4的距离是 1+5=6,小于辅助向量中的D[4] ,则更新D[4] =6;相应的将顶点V2 、V3 、V4 的前驱结点更新为V1的下标 1。

接下来就是重复第二步、第三步
第四步:遍历源点 V0, 找到从源点V0出发距离最短的且final=0的顶点,发现为 V2, 更新Final[2] = 1

第五步:遍历顶点V2并更新辅助向量 D 和 路径向量 P 。

第六步:找到从源点V0出发距离最短的且final=0的顶点,发现为V4 , 更新final[4] = 1

第七步:遍历顶点V4并更新辅助向量D和路径向量P

第八步:找到从源点V0出发距离最短的且final=0的顶点,发现为 V3 , 更新 Final[3] = 1.

第九步:遍历顶点V3并更新辅助向量 D 和 路径向量 P

第十步:找到从源点V0出发距离最短的且final=0的顶点,发现为V5 , 更新final[5] = 1

第十一步:遍历顶点 V5 并更新辅助向量 D 和 路径向量 P

第十二步:找到从源点 V0出发距离最短的且final=0的顶点,发现为 V6 , 更新 final[6] = 1

第十三步:遍历顶点V6并更新辅助向量 D 和 路径向量 P

第十四步:找到从源点 V0出发距离最短的且final=0的顶点,发现为 V7 , 更新 final[7] = 1

第十五步:遍历顶点 V7 并更新辅助向量 D 和 路径向量 P

第十六步:找到从源点 V0出发距离最短的且final=0的顶点,发现为 V8 , 更新 final[8] = 1 .此时,全部结点完毕,算法结束

根据路径向量我们则可以得到从源点V0到终点V8的最短路径

#include<stdio.h>
#include<stdlib.h>
#define INF 65535
//基于带权无向图 ----O(|v|^2)
int g[105][105],flag[105],dist[105],path[105],nv,ne,s,end;
void dujkstra(){
int minn,k;//最小的dist值 最小的dist值的点的下标
//初始化dist path
for(int i=0;i<nv;i++){
dist[i]=INF;
path[i]=-1;
}
//确定起点自己到自己的最短路径
flag[s]=1;
dist[s]=0;
for(int j=0;j<nv;j++){
if(flag[j]==0&&g[s][j]!=INF&&dist[j]>(dist[s]+g[s][j]))
{
dist[j]=dist[s]+g[s][j];
path[j]=s;
}
}
//确定其他点的最短路径
for(int i=1;i<nv;i++){
minn=INF;
for(int j=0;j<nv;j++){
if(flag[j]==0&&dist[j]<minn){
minn=dist[j];
k=j;
}
}
flag[k]=1;
for(int j=0;j<nv;j++){
if(flag[j]==0&&g[k][j]!=INF&&dist[j]>(dist[k]+g[k][j]))
{
dist[j]=dist[k]+g[k][j];
path[j]=k;
}
}
}
}
int main()
{
int x,y,w;
scanf("%d %d",&nv,&ne);
scanf("%d %d",&s,&end);
// 初始化邻接矩阵
for(int i=0;i<nv;i++)
for(int j=0;j<nv;j++)
{
if(i==j)g[i][j]=g[j][i]=0;
else g[i][j]=g[j][i]=INF;
}
//建图
for(int i=0;i<ne;i++)
{
scanf("%d %d %d",&x,&y,&w);
g[x][y]=g[y][x]=w;
}
dijkstra();
printf("起点%d 到 终点%d 的最短路径的权值和为:%d\n最短路径如下:",s,end,dist[end]);
printf("%d",end);
int p=end;
while(path[p]!=-1)
{
printf("->%d",path[p]);
p=path[p];
}
return 0;
}4. 弗洛伊德算法
对于迪杰斯特拉算法中谈到的是如何解决图中任意两个顶点之间最短路径的计算问题,迪杰斯特拉算法可以计算指定顶点到其他顶点之间的最短路径,那么我就可以通过指定网络中的每一个顶点为源点,重复执行迪杰斯特拉算法 n 次,这样便可以得到每一对顶点之间的最短路径,显然这种方式的时间复杂度为O(n^3) 。Floyd算法时间复杂度也为O(n^3) ,但是她的实现比那种方式更加简洁优雅,重要的是思想也很巧妙,她就是弗洛伊德(Floyd)算法
迪杰斯特拉算法计算指定顶点到其他顶点之间的最短路径需要维护一个长度为 n 的辅助向量D。而弗洛伊德算法既然可以求得每一对顶点之间的最短路径,自然要维护一个n*n 的二维辅助向量D,同理也需要维护一个 nn 的二维路径向量 P。接下来你所看到的就是弗洛伊德算法最核心的部分了。现定义一个 n 阶方阵序列:

其中:

我们图的邻接矩阵 : D(-1)
表示从顶点Vi到顶点Vj的中间顶点的序号不大于 1 的最短路径的长度; D(1)[i][j]
表示从顶点Vi到顶点Vj的中间顶点的序号不大于 k 的最短路径的长度; D(k)[i][j]
表示从顶点Vi到顶点Vj的最短路径的长度; D(n-1)[i][j]D(k)[i][j]
接下来,让我们愉快的来看例子:

我们先以上面包含三个顶点个无向图来讲解弗洛伊德算法的思想,然后再使用在将迪杰斯特拉算法时用到的图上人脑模拟一遍
图中包含三个顶点的邻接矩阵的右上角标注的是 D^0,这是为什么呢?不是说好的 n 阶方阵初始化为图的邻接矩阵吗? 这就得感慨数学的严谨性质了,除 n 阶方阵D^(-1)之外,其他任何一个 n 阶方阵都可以使用它的前一个状态获得,则
![]()
故 n 阶矩阵D^-1和D^0是同一个矩阵。那么D^1如何求得呢?当然是用她的前一个状态D^0求得了
![]()
比如计算顶点V0到V2的最短路径:
![]()
其中
![]()
的值为5,即顶点V0到顶点V2的直接距离为 5;而

表示顶点V0到顶点V2经顶点V1中转以后的距离为4,从而将
![]()
更新为4,表示顶点V0到顶点V2的最短路径为4。
这就是弗洛伊德算法的精妙所在,在一个图中,要求得任意两个顶点Vi和Vj之间的最短路径,我们则可以通过两个顶点Vi和Vj之间的顶点进行中转,对于算法本身而言,则是不断得尝试所有的中转结点,从而确定两个顶点之间的最短路径。
根据公式计算完之后,获得 n 阶矩阵D^1

4.1过程演示
为了更清楚弗洛伊德算法的执行过程,和弗洛伊德算法的精妙所在,我们以下图为例,一步一步得脑子过一遍。
依旧用之前的图

算法第一步,初始化 n 阶矩阵 D(辅助向量) 和n 阶矩阵P(路径向量):

第二步:k == 1,此时

我们主要就是计算![]()
其中
就是下方我们所标记的绿色列,而![]()
则表示我们所标记的绿色行。
这样我想大家就可以进行轻松计算了,我们以取 i == 0 为例进行计算,则![]()
分别与![]()
所表示的绿色行中的每一个元素进行相加,即得到 [2,1,4,8,6,1+∞,1+∞,1+∞,1+∞],然后与V0的行[0,1,5,∞,∞,∞,∞,∞,∞] 进行大小比较,将更小值保留,即得到 D(1)
中的V0行;此时相应的只要将![]()
更新为
红色表示被更新过的元素

第三步:k == 2,![]()
表示绿色一列![]()
表示绿色的行。
0 <= i <= 8,分别与
表示的绿色行进行运算并比较更新,获得 D^2.

第四步:k == 3,
表示绿色一列,![]()
表示绿色的行。0 <= i <= 8,分别与表示的绿色行进行运算并比较更新,从而获得 D^3.

第五步:k == 4,![]()
表示绿色一列,![]()
表示绿色的行。
0 <= i <= 8,分别与![]()
表示的绿色行进行运算并比较更新,从而获得D^4

第六步:k == 5,![]()
表示绿色一列,![]()
表示绿色的行。
0 <= i <= 8,分别与![]()
表示的绿色行进行运算并比较更新,从而获得D^5.

第七步:k == 6,![]()
表示绿色一列,
表示绿色的行。
0 <= i <= 8,分别与![]()
表示的绿色行进行运算并比较更新,从而获得D^6.

第八步:k == 7,![]()
表示绿色一列,![]()
表示绿色的行。
0 <= i <= 8,分别与![]()
表示的绿色行进行运算并比较更新,从而获得D^7.

第九步:k == 8,同样的道理进行计算,我们注意到绿色区域划分出的左上角的区域都是不需要被更新的,绿色区域本身也是不更新的,所以 D^7与D^8 是一样的了

这样,整个弗洛伊德算法的执行过程就结束了,我知道看完,可能还是有一点模糊,不过我希望你能多看几遍这个例子,最好是自己也和给你们绘制的图一样,自己手工地人脑模拟一遍,只有这样,你才会真正理解算法的精妙所在
二.拓扑排序
1.基本概念
1.1什么是有向无环图
一个无环的有向图称为有向无环图,简称 DAG 图。直接看图

图中最左边的是有向树,中间的是有向无环图,最右则的是有向图(因为图中BED三个顶点之间构成一个有向环)
1.2什么是活动
所有的工程或者某种流程都可以分为若干个小的工程或者阶段,我们称这些小的工程或阶段为“活动”。打个比方,如何把一只大象装到冰箱里,很简单,分三步。第一,打开冰箱门;第二,将大象装进去;第三,关上冰箱门。这三步中的每一步便是一个 “活动”
1.3什么是AOV网
在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系的有向图称为顶点表示活动的网,简称AOV网。
日常生活中,一项大的工程可以看作是由若干个子工程组成的集合,这些子工程之间必定存在一定的先后顺序,即某些子工程必须在其他的一些子工程完成后才能开始。
AOV网中的弧表示活动之间存在的某种制约关系,比如上面说到将大象装入冰箱,必须先打开冰箱门,才能将大象装进去,大象装进去才能关上冰箱门,从而完成我们的任务。还有一个经典的例子那就是选课,通常我们是学了C语言程序设计,才能学习数据结构,这里的制约关系就是课程之间的优先关系。
1.4什么是拓扑序列
设G=(V,E)是一个具有n个顶点的有向图,V中的顶点序列 V1,V2,V3.......Vn满足若从顶点Vi到Vj有一条路径,则在顶点序列中顶点Vi必在顶点Vj之前。则我们称这样的顶点序列为一个拓扑序列
1.5什么是拓扑排序
所以说,所谓的拓扑排序,其实就是对一个有向无环图构造拓扑序列的过程。当然这里的说法不够正式,也是为了理解方便,拓扑排序的官方定义是这样的:
由某个集合上的一个偏序得到该集合上的一个全序的操作过程称为拓扑排序。
2.算法思想
拓扑排序的算法步骤很简单,就是两步:
(1) 在有向图中选一个没有前驱的顶点且输出之。
(2) 从图中删除该顶点和所有以它为尾的弧。
重复上述两步,直至全部顶点均已输出,或者当前图不存在无前驱的顶点为止,后一种情况说明有向图中存在环。
为了清楚地理解拓扑排序思想,我们分别采用有向无环图和有向有环图进行举例说明。
2.1有向无环图

第一步:在有向图中选择一个没有前驱的顶点并输出;观察图中的顶点,发现顶点V1和顶点V6都是没有前驱的顶。假设我们先输出顶点V1(当然也可以先输出V6,从此处也就可以看出拓扑序列可以有多个)

第二步:从图中删除顶点V1和所有以它为尾的弧

之后的步骤就是重复一二两步,我们接着看。
第三步:在有向图中选择一个没有前驱的顶点并输出;图中没有前驱的顶点为V6和顶点V3(同样的道理,我们可以选择这两个顶点的任何一个,假设我们选择顶点V6)

第四步:删除顶点V6和所有以它为尾的弧

第五步:在有向图中选择一个没有前驱的顶点并输出;图中没有前驱的顶点为V4和顶点V3(同样的道理,我们可以选择这两个顶点的任何一个,假设我们选择了顶点V4)。删除顶点V4和所有以它为尾的弧

重复操作:在有向图中选择一个没有前驱的顶点并输出;图中没有前驱的顶点为V3。删除顶点V3和所有以它为尾的弧


在有向图中选择一个没有前驱的顶点并输出;图中没有前驱的顶点为V2和 V5(同样的道理,我们可以选择这两个顶点的任何一个,假设我们选择了顶点V2 ) 。删除顶点V2和所有以它为尾的弧

在有向图中选择一个没有前驱的顶点并输出;图中没有前驱的顶点为V5,选择并输出,此时所有的顶点均已经输出,算法结束,我们就得到了下图中的一个拓扑序列 ,整个过程便叫做拓扑排序
2.2有向有环图
其实过程和之前类似,只是给大家提供一个思路,如果面试官问你,如何判断一个有向图中是否存在环时,你应该第一反应想到的就是拓扑排序,为什么拓扑排序可以判断一个有向图中是否存在环呢?

第一步:在有向图中选择一个没有前驱的顶点并输出;图中没有前驱的顶点为A。删除顶点A和所有以它为尾的弧

第二步:在有向图中选择一个没有前驱的顶点并输出;图中没有前驱的顶点为C。删除顶点C和所有以它为尾的弧

第三步:在有向图中选择一个没有前驱的顶点并输出;发现当前图不存在无前驱的顶点,但拓扑序列中并未输出所有的顶点,所以剩下的顶点构成了环,也证明了该有向图存在环
3.思想的实现
针对于拓扑排序思想篇提到的两步操作,我们采用邻接表作为有向图的存储结构,并且在头结点中增加一个存放顶点入度的数组。入度为零的顶点即为没有前驱的顶点,删除顶点及以它为尾的弧的操作,则可换以弧头顶点的入度减1来实现。
为了避免重复检查入度为零的顶点,可另设一个栈暂存所有入度为领的顶点。
为了清晰地呈现拓扑排序的实现,我们还是以上面提到的有向无环图为例子进行讲解。
图的邻接表表示

第一步:遍历所有顶点,将入度为0的顶点入栈,即分别将顶点V1和顶点V6入栈

第二步:弹出栈顶顶点V6并输出,遍历顶点V6的邻接顶点,即index == 3 和 index == 4 的顶点。将 index == 3 的顶点V4的入度减 1 ,发现不为0,则不入栈;将 index == 4 的顶点V5的入度减 1,发现不为0,则不入栈

第三步:弹出栈顶顶点V1并输出,然后遍历顶点V1的邻接顶点,即 index == 1,index == 2,index == 3的顶点。将 index == 1 的顶点V2的入度减 1等于1 ,不为0,则不入栈;将 index == 2的顶点V3的入度减 1等于0 ,则入栈;将 index == 3 的顶点V4的入度减 1等于0 ,则入栈

第四步:弹出栈顶顶点V4并输出,然后遍历顶点V4的邻接顶点,即 index == 4的顶点;将 index== 4 的顶点V5的入度减 1等于1 ,不为0,则不入栈

第五步:弹出栈顶顶点V3并输出,然后遍历顶点V3的邻接顶点,即 index == 1 和 index == 4 的顶点;将 index == 1 的顶点V2的入度减 1等于0 ,则入栈;将 index == 4 的顶点V5的入度减 1等于0 则入栈

第六步:弹出栈顶顶点V5并输出,顶点V5没有后继顶点

第七步:弹出栈顶顶点V2并输出,顶点V2没有后继顶点;

#include<stdio.h>
#include<stdlib.h>
#define INF 65535
//链栈
typedef struct stackNode{
int data;//存放入栈节点的下标
struct stackNode *next;
}snode,*stack;
//初始化栈
stack inits(){
stack s=(snode*)malloc(sizeof(snode));
s->next=NULL;
return s;
}
//入栈函数
stack ppush(stack s,int e){
snode* p=(snode*)malloc(sizeof(snode));
p->data=e;
p->next=s->next;
s->next=p;
return s;
}
//出栈-->栈顶数据返回
stack ppop(stack s,int *e)
{
if(s->next==NULL){
(*e)=-1;
return s;
}
snode* p=s->next;
(*e)=p->data;
s->next=p->next;
p->next=NULL;
free(p);
p=NULL;
return s;
}
//邻接表存有向图
//边单链表节点结构
typedef struct vNode{
char d;
struct edgeNode *first;
}Graph;
Graph g[105];
int n,m,ind[105];//入度
char topo[105];//保存拓朴序列
int find(char x){
for(int i=0;i<n;i++){
if(g[i].d==x){
return i;
}
}
}
int toposort(){
stack s=inits();
for(int i=0;i<n;i++){
if(ind[i]==0)
{
s=ppush(s,i);
}
}
int e;//出栈的点的下标
int k=0;//topo数组的下标
int flag=0;
for(int i=1;i<=n;i++){
s=ppop(s,&e);
if(e==-1){
printf("该图是带环图,无拓扑序列\n");
flag=1;
break;
}
topo[k]=g[e].d;
k++;
enode* p=g[e].first;
int j;
while(p!=NULL){
j=p->data;
ind[j]--;
if(ind[j]==0)
s=ppush(s,j);
p=p->next;
}
}
if(flag==0)
return 1;
else
return 0;
)
int main()
{
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++)
{
getchar();
scanf("%c",&g[i].d);
g[i].first=NULL;
}
char x,y;
int xi,yi;
for(int i=0;i<m;i++)
{
getchar();
scanf("%c %c",&x,&y);
xi=find(x);
yi=find(y);
//统计入度
ind[yi]++;
enode* p=(enode*)malloc(sizeof(enode));
p->data=yi;
p->next=g[xi].first;
g[xi].first=p;
}
int flag=toposort();
if(flag==1)
{
for(int i=0;i<n;i++)
{
printf("%c ",topo[i]);
}
}
printf("\n");
return 0;
} 三.关键路径
1.基本概念
1.1AOE网
AOE网即边表示活动的网,是与AOV网(顶点表示活动)相对应的一个概念。而拓扑排序恰恰就是在AOV网上进行的,这是拓扑排序与关键路径最直观的联系。AOE网是一个带权的有向无环图,其中顶点表示事件,弧表示活动,权表示活动持续的时间。下面的就是一个AOV网:
其中V1,V2,V3.......V9表示事件,a1.........a11表示活动,活动的取值表示完成该活动所需要的时间,如a1 = 6表示完成活动a1所需要的时间为6天。此外,每一事件Vi表示在它之前的活动已经完成,在它之后的活动可以开始,如V5表示活动a4和a5已经完成,活动a7和a8可以开始了
1.2AOE网的源点和汇点
由于一个工程中只有一个开始点和一个完成点,故将AOE网中入度为零的点称为源点,将出度为零的点称为汇点。
打个比方,我们现在有一个工程,就是将大象装进冰箱,那么源点就相当于我们现在接到这样一个任务,而汇点则表示我们完成了这个任务。那么我们之前所讲的打开冰箱门,将大象装进去,关上冰箱门就属于活动本身(即a1....a11所表示的信息),打开冰箱门所需要的时间就是活动所需要的时间,而完成某一个活动所到达的顶点就表示一个事件(冰箱门打开)。下图中的红色顶点V1表示源点, V9表示汇点。
1.3什么是关键路径
举个例子。
唐僧师徒从长安出发去西天取经,佛祖规定只有四人一起到达西天方能取得真经。假如师徒四人分别从长安出发,走不同的路去西天:孙悟空一个筋斗云十万八千里,一盏茶的功夫就到了;八戒和沙和尚稍慢点也就一天左右的时间;而唐僧最慢需要14年左右。徒弟到达后是要等着师傅的。那么用时最长的唐僧所走的路,就是取经任务中的关键路径。其他人走的路径属于非关键路径。由于AOE网中的有些活动是可以并线性进行的(如活动a1、a2和a3就是可以并行进行的),所以完成工程的最短时间是从源点到汇点的最长路径的长度。路径长度最长的路径就叫做关键路径。如下图中红色顶点和有向边构成的就是一条关键路径,关键路径的长度就是完成活动 a1、a4和a9、a10所需要的时间总和,即为 6+1+9+2 = 18

1.4ETV
ETV:事件最早发生时间,就是顶点的最早发生时间

事件V2的最早发生时间表示从源点V1出发到达顶点V2经过的路径上的权值之和,从源点V1出发到达顶点V2只经过了权值为6的边,则V2的最早发生时间为6,表示在活动a1完成之后,事件V2才可以开始;同理,事件V6要发生(即最早发生)需要活动a3和活动a6完成之后才可以,故事件V6的最早发生时间为 5 + 2 = 7。其他顶点(事件)的最早发生时间同理可的。需要说明,事件的最早发生时间一定是从源点到该顶点进行计算的。
1.5LTV
LTV:事件最晚发生时间,就是每个顶点对应的事件最晚需要开始的时间,如果超出此时间将会延误整个工期

前面在谈关键路径的概念时给出了一条上图中的关键路径,该关键路径( V1,V2,V5 ,V7,V9)的长度为18,为什么要提这个长度呢,因为要计算某一个事件的最晚发生时间,我们需要从汇点V9进行倒推。计算顶点V2的最晚发生时间为例,已知关键路径的长度为18,事件V2到汇点V9所需要的时间为 1 + 9 + 2 = 12,则事件V2的最晚发生时间为18-12 = 6,这时候我们发现,这和事件V2的最早发生时间不是一样吗?的确如此,对于关键路径上的顶点都满足最早发生时间 etv 等于 最晚发生时间 ltv 的情况,这也是我们识别关键活动的关键所在。再来计算一下事件V6的最晚发生时间,事件V6到汇点V9所需要的时间为 4 + 4 = 8,则事件V6的最晚发生时间为 18 - 8 = 10;相当于说活动a6完成之后,大可以休息3天,再去完成活动a9也不会影响整个工期
1.6ETE
ETE:活动的最早开工时间,就是弧的最早发生时间

活动a4要最早开工时间为事件V2的最早发生时间 6;同理,活动a9的最早开工时间为事件v6的最早发生时间 7。显然活动的最早开工时间就是活动发生前的事件的最早开始时间
1.7LTE
LTE:活动的最晚开工时间,就是不推迟工期的最晚开工时间

活动的最晚开工时间则是基于事件的最晚发生时间。比如活动a4的最晚开工时间为事件V5的最晚发生时间减去完成活动a4所需时间,即 7 - 1 = 6;活动 a9的最晚开工时间为事件V8的最晚发生时间减去完成活动a9所需时间,即 14 - 4 = 10;
从上面也就可以看出 只要知道了每一个事件(顶点)的ETV 和 LTV,就可以推断出对应的 ETE和 LTE . 此外还需要注意,关键路径是活动的集合,而不是事件的集合,所以当我们求得 ETV 和LTV 之后,还需要计算 ETE 和 LTE
2.关键路径算法
求关键路径的过程事实上最重要的就是上面提到的四个概念,ETV、LTV、ETE 和 LTE,求得了ETE与LTE之后只需要判断两者是否相等,如果相等则为关键路径中的一条边,则输出。为了清晰的明白算法的执行流程
首先求事件的最早发生事件ETV,这里使用的就是之前分享的拓扑排序,我们也走一遍,算是对拓扑排序的回顾。
第一步,建立图所对应的邻接表。

拓扑排序获得每一个事件的最早发生时间
初始时将ETV当中的数据都设置为0:

下面开始便是拓扑排序的过程了。
第二步:将入度为零的顶点V1入栈;

第三步:顶点V1出栈,并遍历顶点V1的邻接顶点 ,即 index 分别为 1,2,3 的顶点V2、 V3和顶点V4 ,并将邻接顶点的入度减1,判断是否为 0 ,如果为 0 则入栈。首先遍历 index = 1 顶点V2 ,并将顶点V2的入度减 1 ,发现为零,则将顶点V2入栈, 判断 ETV[0] + w(V1,V2) 是否大ETV[1] , 发现大于,则将 ETV[1] 更新为 ETV[0] + w(V1,V2) = 6;同理遍历 index = 2 的顶点 V3 ,将顶点V3入栈,并将ETV[2] 更新为 4 ;遍历 index = 3 的顶点 V4 ,将顶点 V4入栈,并将 ETV[3] 更新为 5

第四步:弹出栈顶元素V4并遍历顶点V4的邻接顶点V6 . 将顶点V6的入度减一,并将 ETV[5] 更新为 ETV[3] + w(V4,V6),即为7.

第五步:弹出栈顶元素 V6 并遍历邻接顶点V8

第六步:弹出栈顶元素 V3,并遍历V3 的邻接顶点V5

第七步:弹出栈顶元素V2,并遍历V2的邻接顶点V5

第八步:弹出栈顶元素V5 ,并遍历V5的邻接顶点V7和V8

第九步:弹出栈顶元素 V8,并遍历V8的邻接顶点V9

第十步:弹出栈顶元素V7 ,并遍历V7的邻接顶点V9

第十一步:将栈顶元素V9出栈

其中,我们将拓扑排序过程中的出栈序列依次入栈,即拓扑排序结束时,我们响应的保存了一个
出栈序列V1 V4 V6 V3 V2 V5 V8 V7 V9,用于逆向计算事件的最晚发生时间:

根据事件的最早发生时间ETV推断事件的最晚发生时间 LTV
通过拓扑排序我们获得了每一个顶点的最早发生时间 ETV,紧接着便可以计算 LTV了。
计算LTV的值,即每一个顶点的最晚发生时间值,初始时将LTV的值初始化为汇点V9的时间 18

紧接着则是访问之前的出栈序列栈 。
首先将顶点V9出栈,什么都不做

第二步:将顶点V7出栈,并判断LTV[6] 与 LTV[8] - w(V7,V9)的大小,将 LTV 更新为 LTV[8] -w(V7,V9) =16

第三步:将顶点V8出栈,更新 LTV[7] 为 LTV[8] - w(V8,V9)= 14

第四步:将顶点V5 出栈,并遍历V5的邻接顶点V7和V8。用邻接顶点V7的LTV值减去活动a7值,并与顶点V5的LTV值进行比较,将LTV[4] 更新为 7;同理用邻接顶点V8的LTV值减去活动a8的值,并与V5顶点的值进行比较,发现相等不做更新

第五步,弹出栈顶元素V2 ,并遍历 V2的邻接顶点V5 , 用顶点V5的LTV(最晚发生时间) 减去活动a4所需时间,即为6,将顶点V2的LTV[1] 更新为6

第六步,弹出栈顶事件(顶点)V3 ,并更新顶点V3的最晚发生时间

第七步:弹出栈顶事件V6(顶点)

第八步:弹出栈顶元素V4并更新其最晚发生时间

第九步:弹出栈顶元素V1并更新其最晚发生时间。使用事件V2的最晚发生时间 6 减去活动a1所需时间6等于0,与顶点V1的最晚时间相比较并更新为0。需要说明,事实上源点的最晚发生时间与最早发生时间都为0,毋庸置疑

此时我们得到每个事件(顶点)的最早发生时间和最晚发生时间,但关键路径是活动的集合,所以接下来我们用事件的最早发生时间和最晚发生时间计算出活动(弧)的最早与最晚发生时间即可

计算活动的最早与最晚开工时间
第一步:从源点V1开始,遍历源点的邻接顶点 V2, 将弧 <V1,V2> 上的活动a1 的最早发生时间更新为源点 V1的最早发生时间 0,将活动a1 的最晚发生时间更新为事件V2的最晚发生时间 6 减去活动 a1所需要的时间6,即为0. 判断活动a1的最早发生时间与最晚发生时间是否相等,如果相等则为关键活动,并输出。同理遍历源点v1的邻接顶点v3和v4,并更新弧a2和a3的最晚开工时间与最早开工时间

第二步:访问顶点 V2,遍历V2的邻接顶点V5 . 将活动a4的最早发生时间更新为事件 V2的最早发
生时间,将活动 a4的最晚发生时间更新为事件 V5的最晚发生时间 7 减去活动 a4 所需时间 1,即为6

第三步:访问顶点V3,遍历V3的邻接顶点V5 . 将活动a5的最早发生时间更新为事件V3的最早发生时间 4 ,将活动a5的最晚发生时间更新为事件V5的最晚发生时间 7 减去活动a5所需时间 1,即为6.

第四步:访问顶点V4,遍历该顶点的邻接顶点V6, 将活动a6的最早发生时间更新为事件V4的最
早发生时间5,活动a6的最晚发生时间为事件V6的最晚发生时间10 减去 活动 a6 所需要的时间 2,即为8.

第五步:访问顶点 V5,并分别遍历该顶点的邻接顶点V7 和顶点 V8。将活动a7和a8的最早发生时
间更新为时间V5的最早发生时间7,最晚发生时间也更新为7

第六步:访问顶点V6,并遍历该顶点的邻接顶点 V8,将活动a9的最早发生时间更新为事件V6 的
最早发生时间7,最晚发生时间更新为事件V8的最晚发生时间 14 减去活动a9所需时间4 ,即为10.

第七步:访问顶点 V7,更新活动 a10的最早发生时间和最晚发生时间

第八步:访问顶点V8 ,更新活动 a11的最早发生时间和最晚发生时间

第九步:访问顶点V9 ,没有邻接顶点,什么都不做

#include<stdio.h>
#include<stdlib.h>
#define INF 65535
//链栈
typedef struct stackNode{
int data;//存放入栈节点的下标
struct stackNode *next;
}snode,*stack;
//初始化
stack inits(){
stack s=(snode*)malloc(sizeof(snode));
s->next=NULL;
return s;
}
//入栈函数:
stack ppush(stack s,int e)
{
snode* p=(snode*)malloc(sizeof(snode));
p->data=e;
p->next=s->next;
s->next=p;
return s;
}
//出栈-->栈顶数据返回
stack ppop(stack s,int *e)
{
if(s->next==NULL)
{
(*e)=-1;
return s;
}
snode* p=s->next;
(*e)=p->data;
s->next=p->next;
p->next=NULL;
free(p);
p=NULL;
return s;
}
//------------------------
//邻接表存带权有向图-----> AOE网
//边单链表节点结构
typedef struct edgeNode
{
int data;//存放入栈节点的下标
struct edgeNode *next;
int w;//1.边权
}enode;
//顶点数组
typedef struct vNode
{
char d;
struct edgeNode *first;
}Graph;
Graph g[105];
int n,m;
int ind[105];//入度
int etv[105];//事件的最早发生时间
int ltv[105];//事件的最晚发生时间
//char topo[105];//保存拓扑序列
int topo[105];//保存拓扑序列----基于顶点下标
int find(char x)
{
for(int i=0;i<n;i++)
{
if(g[i].d==x)
{
return i;
}
}
}
void toposort()
{
stack s=inits();//初始化栈
for(int i=0;i<n;i++)
{//初始化etv数组
etv[i]=0;
}
for(int i=0;i<n;i++)
{
if(ind[i]==0)
{
s=ppush(s,i);
}
}
int e;//出栈的点的下标
int k=0;//topo数组的下标;
int flag=0;
for(int i=1;i<=n;i++)
{
s=ppop(s,&e);
topo[k]=e;//出栈的顶点的下标 保存在topo序列里面
k++;
enode* p=g[e].first;
int j;
while(p!=NULL)
{
j=p->data;//j就是e的出边邻接点 e---->j
if(etv[j]<(etv[e]+p->w))
{//求etv
etv[j]=etv[e]+p->w;
}
ind[j]--;
if(ind[j]==0)
{
s=ppush(s,j);
}
p=p->next;
}
}
}
void CriticalPath()
{
int end=topo[n-1];//0 ~~ n-1
for(int i=0;i<n;i++)
{
//初始化ltv,将每个点的最晚发生时间都初始化成终点的最早发生时间即可
ltv[i]=etv[end];
}
int x;
//逆拓扑序 更新ltv
for(int i=n-2;i>=0;i--)
{
x=topo[i];//x点的最晚发生时间
enode* p=g[x].first;
while(p!=NULL)
{
int j=p->data;//x-->j
if(ltv[x]>(ltv[j]-p->w))
{
ltv[x]=ltv[j]-p->w;
}
p=p->next;
}
}
printf("以下是关键活动:\n");
//遍历所有的边,求每个边的ete lte
int ete,lte;
for(int i=0;i<n;i++)
{
for(enode* p=g[i].first;p!=NULL;p=p->next)
{
int j=p->data;///i--->j
ete=etv[i];
lte=ltv[j]-p->w;
if(ete==lte)
{
printf("%c %c\n",g[i].d,g[j].d);
}
}
}
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++)
{
getchar();
scanf("%c",&g[i].d);
g[i].first=NULL;
}
char x,y;
int xi,yi,wi;
for(int i=0;i<m;i++)
{
getchar();
scanf("%c %c %d",&x,&y,&wi);
xi=find(x);
yi=find(y);
//统计入度
ind[yi]++;
enode* p=(enode*)malloc(sizeof(enode));
p->data=yi;
p->w=wi;//
p->next=g[xi].first;
g[xi].first=p;
}
toposort();
CriticalPath();
return 0;
} 总结
toposort为关键路径服务,关键路径代码较难需要一些时间消化!

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容





所有评论(0)