1、前言

高斯过程，是随机过程的一种。高斯过程回归，和线性回归有些相似，总之就是用数据去拟合出一条线，然后做预测。
数学基础：【概率论与数理统计知识复习-哔哩哔哩】

2、引入

在了解高斯过程之前。我们得知道什么是高斯分布。高斯分布，在一维的时候，给定期望和方差，可以唯一确定一个概率分布。在期望为0，方差为1高斯分布，其密度函数为

这是一维的情况，同理的还有多维高斯分布。所谓多维高斯分布，其实就是将原本一维的高斯分布在不同方位堆叠，如果维度之间存在关系，则会就不能简单堆叠。假如我们有p维的高斯分布，那么相应的就要给出p维的期望，而对应的方差就变成了$p\times p$维协方差矩阵$\boxed{刻画不同维度之间的关系}$。

那如果说我们的维度扩展到了无限维呢？当维度扩展到无限维，我们则称为高斯过程。相应的，既然是无限维，$\boxed{那么理应我们就该用一个无限维的期望和协方差矩阵去表达}$。但是无限维怎么表达出来？没错！就是用函数。我们就要让期望遵循一个函数，协方差矩阵也同样遵循一个函数即可。

3、高斯过程

不严谨的来说，实际上就是定义在连续域上的随机变量的集合，这个连续域一般是空间或者时间。并且对任意一个（或多个）时间或者空间，其仍然服从高斯分布。其可表示为
$$f(x)\sim GP(m,K)$$

$\boxed{即f(x)是服从高斯过程，其中m为均值函数，K为协方差函数}$

4、高斯过程回归

首先什么是线性回归，所谓线性回归，就是用一条直线去拟合现有的数据，然后进行预测，即

但是说，假如我们的数据它的轨迹就不是线性的，而是这样呢？

一般情况下，面对这种问题，一种思路就是进行数据升维。一般情况下，我们认为高维空间比低维空间更加容易线性可分。

比如，我们有一个点$x$，其有两个维度，将其表示成向量，则
$$x={\left(\begin{array}{cc}{x}^1& x^2\end{array}\right)}^T$$
生成三维，第三个维度我们作
$$x={\left(\begin{array}{ccc}{x}^1& x^2& (x^1-x^2{)}^2\end{array}\right)}^T$$
再来回顾一下我们的线性回归的直线方程
$$f(x)=w^{T}x$$
如果对数据x进行升维操作，升维之后的数据我们用$\varphi (x)$表示，那么就得到
$$f(x)=w^T\varphi (x)$$
并且，我们可以认为此时$f(x)$就是一个服从高斯过程的函数，可以理解成每一个点的x轴就是对应高斯过程中的某个时间或者空间。
$$f(x)\sim GP(m,K)$$
这里的$m$就是$f(x)$的期望函数，而$K$就是协方差函数。

$\boxed{\mathbf{其实也就是对于任意一个点}\mathbf{x}，它都有自己的一个属于期望和方差，也就是每个点都服从自己的一个高斯分布}$。那么将所有的数据点联合起来，所有点的期望堆叠起来，就成了期望函数，所有点的方差（或协方差矩阵）堆叠起来，加上数据点之间是否存在关系，就成了协方差矩阵。

5、求解

我们先定义一些量
$$\begin{gathered} X={\left(\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right)}_{n\times p}^T \\ Y={\left(\begin{array}{cccc}{y}_1& y_2& \cdots & y_n\end{array}\right)}_{n\times 1}^T \end{gathered}$$
我们知道，要去做预测每一个点对应的y值，都是要经过
$$\begin{gathered} f(x_i)=w^T{x}_i \\ {y}_i=f(x_i)+ϵ \end{gathered}$$
其中$ϵ\sim N(0,{\sigma }^2)$的过程噪声。也就是，对于每一个样本的，他都是要先计算直线方程，然后再加上一个过程噪声。

在传统的贝叶斯线性回归中，我们认为权重$w$是随机变量，即我们就是要先求出后验$P(w|X,Y)$。

然后再计算出$f(x)$，再到$y$。即
$$P(y^{\ast }|X,Y,x^{\ast })={\int }_{w}P(y^{\ast }|w,X,Y,x^{\ast })P(w|X,Y,x^{\ast })dw={\int }_{w}P(y^{\ast }|w,x^{\ast })P(w|X,Y)dw$$
$y^{\ast },x^{\ast }$为我们要预测的点。具体可以看【机器学习】贝叶斯线性回归

在高斯过程回归中，从函数的角度去理解的话，实际上我们就不管那个后验w了，而是从函数$f(x)$出发。

什么意思呢？比如，现在我们作预测，预测值标记为$y^{\ast },x^{\ast }$。

那么就会有
$$\begin{gathered} f(x^{\ast })=w^T{x}^{\ast } \\ {y}^{\ast }=f(x^{\ast })+ϵ \end{gathered}$$
按照正常的思路，对这个预测问题，里面的权重w必然是后验，我们可以任意取设定。

$\boxed{\mathbf{但是在如果是从}\mathbf{f}(\mathbf{x})的角度去看的话，却不是这样，里面的\mathbf{w}\mathbf{是先验}}$

对于我们的训练数据集也是如此
$$\begin{gathered} f(x)=w^{T}x \\ y=f(x)+ϵ\text{\hspace{1em}(1.1)} \end{gathered}$$
最终我们要求出的是$y^{\ast }$，所以我们可以这样
$$P(y^{\ast }|X,Y,x^{\ast })=P(y^{\ast }|y,x^{\ast })\text{\hspace{1em}(1.2)}$$
其中$y$来自式(1.1)，根据式(1.1)，$y$已经充分代表了$X,Y$这些数据点，故可直接用$y$去代表。

或者我们不妨去假设的通俗一些，将式(1.1)中$y$当作是先验（因为它的w）是先验。而$y^{\ast }|y,x^{\ast }$自然就是由先验到了后验的过程。

如果还是有点迷糊，看一下接下来的流程估计就懂了。

6、流程

首先，要先求出先验$f(X)$。不是$f(x)$吗？怎么变成这玩意儿了？呃，主要前面符号没对齐，懒得改了。我们前面说过，高斯过程回归是要我们所有的点联合组成的期望和协方差函数。而我们前面用$X$表示了数据集的横坐标，那自然就是要求的是$f(X)$，所以请不要感到疑惑（$f(X)$代表全部的训练数据）

我们之前说过，要对x升维，$\boxed{\mathbf{假设从}\mathbf{p}\mathbf{维升成}\mathbf{q}\mathbf{维}}$，得到的结果我们同样表示为
$$\Phi ={\left(\begin{array}{cccc}\varphi (x_1)& \varphi (x_1)& \cdots & \varphi (x_n)\end{array}\right)}_{n\times q}^T$$
所以由
$$f(X)=w^T\Phi ={\Phi }^{T}w$$
我们前面说过，此时的w是先验，是我们任意假设的，我们假设它$w\sim N(0,\Sigma )$（这里好多人都对这个有问题，我个人认为这个初始化成期望为0，纯粹就是为了简单，并且在很多情况下，我们都会对数据进行均值化，所以设成0。但都说它是先验了，既然是先验，如果我们有先验知识，知道它可能期望为1，那么我们就设为1。如果我们不知道它的期望为多少，就设为0。后面加入数据之后，自然会修正先验的值，但这并不是说先验对结果就没有影响，有是一定有的，但是远远没有我们想的那么重要（预测点距离训练集越近，则先验越不重要。反之则更重要）。

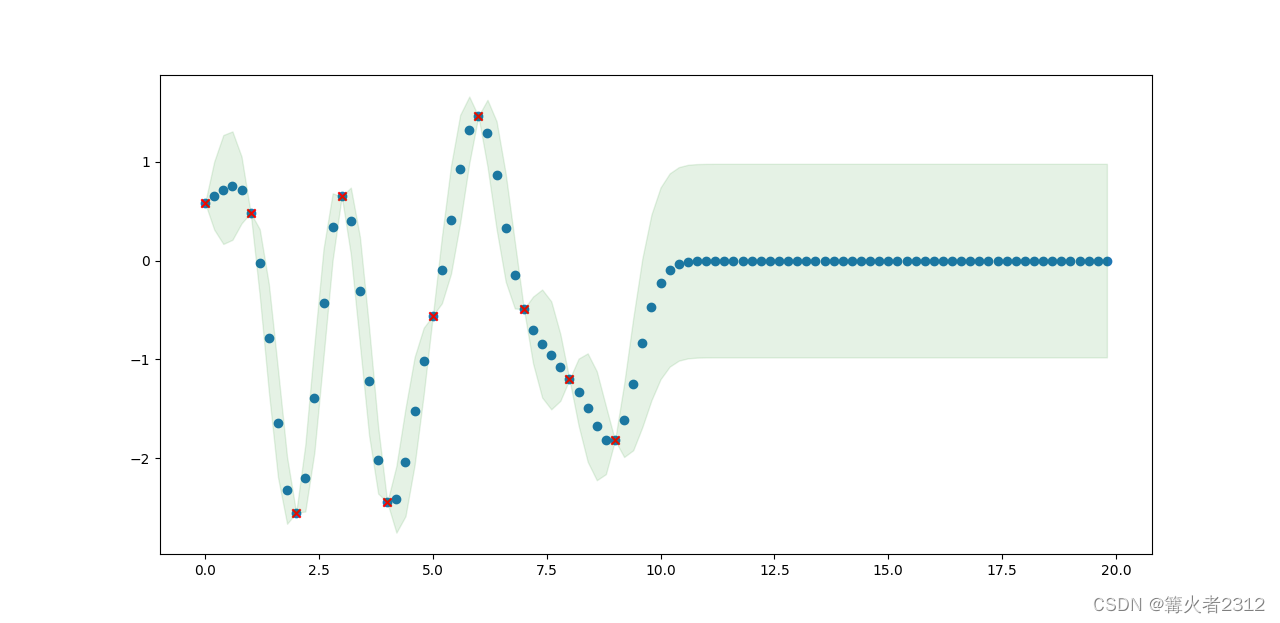
如果你还是不理解这句话，我们可以看看下面的例子（先验均值设为0）

在上面，红色的点是我们的训练集，绿色的点是预测值。阴影部分是每个预测点的置信区间。可以看到，我们的训练集是从0到10，预测值是0到20。在0到10，预测值很正常，置信区间也很小。但超过10以后，预测值就趋近于0。然后置信区间很大。

我们再来看先验均值为1的

​ 看到没有，远离训练集的测试集（10到20）那部分，此时的均值都是为1。

​ 言归正传，我们说过要将$f(X)$当作是一个高斯过程。那就是要求出它的期望函数和协方差函数。我们不妨设为${\mu }_p,{\Sigma }_p$
$${\mu }_k=\mathbb{E}[f(X)]=\mathbb{E}[{\Phi }^{T}w]={\Phi }^T\mathbb{E}(w)={\Phi }^T\ast 0=0$$

$$\begin{array}{c}\begin{array}{rl}{\Sigma }_k=& \mathbb{E}\left[(f(X)-{\mu }_k)(f(X)-{\mu }_k{)}^T\right]\\ =& \mathbb{E}\left[f(X)f(X{)}^T\right]\\ =& \mathbb{E}\left[{\Phi }^{T}w{w}^T\Phi \right]\\ =& {\Phi }^T\mathbb{E}\left[w{w}^T\right]\Phi \\ =& {\Phi }^T\Sigma \Phi \end{array}\end{array}\text{\hspace{1em}(2.1)}$$

6.1、核函数

我们仔细看里面的$\Phi$，这个东西是数据x进行高维映射之后得到的。我们上面提到的是从二维上升到了三维。但假如在实践中，我们要将其升维到的维度很高，难道我们每一次都要去计算出升维后的对应的$\varphi (x)$吗？这无疑会大大增加我们的计算量。

那有没有一种方法，能够不计算出$\varphi (x)$，又能够计算出${\Phi }^T\Sigma \Phi$？

一般情况下，我们就是利用核函数，即当有两个点时，令$k(x_1,x_2)=<\varphi (x_1),\varphi (x_2)>$，$<>$表示内积。所以对于${\Phi }^T\Sigma \Phi$，我们令$k(x_1,x_2)=<{\Sigma }^{\frac{1}{2}}\varphi (x_1),{\Sigma }^{\frac{1}{2}}\varphi (x_2)>$。

最后，我们对所有的点都进行转化，此时我们用大写的$K(X,X)$表示，所以
$${\Sigma }_k=K(X,X)$$
在这里就仅仅作一点简单的介绍了，具体有哪些核函数，怎么推导的，在这里不作介绍，感兴趣的可自行百度。

得到了高斯过程$f(x)$的参数。那么对于$Y\sim N(0,K(X,X)+{\sigma }^2\mathbb{I})$。$\mathbb{I}$为单位矩阵。这个不懂的可以看线性动态系统中的概率求解

6.2、问题

所以，假设我们要求解的是$Y^{\ast }=\left(\begin{array}{cccc}{y}_1^{\ast }& y_2^{\ast }& \cdots & y_n^{\ast }\end{array}\right)$。为了避免混乱，我们不妨先求出$f(X^{\ast })=\left(\begin{array}{cccc}{x}_1^{\ast }& x_2^{\ast }& \cdots & x_n^{\ast }\end{array}\right)$

那么如何求出$P(f(X^{\ast })|Y,X^{\ast })$呢？

6.3、定理

给定
$$x,y\sim N\left(\begin{array}{c}\left(\begin{array}{c}{\mu }_x\\ {\mu }_y\end{array}\right),\left(\begin{array}{cc}{\Sigma }_{xx}& {\Sigma }_{xy}\\ {\Sigma }_{yx}& {\Sigma }_{yy}\end{array}\right)\end{array}\right)\text{\hspace{1em}(2.2)}$$
则
$$P(x|y)\sim N(x|{\mu }_k+{\Sigma }_{xy}{\Sigma }_{yy}^{-1}y,{\Sigma }_k)$$

其中${\mu }_k={\mu }_x-{\Sigma }_{xy}{\Sigma }_{yy}^{-1}{\mu }_y$，${\Sigma }_k={\Sigma }_{xx}-{\Sigma }_{xy}{\Sigma }_{yy}^{-1}{\Sigma }_{yx}$。对推导过程感兴趣的可以看一下线性动态系统中的概率求解

为什么要引入这个东西呢？我们如果我们将$f(X^{\ast }),Y$当作是上面式(2.1)中的x，y呢？这不就行了吗？
$$f(X^{\ast }),Y\sim N\left(\begin{array}{c}\left(\begin{array}{c}{\mu }_f\\ {\mu }_Y\end{array}\right),\left(\begin{array}{cc}{\Sigma }_{ff}& {\Sigma }_{fY}\\ {\Sigma }_{Yf}& {\Sigma }_{YY}\end{array}\right)\end{array}\right)$$

将协方差矩阵转化成核函数，自然得到（${\Sigma }_{Yf}$推导过程和式(2.1)一致，此处不作推导）。
$$f(X^{\ast }),Y\sim N\left(\begin{array}{c}\left(\begin{array}{c}{\mu }_f\\ {\mu }_Y\end{array}\right),\left(\begin{array}{cc}K(X^{\ast },X^{\ast })& K(X^{\ast },X)\\ K(X,X^{\ast })& K(X,X)+{\sigma }^2\mathbb{I}\end{array}\right)\end{array}\right)$$
我们要求的曾在式(1.2)中提到，转化成比较宽泛的表达就是
$$P(f(X^{\ast })|Y,X^{\ast })=P(f(X^{\ast })|Y)$$
原因是$f(X^{\ast })$中，根据式(1.1)可知其已经包含了$X^{\ast }$，所以后面条件中的$X^{\ast }$可有可无。

所以我们就是要求$P(f(X^{\ast })|Y)$。我们直接套公式就可以了，设其期望为${\mu }_r$，协方差矩阵为${\Sigma }_r$。

所以
$$\begin{gathered} {\mu }_r={\mu }_f-K(X^{\ast },X){\left[K(X,X)+{\sigma }^2\mathbb{I}\right]}^{-1}{\mu }_Y+K(X^{\ast },X){\left[K(X,X)+{\sigma }^2\mathbb{I}\right]}^{-1}Y; \\ {\Sigma }_r=K(X^{\ast },X^{\ast })-K(X^{\ast },X){\left[K(X,X)+{\sigma }^2\mathbb{I}\right]}^{-1}K(X,X^{\ast }); \end{gathered}$$
得到$f(X^{\ast })$的参数，那么由式(1.1)，再简单整理一下，自然可得$Y^{\ast }|f(X^{\ast })$
$$\begin{gathered} Y^{\ast }|f(X^{\ast })\sim N({\mu }_f+K(X^{\ast },X){\left[K(X,X)+{\sigma }^2\mathbb{I}\right]}^{-1}(Y-{\mu }_Y), \\ K(X^{\ast },X^{\ast })-K(X^{\ast },X){\left[K(X,X)+{\sigma }^2\mathbb{I}\right]}^{-1}K(X,X^{\ast })+{\sigma }^2\mathbb{I}) \end{gathered}$$

7、结束

以上，便是高斯过程回归的全部内容了，推导过程并不严谨。如有问题，还望指出，阿里嘎多。