A*算法可采纳性、一致性、最优性证明

前言：

【网络上A*算法相关的文章都集中算法的步骤及代码上，对算法原理介绍不多，因此特意花了几天时间阅读原论文，对其中的定理、引理、推论进行说明，希望能够知其然并知其所以然。由于本人水平有限，关于A*算法最优性的证明部分一知半解，也希望本文能抛砖引玉，望多多交流、答疑解惑。】

以下内容均基于A*算法的原论文：A Formal Basis for the Heuristic Determination of Minimum Cost Paths

论文链接：https://ieeexplore.ieee.org/abstract/document/4082128/references#references

一、相关概念

1.1、评估函数$\hat{f}$

Evaluation Function作用：用于从多个可选节点中选出路径拓展（expand）的下一个节点

• 例如开始节点$S$，当前节点为$n$，需要从$n$的相邻可选节点（successor）中选择一个节点进行路径拓展，好的评估函数能在节点拓展后尽可能靠近目标节点；
• 论文中以可选节点评估函数值最小的节点作为要拓展的节点

1.2、算法步骤

步骤1：将开始节点$S$的状态记为open（文中为mark as open），计算$\hat{f}(S)$；

步骤2：从所有状态为open的节点中选择评估函数值最小的节点作为要拓展的节点（节点$n$）；

步骤3：若$n$为目标节点，则算法结束，否则，执行步骤4；

步骤4：将$n$记为closed，对$n$的所有相邻节点计算评估函数值，对于某个相邻节点$n_i$，评估函数值原值与现值分别计为${\hat{f}}_{n_i}^{Before}$、${\hat{f}}_{n_i}^{After}$

• 若不是closed，则将该节点记为open；
• 若是closed，则需要比较${\hat{f}}_{n_i}^{Before}$、${\hat{f}}_{n_i}^{After}$​
  • 若${\hat{f}}_{n_i}^{Before}\le {\hat{f}}_{n_i}^{After}$​，则保持不变，仍为closed；
  • 若${\hat{f}}_{n_i}^{After}<{\hat{f}}_{n_i}^{Before}$，则将节点$n_i$​从的状态由closed调整为open（文中为remark as open）；
• 继续执行步骤2

说明：编程实现时，可以使用集合open set、closed set，节点在两个集合中的移动（添加、删除）就是节点状态的转换（open <—> closed）；

1.3、评估函数的设计思路

场景：开始节点$S$到目标节点$E$之间存在一条经过节点$n$的最短路（an optimal path），记该路径的实际成本为$f(n)$，则$f(S)=f(n)=h(S)$，都表示该路径的实际成本，其中$h(S)$的含义之后会解释。

基于最短路的定义有一个朴素的结论（顾名思义）：

• 若节点$n$在最短路上，则$f(n)=f(s)$；
• 若节点$n$不在最短路上，则$f(n)>f(S)$

该结论说明$f(n)$可以用于选择下一步要拓展的节点，因为$f(n)$不是先验已知的，可以使用评估函数$\hat{f}(n)$估计$f(n)$​

详见原文：

$f(n)$可以拆分为两部分：
$$\begin{gathered} f(n)=g(n)+h(n) \\ 其中，g(n)为最优路径上开始节点S到节点n的实际成本； \\ h(n)为最优路径上节点n到目标节点E的实际成本 \end{gathered}$$
同样的，$\hat{f}(n)=\hat{g}(n)+\hat{h}(n)$

• $\hat{g}(n)$是对$g(n)$的估计，表示截至目前开始节点$S$到节点$n$的成本（the smallest cost so far），该值动态更新，但始终满足$\hat{g}(n)\ge g(n)$​，即“局部最小值”不小于“全局最小值”；
• $\hat{h}(n)$是对$h(n)$的估计，表示节点$n$目标节点$E$的成本估计值（下一章节会证明$\hat{h}(n)$满足一定条件时，算法一定能找到最优解）；

二、可采纳性

2.1、可采纳性说明

定理1：若对于所有节点$n$，均满足$\hat{h}(n)\le h(n)$​，则A*算法满足可采纳性（A* is admissible），即算法能找到起点与目标节点之间的最短路

We call an algorithm admissible if it is guaranteed to find an optimal path from S to a preferred goal node of S for any graph.

证明该定理需要使用一些前置结论：

引理1：对于任意非关闭状态（nonclosed）的节点$n$以及从$S$到$n$的任意最短路$P$，在$P$上都存在一个状态为开（open）的节点$n^{\prime }$满足$\hat{g}(n^{\prime })=g(n^{\prime })$

推论：假定对于所有节点$n$，均满足$\hat{h}(n)\le h(n)$并且A*算法未结束，则对于从$S$到目标节点的任意最短路$P$，在$P$上都存在状态为开（open）的节点$n^{\prime }$满足$\hat{f}(n^{\prime })\le f(S)$

2.2、前置结论证明

2.2.1、引理1证明

引理1：对于任意非关闭状态（nonclosed）的节点$n$以及从$S$到$n$的任意最短路$P$，在$P$上都存在一个状态为开（open）的节点$n^{\prime }$满足$\hat{g}(n^{\prime })=g(n^{\prime })$

证明思路：通过证明$\hat{g}(n^{\prime })\ge g(n^{\prime })$ 且 $\hat{g}(n^{\prime })\le g(n^{\prime })$，可得$\hat{g}(n^{\prime })=g(n^{\prime })$

（1）对于$\hat{g}(n^{\prime })\ge g(n^{\prime })$

其中，易知$\hat{g}(n^{\prime })\ge g(n^{\prime })$（可见章节1.3中关于$\hat{g}(n)$的说明），因此仅需证明$\hat{g}(n^{\prime })\le g(n^{\prime })$

（2）对于$\hat{g}(n^{\prime })\le g(n^{\prime })$

证明：

设$P=(S=n_0,n_1,n_2,...,n_k=n)$

A*算法开始执行时：

• 节点$S$为open（可认为$n^{\prime }=S$），此时$\hat{g}(S)=g(S)=0$，引理成立；

A*算法执行时的某一状态：

• 设$\Delta$为$P$ 上所有状态为closed的节点$n_i$的集合，集合内节点均满足$\hat{g}(n_i)=g(n_i)$，$\Delta$非空（因为$S$一定在其中），设最后一个进入集合$\Delta$的节点为$n^{\ast }$（with the highest index），易知$n^{\ast }\ne n$（因为$n$​为nonclosed），设$n^{\prime }$为路径$P$上$n^{\ast }$的“子节点”（successor），$n^{\prime }$可能为节点$n$，节点$n^{\ast }、n^{\prime }$之间的成本为$c_{n^{\ast },n^{\prime }}$​
• 则$\hat{g}(n^{\prime })\le \hat{g}(n^{\ast })+c_{n^{\ast },n^{\prime }}$
  • 因为$\hat{g}(n)$的更新方式为：$\hat{g}(n^{\prime })=min(\hat{g}(n^{\prime }),\hat{g}(n^{\ast })+c_{n^{\ast },n^{\prime }})$​，可证明该不等式成立
• 则$\hat{g}(n^{\ast })=g(n^{\ast })$，因为$n^{\ast }\in \Delta$
• 则$g(n^{\prime })=g(n^{\ast })+c_{n^{\ast },n^{\prime }}$，因为$n^{\prime }$在$P$上
• 考虑以上三个结论可以推导出$\hat{g}(n^{\prime })\le \hat{g}(n^{\ast })+c_{n^{\ast },n^{\prime }}=g(n^{\ast })+c_{n^{\ast },n^{\prime }}=g(n^{\prime })$​

根据上述分析，证明得到$\hat{g}(n^{\prime })=g(n^{\prime })$，论文中描述如下：

2.2.2、推论证明

推论：假定对于所有节点$n$，均满足$\hat{h}(n)\le h(n)$并且A*算法未结束，则对于从$S$到目标节点的任意最短路$P$，在$P$上都存在状态为开（open）的节点$n^{\prime }$满足$\hat{f}(n^{\prime })\le f(S)$

基于引理1，可知存在一个节点$n^{\prime }$，其$\hat{g}(n^{\prime })=g(n^{\prime })$

对于该节点（该节点在最短路上，因此$f(n^{\prime })=f(S)$）：

$\hat{f}(n^{\prime })=\hat{g}(n^{\prime })+\hat{h}(n^{\prime })=g(n^{\prime })+\hat{h}(n^{\prime })\le g(n^{\prime })+h(n^{\prime })=f(n^{\prime })=f(S)$

结论成立

2.3、定理证明

定理1：若对于所有节点$n$，均满足$\hat{h}(n)\le h(n)$​，则A*算法满足可采纳性（A* is admissible）

所有节点均满足$\hat{h}(n)\le h(n)$，若能证明A*算法不能找到从$S$到目标节点的最短路而结束，则说明定理1不成立，否则定理1成立

可分为3种情况分别讨论：

• case1：算法在非目标节点结束；
• case2：算法不能正常结束（可理解为“死循环”）；
• case3：算法在目标节点结束，但是所得路径不是最短路。

2.3.1、case1分析

根据章节1.2中所述A*算法步骤，算法仅在目标节点处终止，因此case1所述情况不存在。

2.3.2、case2分析

设节点$S$到目标节点$t$的最短路成本为$f(S)$，路段长度至少为$\delta$，记$M=f(S)/\delta$

根据$M$值，分两种情况讨论是否算法不能正常结束的可能性

（1）对于$M$步之后

则对于$M$步之后的节点$n$，一定有$\hat{f}(n)\ge \hat{g}(n)\ge g(n)>M\delta =f(S)$

根据推论1，A*算法结束之前，存在一个节点$n^{\prime }$，使得$\hat{f}(n^{\prime })\le f(S)$​

因此，$\hat{f}(n^{\prime })<\hat{f}(n)$，说明$M$步之后拓展的节点一定会在最短路上，因此会在目标节点处结束

（2）对于$M$​步之前

设$X(M)$为$M$步之前（包含$M$）从节点$S$可到达的（accessible）节点集合，$v(M)$为$X(M)$​中的节点数

则对于$X(M)$中的任意节点$n$，其状态由close重新调整为open最多为有限次（can be reopen at most a finite number of times）记为$\tilde{p}(n,M)$，因为从节点$S$到节点$n$（不超过$M$​步）的路径数有限

令：$p(M)=\underset{n\in X(M)}{\max }\tilde{p}(n,M)$，表示集合$X(M)$中各节点可能被reopen的最大次数

因此，在至多$v(M)p(M)$次循环（ 节点拓展Expansion，对应算法步骤2、3、4）之后（循环过程中已拓展的路径上的路段数一定不超过$M$），所有节点都会永久closed，因此算法会结束

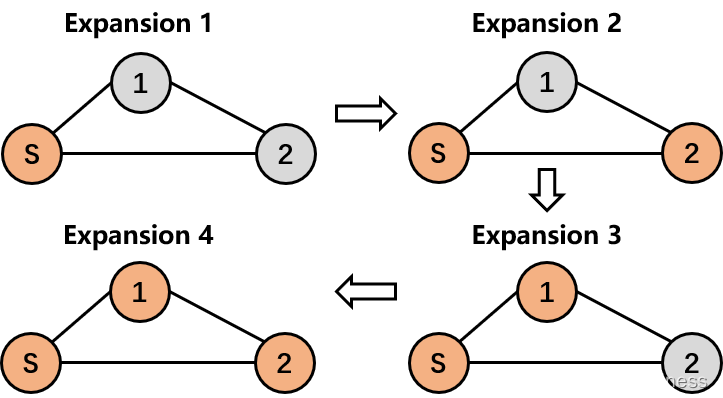
以上图为例进行说明（其为$M$步可到达的所有节点构成的子图）：

• 第一次拓展，记开始节点$S$为closed，计算节点1、2的评估函数值；
• 第二次拓展，选择节点2（假设节点2评估函数值更小，记其为closed），开始节点不会被reopen（因为其始终不满足算法步骤4中的节点reopen的条件）；
• 第三次拓展，选择节点1（记其为closed），假设节点2被reopen；
• 第四次拓展，选择节点2（记其为closed），假设节点1不被reopen，则此时所有节点均为closed，算法结束。

根据上述分析，可知算法一定会正常结束（到达目标节点）

2.3.3、case3分析

对于目标节点$t$，若算法找到一条非最短路，则$\hat{f}(t)>f(S)$

根据推论1，A*算法结束之前，存在一个节点$n^{\prime }$，使得$\hat{f}(n^{\prime })\le f(S)$

可得$\hat{f}(n^{\prime })\le \hat{f}(t)$，因此，在步骤2时会选择节点$n^{\prime }$而不是节点$t$

根据上述分析，可知算法会选择最短路上的节点而不是其他节点，在目标节点处结束所得路径一定是最短路。

三、一致性

3.1、一致性说明

实际问题对$\hat{h}(n)$存在一定的限制，使用不等式进行描述

假设对于任意节点$m$、$n$，均满足$h(m,n)+\hat{h}(n)\ge \hat{h}(m)$ 且 $h(n,m)+\hat{h}(m)\ge \hat{h}(n)$，即$\hat{h}(n)$满足一致性要求（consistency assumption）

式中，$h(m,n)$表示最优路径上节点$m$、$n$之间的成本

说明：论文中讨论了实际问题对于$\hat{h}(n)$的约束，得到结论$\hat{h}(n)=\underset{\theta \in {\Theta }_n}{\inf }{h}_{\theta }(n)$
（该部分内容详见论文III.ON THE OPTIMALITY OF A*——A. Limitation of Subgraphs by Information from the Problem）

一致性意味着节点经过其他节点到目标节点的成本不低于直接到目标节点的成本（一种简单但不严谨的理解：“三角形两边之和大于第三边”），可参考该链接加深对一致性的理解：

人工智能中A*算法的启发式的一致性有什么意义？ - Hepta的回答 - 知乎https://www.zhihu.com/question/23052955/answer/1648645823

考虑一致性之后，设计$\hat{h}(n)$的注意事项

• 所有节点采用一致的计算方法，不同节点的计算复杂性不一致（某些节点采用更复杂的计算方式），都可能违反一致性假设；
• 考虑节点状态，要求节点状态与所研究的问题相关，例如实际问题是确定路网中节点间的最短路，那么使用节点的坐标计算$\hat{h}(n)$就比较合适

• 以上图为例进行说明：
  • $\hat{h}(n)$​采用该计算方式：对于奇数节点，为节点到目标节点的直线距离；对于偶数节点，直接取1；
  • 对于开始节点，$\hat{f}(S)=\hat{h}(S)=8$；
  • 对于节点$n_2$，$\hat{h}(n_2)=1$，则$\hat{f}(n_2)=6+1=7$；
  • 对于节点$n_3$，$\hat{h}(n_3)=5$，则$\hat{f}(n_3)=3+5=8$；
  • 因为$\hat{f}(n_2)<\hat{f}(n_3)$，因此下一步会拓展节点$n_2$（错误拓展），因为此时$h(S,n_2)+\hat{h}(n_2)=6+1<\hat{h}(S)=8$，不符合一致性假设；
  • 实例中根据节点索引的奇偶性（与节点状态无关）确定$\hat{h}(n)$，导致其不符合一致性假设

3.2、相关引理及推论

3.2.1、引理2证明

引理2：若$\hat{h}(n)$满足一致性，则A*算法执行过程中进行拓展的节点$n$都满足$\hat{g}(n)=g(n)$

意味着节点$n$​一旦closed就不会再reopen，因此算法步骤4可简化

证明思路：反证法，即假设拓展节点$n$时，$\hat{g}(n)>g(n)$​

假设开始节点$S$到节点$n$之间存在最短路$P$，根据引理1，此时（选择节点$n$进行拓展的时刻）$P$上存在一个节点$n^{\prime }$，满足$\hat{g}(n^{\prime })=g(n^{\prime })$

case1：节点$n^{\prime }=n$，则引理2成立

case2：节点$n^{\prime }\ne n$

• 因为$\hat{g}(n)>g(n)$，所以$S$到$n$暂未找到最优路径

• $\hat{g}(n)>g(n)=g(n^{\prime })+h(n^{\prime },n)=\hat{g}(n^{\prime })+h(n^{\prime },n)$

• 两边同时加上$\hat{h}(n)$可得$\hat{g}(n)+\hat{h}(n)>\hat{g}(n^{\prime })+h(n^{\prime },n)+\hat{h}(n)\ge \hat{g}(n^{\prime })+\hat{h}(n^{\prime })$

• 即$\hat{f}(n)>\hat{f}(n^{\prime })$，与选择节点$n$而不是$n^{\prime }$进行拓展的事实矛盾，因此假设不成立

因此，引理2成立

3.2.2、引理3证明

引理3：若$\hat{h}(n)$满足一致性，则评估函数$\hat{f}(n)$单调不减，即若节点$p$先于节点$q$被拓展，则$\hat{f}(p)\le \hat{f}(q)$

证明思路：只需证明相邻两个被拓展的节点（例如节点$m$拓展之后就拓展节点$n$）满足该不等式，就可以证明引理成立

case1：开始节点$S$到节点$n$的最短路不经过节点$m$，则拓展节点$m$的时候，节点$n$可选，显然$\hat{f}(m)\le \hat{f}(n)$​

case2：开始节点$S$到节点$n$的最短路经过节点$m$，则$g(n)=g(m)+h(m,n)$

• 由引理2可知，$g(n)=\hat{g}(n)$，$g(m)=\hat{g}(m)$
• $\hat{f}(m)=\hat{g}(m)+\hat{h}(m)=g(m)+\hat{h}(m)\le g(m)+h(m,n)+\hat{h}(n)=g(n)+\hat{h}(n)=\hat{g}(n)+\hat{h}(n)=\hat{f}(n)$​
• 两两相邻的节点都满足不等式，则$\hat{f}(p)\le \hat{f}(q)$

因此，引理3成立

3.2.3、推论证明

推论：若节点$n$被拓展，则$\hat{f}(n)\le f(S)$

证明：

设目标节点为$t$，则基于引理3可知$\hat{f}(n)\le \hat{f}(t)$

因为$\hat{f}(t)=\hat{g}(t)+0=g(t)=f(t)=f(S)$

所以$\hat{f}(n)\le f(S)$

因此，推论成立

四、A*最优性

说明：该部分内容详见论文III.ON THE OPTIMALITY OF A*——C. Proof of the Optimality of A*

【读了几天都没完全想明白(-_-)，仅贴出来原文证明，及存在疑问的地方，希望大家能在评论区多交流，期待有研究者能答疑解惑】

4.1、最优性说明

对于一个满足可采纳性的算法A，如果它不能比A*算法获取更多关于图的信息，可称其为no more informed，则任意被A*拓展的节点都会被A拓展

（对于一个图/问题，可以设计不同的算法$\hat{h}(n)$使其满足可采纳性，即A算法可以看作是一个包含多个算法的集合，其中的最优算法为A*算法，其拓展的节点数最少）

4.2、相关定理及推论

4.2.1、定理2证明

定理2的成立有三个前提条件：

• 算法A是任何满足可采纳性的算法，且no more informed than A*；
• 若节点$n\ne m$，则$\hat{f}(n)\ne \hat{f}(m)$；<==？？？没有搞懂这个因果关系为什么成立？？？
• A*算法的$\hat{h}(n)$函数满足一致性假设。

证明思路：

• 首先证明特殊情况下该定理成立，原文描述：We prove this theorem for the special case for which ties never occur in the value of$\hat{f}(n)$​used by A*<==？？？没有搞懂这个ties的含义，前文并没有相关的解释！！！
• 其次将定理推广到更广的场景（定理3），原文描述：Later we shall generalize the theorem to cover the case where ties can occur

证明过程中再次强调了Strict inequality occurs because no ties are allowed，即在no ties的情况下，一致性原则为 $h(n,m)+\hat{h}(m)>\hat{h}(n)$

定理2的推论

与其他可采纳的A算法相比，A*是最优的算法，因为其找最短路的过程中拓展的节点数最少

4.2.2、定理3证明

4.2.3、推论证明

推论1：

推论2：

五：疑问汇总

• III.ON THE OPTIMALITY OF A*——A. Limitation of Subgraphs by Information from the Problem，提到了we have information from the problem that constrains the set$G_n$of possible subgraphs at each node，这里的子图似乎与物理上的子图（由节点及其相邻节点组成）含义不同，而与$\hat{h}(n)$有关；
• 定理2成立的前提条件中，若节点$n\ne m$，则$\hat{f}(n)\ne \hat{f}(m)$为何成立，即在no ties的情况下，一致性原则为何严格不等 $h(n,m)+\hat{h}(m)>\hat{h}(n)$