确知数字信号的最佳接收机

数字信号的统计特性

这一步意义在于确定接收电压的具体概率密度表达式，其后代入求误码率的具体表达式

高斯白噪声的k维联合概率密度

高斯白噪声满足高斯分布，且不同时刻相互独立
$$f_x(x)=\frac{1}{\sqrt{2\pi }\delta }exp[-\frac{(x-m{)}^2}{2{\delta }^2}]$$
在一个码元内有$k$个采样点，码元的持续时间$T_B$，以奈奎斯特速率$2f_H$采样，有$$k=2f_H{T}_B$$（限带）带宽为$f_H$

其k维联合概率密度函数为（n为变量，期望为零）
$$\begin{array}{rl}{f}_k(\vec{n})=& f_k(n_1,n_2,...,n_i,...,n_k)=f_k(n_1)f_k(n_2)...f_k(n_i)...f_k(n_k)\\ =& \frac{1}{(\sqrt{2\pi }\delta {)}^k}exp[-\frac{1}{2{\delta }_n^2}\sum _{j=1}^k{n}_j^2]\\ =& \frac{1}{(\sqrt{2\pi }\delta {)}^k}exp[-\frac{1}{2n_0{f}_H}\sum _{j=1}^k{n}_j^2]\end{array}$$
$\vec{n}$是一个k维向量，对应k个采样点

高斯白噪声的数学期望$m_n=0$，方差${\delta }_n^2=n_0{f}_H$
$n_0$为噪声单边功率谱密度

将码元内平均功率（离散采样点功率累加）写成积分式
$$\begin{array}{rl}& \frac{1}{k}\sum _{j=1}^k{n}_j^2=\frac{1}{2f_H{T}_B}\sum _{j=1}^k{n}_j^2\\ =& \frac{1}{T_B}{\int }_0^{T_B}{n}^2(t)dt\end{array}$$

故$$\sum _{j=1}^k{n}_j^2=2f_H{\int }_0^{T_B}{n}^2(t)dt$$
代入$f_k(\vec{n})$有
$$f_k(\vec{n})=\frac{1}{(\sqrt{2\pi }\delta {)}^k}exp[-\frac{1}{n_0}{\int }_0^{T_B}{n}^2(t)dt]$$

接收端电压的k维联合概率密度

在带限高斯白噪声的推导中仅将“信号”部分由离散形式变换成了连续积分形式，因此可以将结果套用到不同的信号中去

接收端电压信号$$r(t)=s(t)+n(t)$$$s(t)$为确定信号，$n(t)$为随机过程，则$r(t)$仍然为随机过程和高斯分布

$E[r(t)]=s(t)$
方差仍为${\delta }_n^2$

故直接根据高斯分布修改结果变量即可

二进制信号码元为$s_0(t)$和$s_1(t)$，抽样点矢量为$\vec{s}$

则接收端的抽样点矢量$$\vec{r}=\vec{s}+\vec{n}$$还是k个点

按出现的码元分两个情况考虑

• 当出现的信号为$s_0(t)$$$f_0(\vec{r})=\frac{1}{(\sqrt{2\pi }\delta {)}^k}exp[-\frac{1}{n_0}{\int }_0^{T_B}[r(t)-s_0(t){]}^{2}dt]$$$r(t)$为当前高斯变量，$s_0(t)$为均值，套入公式
• 当出现的信号为$s_1(t)$$$f_1(\vec{r})=\frac{1}{(\sqrt{2\pi }\delta {)}^k}exp[-\frac{1}{n_0}{\int }_0^{T_B}[r(t)-s_1(t){]}^{2}dt]$$

---

数字信号的最佳接收

这一步在于求出使得总误码率最小的最佳判决门限的通式

判决门限电平为$\overrightarrow{{r_0}^{\prime }}$ ，为k维矢量

二进制系统当接收端电压信号$\vec{r}<\overrightarrow{{r_0}^{\prime }}$，判为0 ; $\vec{r}>\overrightarrow{{r_0}^{\prime }}$，判为1

联合概率密度函数（似然函数）$f_0(\vec{r})$和$f_1(\vec{r})$

总误码率$$\begin{array}{rl}{P}_e=& P(1)P(0/1)+P(0)P(1/0)\\ =& P(1){\int }_{-\infty }^{\overrightarrow{{r_0}^{\prime }}}{f}_1(\vec{r})d\vec{r}+P(0){\int }_{\overrightarrow{{r_0}^{\prime }}}^{\infty }{f}_0(\vec{r})d\vec{r}\end{array}$$
使得$P_e$（关于$\overrightarrow{{r_0}^{\prime }}$的函数）最小的极值点$\overrightarrow{r_0}$处满足$$\frac{\partial P_e}{\partial \overrightarrow{{r_0}^{\prime }}}{|}_{\overrightarrow{{r_0}^{\prime }}=\overrightarrow{r_0}}=0$$
有（最佳接收准则） $$P(1)f_1(\overrightarrow{r_0})-P(0)f_0(\overrightarrow{r_0})=0$$

最大似然准则

• $\frac{f_0(\vec{r})}{f_1(\vec{r})}>\frac{P(1)}{P(0)},判为0$
• $\frac{f_0(\vec{r})}{f_1(\vec{r})}<\frac{P(1)}{P(0)},判为1$

即

• $$P(0)f_0(\vec{r})>P(1)f_1(\vec{r}),判为0$$
• $$P(0)f_0(\vec{r})<P(1)f_1(\vec{r}),判为1$$

发送先验概率等概$P(0)=P(1)$时

• $$f_0(\vec{r})>f_1(\vec{r}),判为0$$
• $$f_0(\vec{r})<f_1(\vec{r}),判为1$$

最大后验概率准则

与最大似然准则等价

$f_r(0)$ : 收到$\vec{r}$后发送0的概率 $P(0/\vec{r})$
$f_r(1)$ : 收到$\vec{r}$后发送1的概率 $P(1/\vec{r})$

确知数字信号的最佳接收（相关接收法）

在《数字信号的最佳接收》中讨论得到了最佳误码率时门限电平与数字信号（0和1）的概率密度函数的关系，由此得到了最佳接收准则及相应的判决准则

在《数字信号的统计特性》中求出了二进制信号的具体概率密度函数

因此将具体的概率密度函数代入最佳接收准则中可以构造出二进制确知数字信号的最佳接收机

假设（前提）：

• 两码元$s_0(t)$与$s_1(t)$能量相等
• ${\int }_0^{T_B}{s}_0^2(t)dt={\int }_0^{T_B}{s}_1^2(t)dt$
• 其余则与《数字信号的统计特性》中的设定相同

代入结果经过两边取对数和化简得

• $$W_0+{\int }_0^{T_B}r(t)s_0(t)dt>W_1+{\int }_0^{T_B}r(t)s_1(t)dt,判为0$$
• $$W_0+{\int }_0^{T_B}r(t)s_0(t)dt<W_1+{\int }_0^{T_B}r(t)s_1(t)dt,判为1$$
  其中$W_0=\frac{n_0}{2}lnP(0)$，$W_1=\frac{n_0}{2}lnP(1)$，可看作是加权（weight）因子，若两码元等概发送（先验概率相等），二进制确知信号最佳接收准则可丢去加权因子

式子也可以看作是$r(t)$和$s_0(t)$、$s_1(t)$作相关运算，称作相关接收法

确知二进制信号的最佳接收机误码率

误码率$$P_e=P(0)P(1/0)+P(1)P(0/1)$$
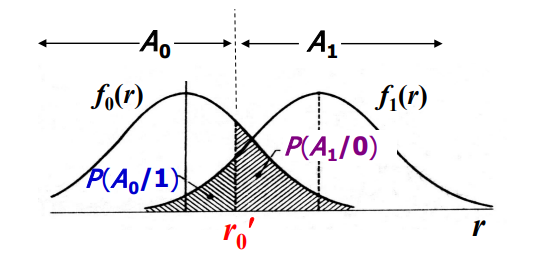
$P(1/0)$是发送0而判决为1的概率，实质上求法与数字基带系统的误码率相同（根据两个信号的高斯分布图直观可判断），

但由于本身两个接收信号是随机过程，又要求的是最佳接收下的误码率，判决门限此前没有研究具体形式，积分表达式不好表达，

就直接使用最佳接收准则的公式进行计算

（将错误实际的接收$r(t)$代入）来得到结果，形式上还是使用高斯变量的图直观得到）

经繁琐的推导计算得$$P(0/1)=P(\xi <a)=\frac{1}{\sqrt{2\pi }{\delta }_{\xi }}{\int }_{-\infty }^a{e}^{-\frac{x^2}{2{\delta }_{\xi }^2}}$$
$\xi$为高斯随机变量（${\int }_0^{T_B}n(t)[s_1(t)-s_0(t)]dt$）

需要使用的两个值：
$$a=\frac{n_0}{2}ln\frac{P(0)}{P(1)}-\frac{1}{2}{\int }_0^{T_B}[s_1(t)-s_0(t){]}^{2}dt$$
$${\delta }_{\xi }^2=\frac{n_0}{2}{\int }_0^{T_B}[s_1(t)-s_0(t){]}^{2}dt$$
还有$$P(1/0)=P(\xi <b)=\frac{1}{\sqrt{2\pi }{\delta }_{\xi }}{\int }_{-\infty }^b{e}^{-\frac{x^2}{2{\delta }_{\xi }^2}}$$
$$b=\frac{n_0}{2}ln\frac{P(1)}{P(0)}-\frac{1}{2}{\int }_0^{T_B}[s_1(t)-s_0(t){]}^{2}dt$$

先验概率相等时的误码率

当先验概率相等$P(0)=P(1)=\frac{1}{2}$时，$$c=a=b=-\frac{1}{2}{\int }_0^{T_B}[s_1(t)-s_0(t){]}^{2}dt$$
$$P_e=\frac{1}{\sqrt{2\pi }{\delta }_{\xi }}{\int }_{-\infty }^c{e}^{-\frac{x^2}{2{\delta }_{\xi }^2}}$$
$c$为常数，与两个码元波形之差有关，与波形无关

故先验概率相等时，误码率仅与两种码元波形之差的能量有关，
差别越大，$c$越小（有负号），误码率越小

码元互相关系数

为简便计算，误码率与两码元波形差即相关性有关

引入相关系数$$\rho =\frac{{\int }_0^{T_B}{s}_0(t)s_1(t)dt}{\sqrt{E_0{E}_1}}$$
而在前提中码元能量相同，$E_0=E_1=E_b={\int }_0^{T_B}{s}_b^2(t)dt$
故$$\rho =\frac{{\int }_0^{T_B}{s}_0(t)s_1(t)dt}{E_b}$$ $${\int }_0^{T_B}[s_0^2(t)+s_1^2(t)]dt=2E_b$$$$\begin{array}{rl}c=& -\frac{1}{2}{\int }_0^{T_B}[s_1(t)-s_0(t){]}^{2}dt\\ =& -\frac{1}{2}{\int }_0^{T_B}[s_0^2(t)+s_1^2(t)]dt+{\int }_0^{T_B}{s}_0(t)s_1(t)dt\\ =& -E_b(1-\rho )\end{array}$$
经变量代换和计算得$$P_e=\frac{1}{2}erfc(\sqrt{\frac{E_b(1-\rho )}{2n_0}})$$
其中
$$\begin{array}{rl}\frac{E_b}{n_0}=& \frac{P_s{T}_B}{n_0}=\frac{P_s}{n_{0}B}(B=\frac{1}{T_B})\\ =& \frac{P_s}{P_n}\end{array}$$可以表示信噪比

故最佳接收性能只与信号信噪比与相关系数有关

---

非确知信号的最佳接收

随相信号的最佳接收

随相信号的相位为随机变量，这里选取2FSK信号研究，要求两个码元等概、等能、正交
$$s_0(t,{\varphi }_0)=Acos(w_{0}t+{\varphi }_0)$$
$$s_1(t,{\varphi }_1)=Acos(w_{0}t+{\varphi }_1)$$
这里${\varphi }_0$和${\varphi }_1$为随机变量，对应两个码元不同的随机过程

对推导过程的解释：
知道给定相位后的概率密度函数$f_i(r/{\varphi }_i)$。但是想要套用确定信号的最佳接收准则需要有$f_0(r)$和$f_1(r)$，这里对应的是$f_0(r,{\varphi }_0)$，$f_1(r,{\varphi }_1)$

• $$M_0^2>M_1^2,判为0$$
• $$M_0^2<M_1^2,判为1$$

这里$$M_0=\sqrt{X_0^2+Y_0^2}$$ $$M_1=\sqrt{X_1^2+Y_1^2}$$$$X_0={\int }_0^{T_B}r(t)cos{w}_{0}tdt$$ $$Y_0={\int }_0^{T_B}r(t)sin{w}_{0}tdt$$$$X_1={\int }_0^{T_B}r(t)cos{w}_{1}tdt$$ $$Y_1={\int }_0^{T_B}r(t)sin{w}_{1}tdt$$
可以看出不需要接收机端不需要码元信号$s_0(t)$和$s_1(t)$，为非相干接收

误码率$$P_e=\frac{1}{2}{e}^{-\frac{E_b}{2n_0}}$$

起伏信号的最佳接收

幅度和相位均为随机变量

---

数字信号的匹配滤波接收

目的：接收信号通过滤波器，使得在抽样时刻时滤波器的输出信号的信噪比最大（最大化抽样时刻信号的信噪比）

滤波器$H(w)$称为匹配滤波器，使输出信噪比最大

输出的最大信噪比及条件

滤波器输入电压$$r(t)=s(t)+n(t),0\le t\le T_B$$
高斯白噪声$n(t)$的单边功率谱密度为$n_0$，则双边谱密度为$$P_n(f)=\frac{n_0}{2}$$
经过滤波器后输出电压$$y(t)=s_o(t)+n_o(t)$$
由于通过线性系统时输出功率谱密度$$P_y(f)=P_r(f)|H(f){|}^2$$等于输入功率谱密度乘以滤波器系统函数模的平方

输出噪声的功率为$$N_o=\frac{n_0}{2}{\int }_{-\infty }^{\infty }|H(f){|}^{2}df$$
在抽样时刻$t_0$输出信号$s_o(t_0)$的瞬时功率为$|s_0(t_0){|}^2$

而$$S_o(f)=S(f)H(f)$$ 那么$$s_o(t)=F{T}^{-1}[S_o(f)]={\int }_{-\infty }^{\infty }H(f)S(f)e^{j2\pi ft}df$$ 注意是$f$不是角频率

则$$|s_0(t_0){|}^2=|{\int }_{-\infty }^{\infty }H(f)S(f)e^{j2\pi f{t}_0}df{|}^2$$
输出信号信噪比$$\begin{array}{rl}{r}_0=& \frac{|s_0(t_0){|}^2}{N_o}\\ =& \frac{|{\int }_{-\infty }^{\infty }H(f)S(f)e^{j2\pi f{t}_0}df{|}^2}{\frac{n_0}{2}{\int }_{-\infty }^{\infty }|H(f){|}^{2}df}\\ \le & \frac{{\int }_{-\infty }^{\infty }|H(f){|}^{2}df{\int }_{-\infty }^{\infty }|S(f){|}^{2}df}{\frac{n_0}{2}{\int }_{-\infty }^{\infty }|H(f){|}^{2}df},Schawrtz不等式\\ =& \frac{{\int }_{-\infty }^{\infty }|S(f){|}^{2}df}{\frac{n_0}{2}}\\ =& \frac{2E}{n_0}\end{array}$$
其中
$$E={\int }_{-\infty }^{\infty }|S(f){|}^{2}df$$为信号码元的能量

最佳接收滤波器传输特性

仅当$H(f)=k{S}^{\ast }(f)e^{-j2\pi f{t}_0}$时取等号

冲激响应$$h(t)=F{T}^{-1}[H(f)]=ks(t_0-t)$$ 等于码元信号的翻折后向右移动$t_0$

因为要求为物理可实现，即因果系统，故要求
$$h(t)=ks(t_0-t)=0,t<0$$
代换有$$s(t)=0,t>t_0$$ 即接收后接要立刻清零

选取码元结束时刻抽样$t_0=T_B$

相关形式

$$h(t)=ks(T_B-t)$$
输出信号$$\begin{array}{rl}{s}_o(t)=& s(t)\ast h(t)=s(t)\ast [ks(T_B-t)]\\ =& k{\int }_{-\infty }^{\infty }s(x)s(x+t-t_0)dx，变量代换后\\ =& kR(t-t_0)\end{array}$$

输出信号为其自相关函数的k倍，对比$s_o(t)={\int }_{-\infty }^{\infty }H(f)S(f)e^{j2\pi ft}df$，两个不同域的表达形式

可以看作是一个相关器

一般可取$k=1$，则$$s_0(t_0)=R(0)={\int }_{-\infty }^{\infty }s(t{)}^{2}dt=E,Parseval定理$$

积分形式

也可以交换卷积的次序写作$$s_o(t)={\int }_{-\infty }^{\infty }s(\tau )h(t-\tau )d\tau$$
其中$$h(t)=ks(T_B-t)$$

输出电压及系统框图

考虑滤波器的输出电压$$y(t)=s_o(t)+n_o(t)$$ 类比上面$s_o(t)$的积分形式
$$\begin{array}{rl}y(t)=& r(t)\ast h(t)\\ =& k{\int }_{-\infty }^{\infty }r(u)s(T_B-t+u)du\\ =& k{\int }_{t-T_B}^{t}r(u)s(T_B-t+u)du\end{array}$$
积分限需满足s的范围在$[0,T_B]$区间（满足因果性）

抽样时刻$t=T_B$时
$$y(T_B)=k{\int }_0^{T_B}r(u)s(u)du$$
与相关接收法表达式相同

故当$t=T_B$时匹配滤波器法和相关接受法等效为最佳接收法，实现了误码率最小和信噪比最大的“最佳”规则的等效

---

随相信号和起伏信号也可以使用匹配滤波器法接收，这里不再展开