【brainpy学习笔记】突触可塑性模型1——STP/STDP模型

在生物体中，神经元之间的连接强度会随着时间变化，这种性质被称为突触可塑性。也就是说，刺激的时间不同，即使刺激的类型的强度相同，也会在突触后膜上产生不同的电流效应。根据连接强度变化维持的时长，将突触可塑性分为短时程可塑性与长时程可塑性。本文介绍了短时程可塑性模型STP与脉冲时序依赖可塑性STDP模型。

Fellyhosn

4546人浏览 · 2023-05-10 19:19:24

Fellyhosn · 2023-05-10 19:19:24 发布

参考书目：《神经计算建模实战——基于brainpy》吴思

0 引言

前面两篇笔记介绍的突触模型都是静态的，即两个神经元之间的连接权重不变。但是在生物体中，神经元之间的连接强度会随着时间变化，这种性质被称为突触可塑性。也就是说，刺激的时间不同，即使刺激的类型的强度相同，也会在突触后膜上产生不同的电流效应。

这种可塑性被认为是学习、记忆、实时计算等功能的核心的神经基础。（例如在学习同一知识点时，第二次学习比第一次更轻松，因为这个知识点对应的突触的连接强度增强，使得第二次学习产生的突触后电流强度低于第一次的，所谓熟能生巧也是这个道理）

根据连接强度变化维持的时长，将突触可塑性分为短时程可塑性与长时程可塑性。下面将分别介绍其模型。

1 突触短时程可塑性

1.1 短时程可塑性介绍

突触短时程可塑性指的是突触的连接强度在毫秒到秒级发生变化。在反复刺激下突触后神经元在短时间内减弱/增强的现象被称为短时程抑制（STD）/短时程增强（STF）。突触短时程可塑性模型（STP）在突触模型中融合了STD与STF。

1.2 STP模型

STF与STD的建模要从其生理机制入手，思考为什么会出现短时程抑制/短时程增强？一般来说，短时程增强的原因是突触前脉冲让突触前神经元释放了更大比例的神经递质，即神经递质的释放概率增加；而短时程抑制的原因是由于神经递质的损耗。用u和x分别表示这两种影响因子，即u表示神经递质的释放概率，x表示突触前膜中神经递质的剩余比例，它们的取值范围都是[0,1]。u和x的每一次跳变都是由于脉冲释放神经递质引起的，用 $x^-,u^+$ 表示x在这一时刻跳变前、u在这一时刻跳变后的值， $x^-\cdot u^+$ 表示了突触前膜在这一次脉冲下释放的神经递质的比例。短时程可塑性模型表达式如下：

$\left\{\begin{matrix} \frac{du}{dt}=-\frac{u}{\tau_f}+U(1-u^-)\displaystyle\sum_{t^{(f)}}\delta(t-t^{(f)}) \\ \frac{dx}{dt}=\frac{1-x}{\tau_d}-u^+x^-\displaystyle\sum_{t^{(f)}}\delta(t-t^{(f)}) \\ \frac{dg}{dt}=\frac{g}{\tau}+\bar{g}u^+x^-\displaystyle\sum_{t^{(f)}}\delta(t-t^{(f)}) \end{matrix}\right.$

第一个式子对u进行建模， $\tau_f$ 为u的衰减系数，在正常情况下，u以 $\tau_f$ 为时间常数衰减到0，每次更新时增加 $U(1-u^-)$ ，u越大其增量越小，U表示最大增量，其取值范围也是[0,1]。

第二个式子对x进行建模， $\tau_d$ 为x的衰减系数，在正常情况下，x以 $\tau_d$ 为时间常数增加到1，每次更新时减少 $u^+x^-$ （此时比例为 $u^+x^-$ 的神经递质被释放）。

第三个式子对电导g进行建模，沿用了指数衰减模型中的微分方程， $\tau_d$ 为g的衰减系数， $\bar{g}$ 为最大电导，乘以 $u^+x^-$ 便得到了g的增量。

在该模型中，u主要贡献短时程增强的效果，其初始值为0并逐渐升高；x主要贡献短时程抑制的效果，其初始值为1并逐渐降低。时间常数 $\tau_f$ 与 $\tau_d$ 的大小关系决定了可塑性的最终效果。

用brainpy实现STP代码如下：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class STP(bp.dyn.TwoEndConn):
    def __init__(self,pre,post,conn,g_max=0.1,U=0.15,tau_f=1500.,tau_d=200.,
                 tau=8.,E=1.,delay_step=2,method='exp_auto',**kwargs):
        super(STP,self).__init__(pre=pre,post=post,conn=conn,**kwargs)
        self.tau_d = tau_d
        self.tau_f = tau_f
        self.tau = tau
        self.U = U
        self.g_max = g_max
        self.E = E
        self.delay_step = delay_step
        self.pre_ids,self.post_ids = self.conn.require('pre_ids','post_ids')
        num = len(self.pre_ids)
        self.x = bm.Variable(bm.ones(num))
        self.u = bm.Variable(bm.zeros(num))
        self.g = bm.Variable(bm.zeros(num))
        self.delay = bm.LengthDelay(self.g,delay_step)
        self.integral = bp.odeint(method=method,f=self.derivative)

    @property
    def derivative(self):
        du = lambda u,t:-u/self.tau_f
        dx = lambda x,t:(1-x)/self.tau_d
        dg = lambda g,t:-g/self.tau
        return bp.JointEq([du,dx,dg])
    def update(self,tdi):
        t,dt = tdi.t,tdi.dt
        delayed_g = self.delay(self.delay_step) #将g的计算延迟delay_step步长
        post_g = bm.syn2post(delayed_g,self.post_ids,self.post.num)
        self.post.input+=post_g*(self.E - self.post.V_rest)
        syn_sps = bm.pre2syn(self.pre.spike,self.pre_ids) #记录哪些突触前神经元产生了脉冲
        u,x,g = self.integral(self.u,self.x,self.g,t,dt)
        u = bm.where(syn_sps,u+self.U*(1-self.u),u)
        x = bm.where(syn_sps,x-u*self.x,x)
        g = bm.where(syn_sps,g+self.g_max*u*self.x,g)
        self.u.value,self.x.value,self.g.value = u,x,g
        self.delay.update(self.g)

def run_STP(title='STP model',**kwargs):
    neu1 = bp.dyn.LIF(1)
    neu2 = bp.dyn.LIF(2)
    syn = STP(neu1,neu2,bp.connect.All2All(),**kwargs)
    net = bp.dyn.Network(pre=neu1,syn=syn,post=neu2)
    #输入分段电流
    inputs,dur = bp.inputs.section_input(values=[22.,0.,22.,0],
                                         durations=[200.,200.,25.,75.],
                                         return_length=True)
    runner = bp.dyn.DSRunner(net,inputs=[('pre.input',inputs,'iter')],monitors=['syn.u','syn.x','syn.g'])
    runner.run(dur)
    fig,gs=plt.subplots(2,1,figsize=(6,4.5))
    plt.sca(gs[0])
    plt.plot(runner.mon.ts,runner.mon['syn.x'][:,0],label='x',color='b')
    plt.plot(runner.mon.ts,runner.mon['syn.u'][:,0],label='u',color='y',linestyle='--')
    plt.legend(loc='center right')
    plt.title(title)
    plt.sca(gs[1])
    plt.plot(runner.mon.ts,runner.mon['syn.g'][:,0],label='g',color='r')
    plt.legend(loc='center right')
    plt.xlabel('t[ms]')
    plt.tight_layout()
    plt.show()
run_STP(title='STF',U=0.1,tau_d=15.,tau_f=200.)
run_STP(title='STD',U=0.4,tau_d=200.,tau_f=15.)

该代码模拟了一个突触前神经元和一个突触后神经元，神经元采用LIF模型，输入分段电流，并查看x,u,g的变化情况。使用pre2syn函数记录产生脉冲的突触前神经元。通过控制 $U,\tau_f,\tau_d$ 的大小关系调整STF/STD模型，运行结果如下：

在第一次模拟中， $\tau_f$ 很大而 $\tau_d$ 很小，神经递质的存量x快速恢复，而释放概率u递减速度较慢，g在每次刺激后的增量变大，因此形成短时程增长STF。在200ms~400ms不发放脉冲时，u缓慢衰减，如果在下一次脉冲来临时u仍未衰减到0，则短时程增强的部分效果仍然保留，表现为g的增量大于第一次的增量。

在第一次模拟中， $\tau_d$ 很大而 $\tau_f$ 很小且U较大，神经递质的存量x恢复较满，而释放概率u递减速度较快，每次刺激后能释放的神经递质减少，因此形成短时程抑制STD。在200ms~400ms不发放脉冲时，x缓慢增加，如果在下一次脉冲来临时u仍未增加到1，则短时程抑制的部分效果仍然保留，表现为g的增量低于第一次的增量。

2 突触长时程可塑性

2.1 长时程可塑性介绍

短时程可塑性的持续时间较短，一般在毫秒级或秒级。短时程可塑性通常描述的是物理层面上的可逆变化，例如神经递质的消耗。而长时程可塑性的持续时间较长，通常在几十秒或更长，这意味着突触在生化层面已经发生了反应，最终改变了信号传递的强度。

我们在进行记忆时，通常会改变突触的信号传递强度（例如一个知识点反复记忆就可以形成长时记忆），神经科学家们普遍认为记忆就存储在神经元的连接之中，神经系统依靠突触的长时程可塑性来产生或者改变记忆。目前描述长时程可塑性的方式包括脉冲时序依赖可塑性，Hebb学习律，Oja法则和BCM法则等。

2.2 STDP模型

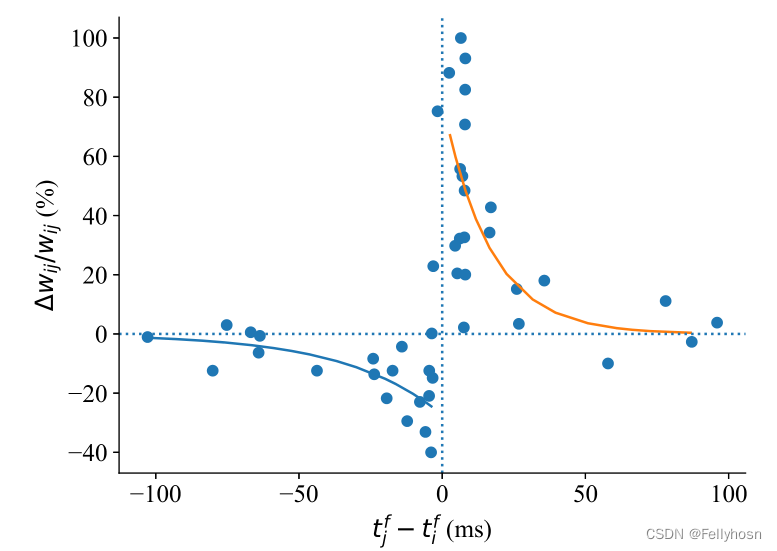
脉冲时序依赖可塑性（Spike-Timing-Dependent Plasticity）指的是突触前、后神经元发放脉冲的时间先后决定了突触连接强度的变化方式。记突触前神经元为j，突触后神经元为i，下图展示的是实验上观察到的STDP现象，横轴是 $t_j^f-t_i^f$ 表示突触前神经元和突触后神经元产生脉冲的时间差，纵轴表示突触权重的相对变化量：

位于0左侧的数据点表示突触前神经元先于突触后神经元发放，此时突触的权重增加，称为长时程增强LTP；位于0右侧的数据点表示突触后神经元比突触前神经元更先发放，此时权重增长为负，称为长时程抑制LTD。两个神经元发放的时间间隔越小，长时程增强/抑制的效果表现越明显。

这个图像可以被两条指数函数拟合： $\Delta w =\left\{\begin{matrix} A_1e^{-|\Delta t |/\tau_1},\Delta t <0 \\ -A_2e^{-|\Delta t |/\tau_2},\Delta t >0 \end{matrix}\right.$ ，其中A1与A2表示突触权重最大的改变量， $\tau_1,\tau_2$ 表示突触权重改变量随突触前后神经元的脉冲时差变化的时间常数。

STDP中对权重变化的建模不能采用上述的式子，因为突触前神经元一旦产生脉冲，其突触权重的变化必须综合考虑所有突触后神经元的历史脉冲，在大规模的脉冲神经网络中的实现是不现实的。通常的建模方式是用两个局部变量 $A_{pre}$ 与 $A_{post}$ 分别保存突触前和突触后神经元的脉冲发放所引起的突触强度变化 $\Delta w$ 的迹，最后两者相加便得到 $\Delta w$ 的变化。其数学表达式如下：

$\left\{\begin{matrix} \frac{dA_{pre}}{dt}=-\frac{A_{pre}}{\tau_1}+A_1\displaystyle\sum_{t_{pre}^{(f)}}\delta(t-t_{pre}^{(f)}) \\ \frac{dA_{post}}{dt}=-\frac{A_{post}}{\tau_2}+A_2\displaystyle\sum_{t_{post}^{(f)}}\delta(t-t_{post}^{(f)}) \\ \frac{dw}{dt}=-A_{post}\displaystyle\sum_{t_{pre}^{(f)}}\delta(t-t_{pre}^{(f)}) +A_{pre}\displaystyle\sum_{t_{post}^{(f)}}\delta(t-t_{post}^{(f)}) \end{matrix}\right.$

对于最后一个表达式：在突触前神经元产生动作电位时，突触权重的减少与突触后的迹 $A_{post}$ 成正比；而突触后神经元产生动作电位时，突触权重增强，与突触前的迹 $A_{pre}$ 成正比。

具体来说，当突触前神经元i发放一个脉冲时， $A_{pre}[i]$ 的值会增加一个常数 $A_1$ ，表示该神经元被激活的程度。而当突触后神经元j发放一个脉冲时， $A_{post}[j]$ 的值也会增加一个常数 $A_2$ 。因此， $A_{pre}$ 和 $A_{post}$ 的作用类似于突触前/后神经元活动的计数器，记录了神经元之间的同步激活情况。

突触权重w的更新取决于 $A_{pre}$ 和 $A_{post}$ 。当神经元i在时刻t发放一个脉冲时，其对应的突触权重w[i]会减去 $A_{post}[j]$ ，其中j是神经元i所连接的突触后神经元。这个规则的意义是，在突触后神经元发放脉冲之后，与其相连的突触权重应该减弱一定程度，避免过度强化表示相邻时间上的相关性。也就是说，当神经元j在时刻t'发放一个脉冲时，其对应的突触权重w[j]应该增加 $A_{pre}[i]$ ，表示突触前神经元与突触后神经元之间的相关性得到了加强。

对于电导g，仍然采用指数衰减模型。

用brainpy编写STDP代码如下：

import numpy as np
import brainpy as bp
import brainpy.math as bm
import matplotlib.pyplot as plt

class STDP(bp.dyn.TwoEndConn):
    def __init__(self,pre,post,conn,tau_1=16.8,tau_2=33.7,tau=8.,A_1=0.96,
                 A_2=0.53,E=1.,delay_step=0,method='exp_auto',**kwargs):
        super(STDP,self).__init__(pre=pre,post=post,conn=conn,**kwargs)
        self.tau_1 = tau_1
        self.tau_2 = tau_2
        self.tau = tau
        self.A_1 = A_1
        self.A_2 = A_2
        self.E = E
        self.delay_step = delay_step
        self.method = method
        self.pre_ids,self.post_ids = self.conn.require('pre_ids','post_ids')
        num = len(self.pre_ids)
        self.Apre = bm.Variable(bm.zeros(num))
        self.Apost = bm.Variable(bm.zeros(num))
        self.w = bm.Variable(bm.ones(num))
        self.g = bm.Variable(bm.zeros(num))
        self.delay = bm.LengthDelay(self.pre_ids,delay_step)#定义延迟处理器
        self.integral = bp.odeint(method=method,f=self.derivative)

    @property
    def derivative(self):
        dApre = lambda Apre,t: -Apre / self.tau_1
        dApost = lambda Apost,t: -Apost / self.tau_2
        dg = lambda g,t: -g / self.tau
        return bp.JointEq([dApre,dApost,dg])

    def update(self,tdi):
        t,dt = tdi.t,tdi.dt
        delayed_g = self.delay(self.delay_step)#将g的计算延迟delay_step步长
        post_g = bm.syn2post(delayed_g,self.post_ids,self.post.num)
        self.post.input += post_g * (self.E - self.post.V_rest)#计算突触后电流
        #记录哪些突触前/后神经元产生了脉冲
        pre_spikes = bm.pre2syn(self.pre.spike,self.pre_ids)
        post_spikes = bm.pre2syn(self.post.spike,self.post_ids)
        self.Apre.value,self.Apost.value,self.g.value = self.integral(self.Apre,self.Apost,self.g,t,dt)
        Apre = bm.where(pre_spikes,self.Apre+self.A_1,self.Apre)
        self.w.value = bm.where(pre_spikes,self.w - self.Apost,self.w)
        Apost = bm.where(post_spikes,self.Apost+self.A_2,self.Apost)
        self.w.value = bm.where(post_spikes,self.w + self.Apre,self.w)#更新权重
        self.Apre.value = Apre
        self.Apost.value = Apost
        self.g.value = bm.where(pre_spikes,self.g+self.w,self.g)
        self.delay.update(self.g) #更新延迟器
def run_STDP(I_pre,I_post,dur,**kwargs):
    pre = bp.neurons.LIF(1)
    post = bp.neurons.LIF(1)
    syn = STDP(pre,post,bp.connect.All2All(),**kwargs)
    net = bp.dyn.Network(pre=pre,syn=syn,post=post)
    runner = bp.dyn.DSRunner(net,inputs=[('pre.input',I_pre,'iter'),('post.input',I_post,'iter')],
                             monitors=['pre.spike','post.spike','syn.g','syn.w','syn.Apre','syn.Apost'])
    runner(dur)

    fig,gs = plt.subplots(5,1,gridspec_kw={'height_ratios':[2,1,1,2,2]},figsize=(6,8))
    plt.sca(gs[0])
    plt.plot(runner.mon.ts,runner.mon['syn.g'][:,0],label='$g$',color='r')
    plt.sca(gs[1])
    plt.plot(runner.mon.ts,runner.mon['pre.spike'][:,0],label='pre spike',color='g')
    plt.legend(loc='center right')
    plt.sca(gs[2])
    plt.plot(runner.mon.ts, runner.mon['post.spike'][:, 0], label='post spike', color='b')
    plt.sca(gs[3])
    plt.plot(runner.mon.ts, runner.mon['syn.w'][:, 0], label='$w$', color='m')
    plt.sca(gs[4])
    plt.plot(runner.mon.ts, runner.mon['syn.Apre'][:, 0], label='Apre', color='coral')
    plt.plot(runner.mon.ts, runner.mon['syn.Apost'][:, 0], label='Apost', color='gold')

    for i in range(4): gs[i].set_xticks([])
    #for i in range(1,3): gs[i].set_yticks([])
    for i in range(5): gs[i].legend(loc='upper right')

    plt.xlabel('t[ms]')
    plt.tight_layout()
    plt.subplots_adjust(hspace=0.)
    plt.show()
duration=300.
I_pre = bp.inputs.section_input([0,30,0,30,0,30,0,30,0,30,0,30,0],
                                [5,15,15,15,15,15,100,15,15,15,15,15,duration-255])
I_post = bp.inputs.section_input([0,30,0,30,0,30,0,30,0,30,0,30,0],
                                 [10,15,15,15,15,15,90,15,15,15,15,15,duration-250])
run_STDP(I_pre,I_post,duration)

仍然采用LIF模型建模突触前/后神经元，从t=5ms起，先给突前神经元一段大小为 30、持续时间为 15 ms 电流，让 LIF 模型产生一个脉冲，然后在 t=10 ms 再给突后神经元一个相同的输入，间隔 15 ms 后重复3次这就形成了突触前神经元早于突触后神经元发放的情形，即 $t_{pre}^{(f)}-t_{post}^{(f)}=-5$ 。在静息一个较长的时间间隔后，我们再把刺激顺序调整为 $t_{pre}^{(f)}-t_{post}^{(f)}=3$ ，观察连接重w及电导g的变化。