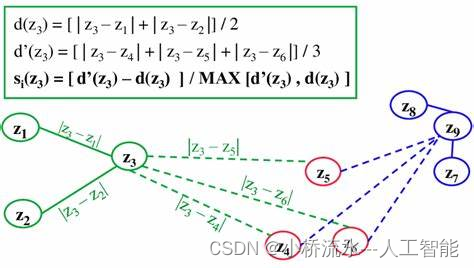
轮廓系数（Silhouette Coefficient）是一种评估聚类效果的指标，用来衡量数据点在聚类中的紧密程度和分离程度。每个数据点的轮廓系数是通过比较该点与其所在聚类内的点的平均距离（内聚度）和该点与最近的其他聚类中的点的平均距离（分离度）来计算的。轮廓系数的值范围从-1到1，其中接近1的值表示该点很好地匹配其自身聚类，并且与相邻聚类差异很大，而接近-1的值则表示该点更适合与相邻的聚类而不是当前聚类。

轮廓系数的计算步骤包括：

1. 对于每个样本点( i )：

   • 计算与同一聚类中所有其他点的平均距离，称为内聚度 ( a(i) )。
   • 对于每个其他聚类，计算点( i )到该聚类中所有点的平均距离，并取这些距离中的最小值，称为分离度 ( b(i) )。

2. 对于每个样本点( i )，轮廓系数 ( s(i) ) 由以下公式给出：
   $$s(i)=\frac{b(i)-a(i)}{\max (a(i),b(i))}$$

   其中：

   • ( a(i) ) 是点( i )与其同一聚类中所有其他点的平均距离。
   • ( b(i) ) 是点( i )与最近的其他聚类中所有点的平均距离。
   • 当只有一个样本在聚类中时，通常( s(i) = 0 )。

全局轮廓系数

全局轮廓系数是所有样本的轮廓系数( s(i) )的平均值，用来衡量整体聚类的质量。全局轮廓系数越接近1，说明聚类效果越好；接近-1则表明聚类效果较差；接近0表明聚类重叠严重。

这种方法特别有用于确定聚类的数量是否合适，或者比较不同聚类算法或参数设置的效果。在实际应用中，通过计算不同聚类结果的轮廓系数，可以选择一个最佳的聚类方案。