双曲嵌入深度学习

1. 双曲空间双曲空间的定义是曲率为负常数的一类空间。我们首先以一个图为例，来看欧式空间与双曲空间的区别。左图为欧式空间，我们从中间节点向外部移动，走一步所能达到的网格数量是323^232，两步是525^252，网络空间会随着半径多项式（平方）的关系进行增长。反观右侧的树结构空间，假设为二叉树，从中心点向外走的节点个数是呈指数增长的，因此这是一个呈指数增长的空间。假设右侧的树结构我们嵌入到欧式空间

Kanny广小隶

8097人浏览 · 2021-08-27 21:43:32

Kanny广小隶 · 2021-08-27 21:43:32 发布

1. 双曲空间

双曲空间的定义是曲率为负常数的一类空间。我们首先以一个图为例，来看欧式空间与双曲空间的区别。

左图为欧式空间，我们从中间节点向外部移动，走一步所能达到的网格数量是 $3^2$ ，两步是 $5^2$ ，网络空间会随着半径多项式（平方）的关系进行增长。反观右侧的树结构空间，假设为二叉树，从中心点向外走的节点个数是呈指数增长的，因此这是一个呈指数增长的空间。

假设右侧的树结构我们嵌入到欧式空间上，那么红色的节点到绿色的节点在树上的距离相距 $8$ 个结点，但直接在平面上看两个节点非常近。一个好的嵌入实际上是需要保距的，这时我们就可以在原本的欧式空间上引进曲率，将原本的平面转化为曲面。

1）曲率（Curvature）

曲率是描述几何体弯曲程度的量，例如曲面偏离平面的程度，或者曲线偏离直线的程度。

直线的曲率为 $0$ ；圆为常数曲率（即每一点的曲率都是一样的），半径的导数为其曲率，圆越小，曲率越大。而抛物线有曲率，但每一点的曲率都不一致。

正负曲率可通过如下几何方式解释：

正曲率：曲面上的三角形的内角和大于 $\pi$ 。
负曲率：负曲率曲面上的三角形的内角和小 $\pi$ 。

下面的马鞍面为负曲率曲面：

双曲空间是曲率为负常数的一类空间，双曲空间随着半径增大呈现指数扩展，它可以看成是连续的树结构空间。这种特性与理论和现实中的很多现象相符合，使得双曲空间具有广阔的应用。

为了更详细地介绍双曲空间，我们首先引入一个新的概念：度规张量。

2）度规张量（Metric tensor）

在黎曼几何里面，度量张量又叫黎曼度量，物理学译为度规张量，是指一用来衡量度量空间中距离，面积及角度的二阶张量。本质上是将集合中⼀对元素映射为实数的映射。其可以在任意⼀个曲⾯（流形）的切向量空间中定义度规，该度规将两个向量映射为⼀个实数，度规实际上可以看作是对向量的内积以及距离等概念的推广，它是一种双线性函数。

当选定一个局部坐标系统 $x^{i}$ ，度量张量为二阶张量一般表示为 $ds^2=\sum_{ij}g_{ij}dx^i dx^j$ ，给定一组基后，也可以用矩阵 $g_{ij})$ 表示，记作为 $G$ 或 $g$ 。而 $g_{{ij}}$ 记号传统地表示度量张量的协变分量（亦为“矩阵元素”）。

$a$ 到 $b$ 的弧线长度定义如下，其中参数定为 $t$ ， $t$ 由 $a$ 到 $b$ :

$\int_a^b \sqrt{ \sum_{ij}g_{ij}{dx^i\over dt}{dx^j\over dt}}dt$

两个切矢量的夹角 $\theta$ ,设矢量 $U=\sum_i u^i{\partial\over \partial x_i}$ 和 $V=\sum_i v^i{\partial\over \partial x_i}$ ，定义为：

$\cos \theta =\frac{\langle u, v\rangle}{|u||v|}= \frac{\sum_{ij}g_{ij}u^iv^j} {\sqrt{ \left| \sum_{ij}g_{ij}u^iu^j \right| \left| \sum_{ij}g_{ij}v^iv^j \right|}}$

a. 欧几里德几何度量

二维欧几里德度量张量：

$(g_{ij}) = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}$

其度规就是内积，而弧线长度的计算方式则可以转为我们熟悉的微积分方程计算方法：

$L=\int _{a}^{b}{\sqrt {\left({\frac {dx^{1}}{dt}}\right)^{2}+\left({\frac {dx^{2}}{dt}}\right)^{2}}}\mathrm {d} t$

这个计算方法可以由下图，将弧线切成一小段一小段来计算，很快得出。

下面介绍一些在其他坐标系统的欧氏度量：

b. 极坐标系： $(x^{1},x^{2})=(r,\theta )$

$(g_{ij}) = \begin{bmatrix} 1 & 0 \\ 0 & (x^1)^2\end{bmatrix}$

c. 圆柱坐标系： $(x^{1},x^{2},x^{3})=(r,\theta ,z)$

$(g_{ij}) = \begin{bmatrix} 1 & 0 & 0\\ 0 & (x^1)^2 & 0 \\ 0 & 0 & 1\end{bmatrix}$

d. 球坐标系： $(x^{1},x^{2},x^{3})=(r,\phi ,\theta)$

$(g_{ij}) = \begin{bmatrix} 1 & 0 & 0\\ 0 & (x^1)^2 & 0 \\ 0 & 0 & (x^1\sin x^2)^2\end{bmatrix}$

e. 平坦的闵可夫斯基空间 (狭义相对论)： $x^{0},x^{1},x^{2},x^{3})=(ct,x,y,z)$

$(g_{\mu\nu}) = (\eta_{\mu\nu}) \equiv \begin{bmatrix} -1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{bmatrix}$

在一些习惯中，与上面相反地，时间 $c t$ 的度规分量取正号而空间 $(x, y, z)$ 的度规分量取负号，故矩阵表示为：

$(g_{\mu\nu}) = (\eta_{\mu\nu}) \equiv \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1\end{bmatrix}$

2. 庞加莱圆盘模型（Poincaré disk model）

几何中，庞加莱圆盘模型，也叫共形圆盘模型，是一个 $n -$ 维双曲几何模型。几何中的点对应到 $n$ 维圆盘（或球）上的点，几何中的“直线”（准确地说是测地线）对应到任意垂直于圆盘边界的圆弧或是圆盘的直径。庞加莱圆盘模型、克莱因模型以及庞加莱半空间模型，一起被Eugenio Beltrami用来证明双曲几何与欧几里得几何的相容性等价。

1）引入

假设我们有这样⼀个双曲世界，整个世界限制在⼀个单位圆的范围内，这个世界有两条重要的物理定律:

假如某物体 $X$ 离原点 $O$ 距离为 $d$ ，那么该物体的温度为 $1-d^2$ ；
物体的大小与温度成正比。

那么就有如下的一些现象：

某个⼈从这个世界的中心走向边缘，那么他的温度会从 $1$ 慢慢变成 $0$ ，同时整个人慢慢变小。他自身大小改变的同时周围的物体也等比例地放大或缩小，因此他不会觉得自己变小了或者变大了；
对于我们来说，这个世界是有界的；但对于这个世界中的人来说，这个世界是无穷大的。因为离原点越远，人就越小，于是相对来说他们所看到的空间也就越大。当人的位置趋于边界时，物体大小趋于 $0$ ，此时的空间将变得无穷大，因此这个世界中的物体永远无法到达边界。

在这个世界中，需要重新定义距离：
$\frac{\Delta x}{1-d^{2}}$
也就是在原本的距离基础上，除以了 ${1-d^{2}}$ 。这就可以体现离原点越远，物体就越⼩，人的步子也越小，相对来说实际空间就变大了。而在下图中，从 $A$ 到 $B$ ，并不是直线最短，而是蓝色的曲线。

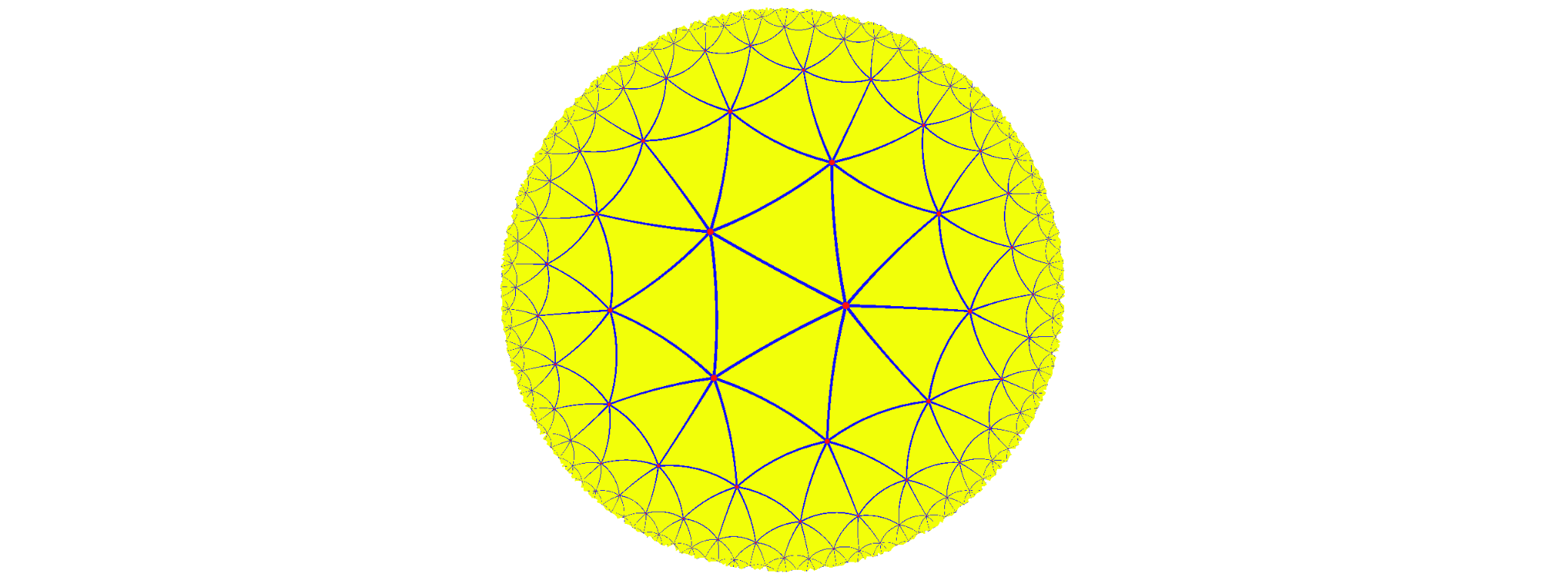
在这样一个世界中，我们眼中的直线，就是他们眼中曲线，并且过⼀点可以作无数条直线不与已知直线相交。这就是一个典型的庞加莱圆盘。下图为该平面上的一个三角形剖分，里面的所有三角形都是等边三角形，而且所有这些三角形都是一样大的。

下面对庞加莱圆盘里的度规进行标准定义：

在彭加莱圆盘上，对于任意点 $P (x, y)$ ，该点的任意两个向量为，则度规定义为：
$g(\textbf{u},\textbf{v})=\frac{2\textbf{u}\cdot \textbf{v}}{1-x^2-y^2}$
其中 $g$ 为 $P$ 点处的度规， $d(u,v)=\textbf{u}\cdot \textbf{v}$ 为欧氏空间下的两向量的内积。

同时我们也可以根据前面度规的定义，写出下面另一种形式：

$ds^2=\frac{4dx^2+4dy^2}{(1-x^2-y^2)^2}=\begin{pmatrix}dx&dy\end{pmatrix}\begin{pmatrix}\frac{4}{(1-x^2-y^2)^2}&0\\0&\frac{4}{(1-x^2-y^2)^2}\end{pmatrix}\begin{pmatrix}dx\\dy\end{pmatrix}$

或者极坐标的形式：

$ds^2=\frac{d\theta^2+r^2dr^2}{(1-r^2)^2}=\begin{pmatrix}d\theta&dr\end{pmatrix}\begin{pmatrix}\frac{1}{(1-r^2)^2}&0\\0&\frac{r^2}{(1-r^2)^2}\end{pmatrix}\begin{pmatrix}d\theta\\dr\end{pmatrix}$

双曲空间⼀个重要的特性是扩展的比欧氏空间快：当欧氏空间是多项式扩张的时候，双曲空间中是指数
型扩张，例如：双曲空间圆的长度和圆盘⾯积，都是指数扩张。

2）复杂网络中双曲几何

复杂网络背后的内蕴几何是双曲几何，体现在如下几点：

复杂网络连接一些可区分的异质的元素，这里的异质表明所有的节点可以以某种方式进行分类。一般情况下，这些分类表明，节点在分为一大组后还可以继续分为一些小的组。这些组和子组之间可以近似看为树结构，表示网络潜在的分层结构。而我们可以将树看作离散的双曲空间，双曲空间看作连续的树结构，从纯度量意义下，两者是相同的。
复杂网络的度幂律分布和聚类现象是双曲几何负曲率和度量性质的简单反映(例如，幂律度分布的指数是双曲空间曲率的函数)；
同样，如果⼀个复杂网络有幂律等性质，网络背后的内蕴几何是双曲几何。

由于几何框架有很强的异质性和聚类特性，而且高效鲁棒，因此非常适合用双曲几何来刻画复杂网络。下图刻画了树状结构与双曲空间的联系：

图刚开始形成的时候，是简并的，随着越来越多的节点加入，节点多元化且特殊化，因此加深了网络分类的层次性；
节点的一个特性表示为欧氏圆的一个点，所有特性表示为整个欧氏圆。不同节点之间欧氏圆越相近，表明越相似。

因此，如果假设节点属性首先具有某种度量结构，那么基于节点属性相似性的节点间距离可以映射到双曲空间中的距离。

3. 网络结构的双曲嵌入

下面我们回顾文本汇总最常用的嵌入模型——词嵌入（Word embedding），或词向量，其是自然语言处理（NLP）中语言模型与表征学习技术的统称。概念上而言，它是指把一个维数为所有词的数量的高维空间嵌入到一个维数低得多的连续向量空间中，每个单词或词组被映射为实数域上的向量。

词嵌入的方法包括人工神经网络等等，应用面最广的要属Word2vec。它有两种算法，分别是CBOW（Continuous Bagof-Words，给几个词，在这几个词出现的前提下来计算某个词出现的（事后）概率）、Skip-gram（根据某个词，然后分别计算它前后出现某几个词的各个概率）。这里我们以Skip-gram为例，网络结构如下所示：

输入层：当前单词的Onehot编码（单位向量）。假设单词向量空间维度为 $V$ ；
所有Onehot分别乘以共享的输入权重矩阵 $W$ ，其为 $\times N$ 矩阵， $N$ 为自己设定的数，初始化权重矩阵 $W$ ；
所得的向量相加求平均作为隐层向量，size为 $\times N$ ；
乘以输出 $\times V$ 的权重矩阵 $W^{'}$ ；
得到 $\times V$ 的向量，经激活函数处理得到 $V$ 维概率分布，概率最大的Index所指示的单词为预测出的中间词（target word），上下文单词个数共为 $C$ ；
所有 $C$ 个单词与真实标注的Onehot做比较，误差越小越好。

训练完毕后，输入层的每个单词与矩阵 $W$ 相乘得到的向量的就是词嵌入，这个矩阵（所有单词的词嵌入）也叫做look up table，其实就是矩阵 $W$ 自身，即任何一个单词的Onehot乘以这个矩阵都将得到自己的词向量。这里为了介绍简洁，Word2vec中的两种优化加速的方法：Hierarchical SoftMax 与 Negative Sampling 这里不再细述。

在上述的词嵌入例子中，损失函数为多元交叉熵损失：

$L(\Theta)=-\sum_{c=1}^{C}\log \frac{\exp \left(u_{c, j_{c}^{*}}\right)}{\sum_{j^{\prime}=1}^{V} \exp \left(u_{j^{\prime}}\right)}$

式子中的 $u$ 为内积，使得真实label与预测label相似时内积尽可能大，不相似时，内积尽可能小。但这个内积是定义在欧式空间上，而庞加莱嵌入的损失函数采用了类似的思想，但距离函数使用的是双曲距离，损失函数为（注意这里文章中应该写错了，需要加个负号）：

$L(\Theta)=-\sum_{(u, v) \in \mathscr{D}} \log \frac{e^{-d(\boldsymbol{u}, \boldsymbol{v})}}{\sum_{\boldsymbol{v}^{\prime} \in \mathcal{N}(u)} e^{-d\left(\boldsymbol{u}, \boldsymbol{v}^{\prime}\right)}}$

双曲距离我们定义为：

$d(\boldsymbol{u}, \boldsymbol{v})=\operatorname{arcosh}\left(1+2 \frac{\|\boldsymbol{u}-\boldsymbol{v}\|^{2}}{\left(1-\|\boldsymbol{u}\|^{2}\right)\left(1-\|\boldsymbol{v}\|^{2}\right)}\right)$

由于网络结构和树结构类似，这样定义可以包含层级结构的属性，同时还有以下特征：

距离平滑改变，这是能够找到分层连续嵌入的关键特性；
方程是对称的，空间的分层管理仅仅依赖于距离中心的距离，由于这种自控制性，可以用于无监督网络分层学习；
不仅可以学习分层结构，还可以学习相似性。

实际上使用的是庞加莱球, 而不是庞辦莱圆盘，这是由于：

很多数据有多个隐层级结构共存, 二维嵌入不太好表达；
高维嵌入降低优化难度。

由于庞加莱球具有黎曼流形结构，因此这里需要使用随机黎曼优化方法：

$\boldsymbol{\theta}_{t+1}=\boldsymbol{R}_{\theta_{t}}\left(-\eta_{t} \nabla_{R} \mathscr{L}\left(\boldsymbol{\theta}_{t}\right)\right)$

根据保角变换，将黎曼梯度下降转换为欧氏梯度下降。

最终可以根据该算法训练出的结果如下：

可以看到，训练完成后，哺乳动物的位置在最中心的根节点附近，而随着分支的不断细化，越往外的种类会越细，而且会有层级结构，如上图的比格犬就是在网络结构末梢。

4. 双曲嵌入神经网络

上面网络结构的双曲嵌入，虽然取得了不错的效果，但双曲空间的表征能力在很多方面不如欧氏空间，主要是缺少相应的神经网络层数。

2018年发表在NeurlIPS的Hyperbolic Neural Networks (HNN) 文章，通过将莫比乌斯陀螺向量空间的形式性与双曲空间的庞加莱模型的黎曼几何相结合，将深度学习推广到双曲空间。

1) 基本运算的重构

文章对基本运算进行重构，包括：加法运算、数乘运算、距离函数、指数对数变换、平移变换等：

a. Möbius addition

$\oplus_{c} y:=\frac{\left(1+2 c\langle x, y\rangle+c\|y\|^{2}\right) x+\left(1-c\|x\|^{2}\right) y}{1+2 c\langle x, y\rangle+c^{2}\|x\|^{2}\|y\|^{2}}.$

b. Möbius scalar multiplication

$\otimes_{c} x:=(1 / \sqrt{c}) \tanh \left(r \tanh ^{-1}(\sqrt{c}\|x\|)\right) \frac{x}{\|x\|}.$

c. Distance

$d_{c}(x, y)=(2 / \sqrt{c}) \tanh ^{-1}\left(\sqrt{c}\left\|-x \oplus_{c} y\right\|\right).$

d. Exponential and logarithmic maps

$\exp _{x}^{c}(v)=x \oplus_{c}\left(\tanh \left(\sqrt{c} \frac{\lambda_{x}^{c}\|v\|}{2}\right) \frac{v}{\sqrt{c}\|v\|}\right), \log _{x}^{c}(y)=\frac{2}{\sqrt{c} \lambda_{x}^{c}} \tanh ^{-1}\left(\sqrt{c}\left\|-x \oplus_{c} y\right\|\right) \frac{-x \oplus_{c} y}{\left\|-x \oplus_{c} y\right\|}.$

e. Parallel transport

$P_{\boldsymbol{0} \rightarrow x}^{c}(v)=\log _{x}^{c}\left(x \oplus_{c} \exp _{\boldsymbol{0}}^{c}(v)\right)=\frac{\lambda_{\boldsymbol{0}}^{c}}{\lambda_{x}^{c}} v.$

f. Geodesics （测地线，双曲空间中两点距离最短的线，相当于欧式空间的直线）

$\gamma_{x \rightarrow y}(t):=x \oplus_{c}\left(-x \oplus_{c} y\right) \otimes_{c} t, \quad \text { with } \gamma_{x \rightarrow y}: \mathbb{R} \rightarrow \mathbb{D}_{c}^{n} \text { s.t. } \gamma_{x \rightarrow y}(0)=x \text { and } \gamma_{x \rightarrow y}(1)=y.$

具体如下图的彩色线所示：

上面这些公式中的参数 $c$ 是相较于原本欧式空间的运算多出来的参数，它刻画了距离中心位置的远近程度，我们原本庞加莱圆盘的半径为 $1/\sqrt{c}$ 。当 $c = 0$ ，对应的公式退化到欧式空间中。

2) 空间转换

我们首先拿到的数据是双曲空间中的，我们需要通过将输入转换到欧式空间中，进行神经网络的学习与训练后，将输出结果再映射回双曲空间。而这种转换就是用我们前面定义的：log mapping 与 exp mapping。

log mapping 是将双曲空间变换到欧氏空间；
exp mapping 是将欧氏空间变换到双曲空间中。

整个的网络模型公式如下所示：

$f^{\otimes_{c}}(x):=\exp _{\boldsymbol{0}}^{c}\left(f\left(\log _{\boldsymbol{0}}^{c}(x)\right)\right)$

其中 $\exp _{\boldsymbol{0}}^{c}: T_{\boldsymbol{0}_{m}} \mathbb{D}_{c}^{m} \rightarrow \mathbb{D}_{c}^{m} \text { 以及 } \log_{\mathbf{0}}^{c}: \mathbb{D}_{c}^{n} \rightarrow T_{\mathbf{0}_{n}} \mathbb{D}_{c}^{n}$ 。 $f$ 则为我们欧式空间的神经网络。