目录

一.原码反码补码介绍（以8个比特位为例）

1.原码表示法

关于原码需要注意:

1.  符号位的0和1对应+和-，剩下的数值位就是真值的绝对值

2.  n个比特位的原码最大可以表示2^(n - 1) - 1,最小可以表示- (2^(n - 1) - 1)，例如2^8 = 256,则8个比特位的原码可以表示的范围为 -127 <= x <= 127

3.  在原码中，真值0的表示有两种，一种为正数0（0000 0000），一种为负数0（1000 0000）,不过表示的都是0

2.反码表示法

关于反码需要注意：

1.  反码中真值0也有2种表示方式:正数0（0000 0000）和负数0（1111 1111）

2.  反码的取值范围与相同位数的原码相同（以8比特位为例）

3.补码表示法

关于补码需要注意:

1.  补码的一个特性就是使得符号位也具有了权值，这使得补码之间可以直接进行运算，也可以通过计算直接将一个补码转换成十进制

2.  正数的原码，反码，补码都是相同的

3.  补码中0只有一种表示方法，为 0000 0000。而因为符号位也能直接参与运算，所以负数0（1000 0000）在补码中代表着-128。也正是因为这点，补码的取值范围变成了

4.  计算机中的负数一般使用补码表示，而补码的计算依赖于反码

补码的运算

1.  补码的加法

当进行补码相加时，我们可以按照普通的二进制加法规则进行操作，只是在最终结果中需要考虑溢出的情况

2.  补码的减法

两者相互转换的公式就是：全部位按位取反，再+1

---

复习知识:

无符号整数的表示：每一个比特位都参与运算

例如：无符号的25表示：0001  1001

1. 从右往左，第0位（最右边）的权重为2^0，第1位的权重为2^1，第2位的权重为2^2，依此类推（一共8位，全部都有权重并且都参与运算）。

2. 对每一位进行权重乘以该位的数值，然后将结果相加。

   (12^4 + 12^3 + 0*2^2 + 0*2^1 + 1*2^0)

   (= 16 + 8 + 0 + 0 + 1)

   (= 25)

无符号的147表示：1001 0011

(12^7 + 02^6 + 02^5 + 12^4 + 02^3 + 02^2 + 12^1 + 12^0)

(= 128 + 0 + 0 + 16 + 0 + 0 + 2 + 1)

(= 147)

一.原码反码补码介绍（以8个比特位为例）

无符号整数确实有用，但是现实生活中的计算通常是伴随着正负号，那么如何使用二进制表示数的正负呢?这时候就出现了原码

1.原码表示法

为了表示正负，原码规定：将最高的比特位设定为符号位，其他比特位设定为数值位，其中符号位的值为0表示正数，为1表示负数

例如：

1. 真值： 53 二进制：0011 0101        0表示这个数是正数
2. 真值：-53 二进制：1100 1011        1表示这个数是负数
3. 真值：-78 二进制：1011 0010

通过举例可以发现：数值位的值没有权重！！（即在将二进制转换成十进制的时候数值位不参与运算）

关于原码需要注意:

1.  符号位的0和1对应+和-，剩下的数值位就是真值的绝对值

2.  n个比特位的原码最大可以表示2^(n - 1) - 1,最小可以表示- (2^(n - 1) - 1)，例如2^8 = 256,则8个比特位的原码可以表示的范围为 -127 <= x <= 127

关于注意2的解释：8位的比特位，其中一位被占用变成了符号位，所以最大的正数就是 0111 1111

这个数换算成十进制就是127，负数就是符号位变成1，为1111 1111即-127。其他位数的同理

3.  在原码中，真值0的表示有两种，一种为正数0（0000 0000），一种为负数0（1000 0000）,不过表示的都是0

不知道大家有没有好奇过，编程语言中的一些基本类型为什么取值范围都不是对称的，以c语言中的有符号char(8bit)类型为例，它的取值范围是-128 ~ 127。造成这个原因就是因为0在原码中有2种表示方式，c语言的创作者觉得2个0用不上，浪费空间，所以将正数0（0000 0000）规定为0，而负数0（1000 0000）规定为-128，所以出现了-128 ~ 127。包括有符号int等其他基本类型都是这样

原码使用了一个比特位作为符号位，那么原码的缺点也很明显：负数和正数的表示方式不统一，符号位不能参与运算，加减法运算时需要分别处理负数和正数，导致计算过程复杂，例如

29          0001 1101                                         186

 +                   +                  = (按位相加)    101111010    

-29         1001 1101

这就导致了想要处理原码之间的运算，必须设计出更复杂的电路，这样一来会非常的烧脑烧钱

为了统一负数和正数的表示方式不统一的问题，同时解决在原码中，负数的相加可能会出现溢出的现象，反码孕育而生

2.反码表示法

反码是在原码的基础上，保持符号位不变，其他所有的符号位按位取反（原本是0就变成1，原本是1就变成0），并且正数的原码与反码相同

1. 十进制数：25
   二进制表示：0001 1001
   正数的反码：0001 1001（不变）

2. 十进制数：-42
   有符号二进制表示：1101 0110
   按位取反的二进制：1010 1001（符号位不变）

关于反码需要注意：

1.  反码中真值0也有2种表示方式:正数0（0000 0000）和负数0（1111 1111）

2.  反码的取值范围与相同位数的原码相同（以8比特位为例）

例如8个比特位的原码取值范围是-127  <= x <= 127，则反码取值范围也是-127  <= x <= 127

正数的原码与反码相同，所以反码的最大值就是原码的最大值为 0111 1111

反码的最小值就是原码最小的负数按位取反所得到的为 1000 0000 （1111 1111按位取反，符号位不变）

反码的一个主要用途是在计算机中表示负数，但是反码并不是现代计算机中最常用的表示负数的方法，而是为了解决早期计算机中的一些问题而提出的。

这个时候又发现，反码对于0的表示也有2种，这种表示方式不仅增加了运算的复杂度，还会导致算法的不一致性，那么为了统一0的表示方式，补码出现了

3.补码表示法

补码是在反码的基础上+1得来的，理由很简单，在反码中2个0的表示正数0（0000 0000）和负数0（1111 1111），+1即可让负数0消失，变成0。这样，真值0在补码中只有一种表示形式即 0000 0000

关于补码需要注意:

1.  补码的一个特性就是使得符号位也具有了权值，这使得补码之间可以直接进行运算，也可以通过计算直接将一个补码转换成十进制

2.  正数的原码，反码，补码都是相同的

3.  补码中0只有一种表示方法，为 0000 0000。而因为符号位也能直接参与运算，所以负数0（1000 0000）在补码中代表着-128。也正是因为这点，补码的取值范围变成了

- 2^(n - 1)  <=  2^(n - 1) - 1

-128这个值仅存在于补码中，它没有对应的原码和反码

4.  计算机中的负数一般使用补码表示，而补码的计算依赖于反码

当计算机将一个二进制数转换成补码后，就可以开始运算了

补码的运算

1.  补码的加法

当进行补码相加时，我们可以按照普通的二进制加法规则进行操作，只是在最终结果中需要考虑溢出的情况

计算 19 + (-20) 的补码相加：

首先，将 19 和 -20 的补码表示找出来：
- 19 的补码是 00010011
- -20 的补码是 11101100

然后进行二进制加法：

   00010011   (19)
+ 11101100   (-20)
   -------------
    11111111   (-1)
 

在8位有符号补码中，最高位是符号位，当溢出时，会导致结果不正确。在这种情况下，我们需要考虑溢出的情况，可能需要使用更多位来表示结果，或者在程序中进行适当的处理

因此，补码相加时，需要特别注意溢出的问题

2.  补码的减法

不论什么进制，加法和减法都是底层的电路来实现的。但是加法的电路设计比减法的电路要简单，并且造价更便宜，所以对于减法，通常是转成加法来进行计算

原理很简单  A - B = A + (- B)

这个公式要求我们将补码下的数B转换成 -B （再强调，这是仅限补码下的转换）

两者相互转换的公式就是：全部位按位取反，再+1

假设我们要将补码形式的数 -20 转换为正数形式。

首先，-20 的补码是 11101100。

按照补码转换规则，我们需要进行如下操作：

1. 全部位按位取反
2. 然后加1

首先，进行全部位按位取反：
11101100 取反得到 00010011

然后，加1：
00010011 + 1 = 00010100

因此，-20 的补码形式 11101100 转换为正数形式为 00010100，即 20

接下来直接和另一个数进行加法运算，将结果转成十进制就是正确答案了

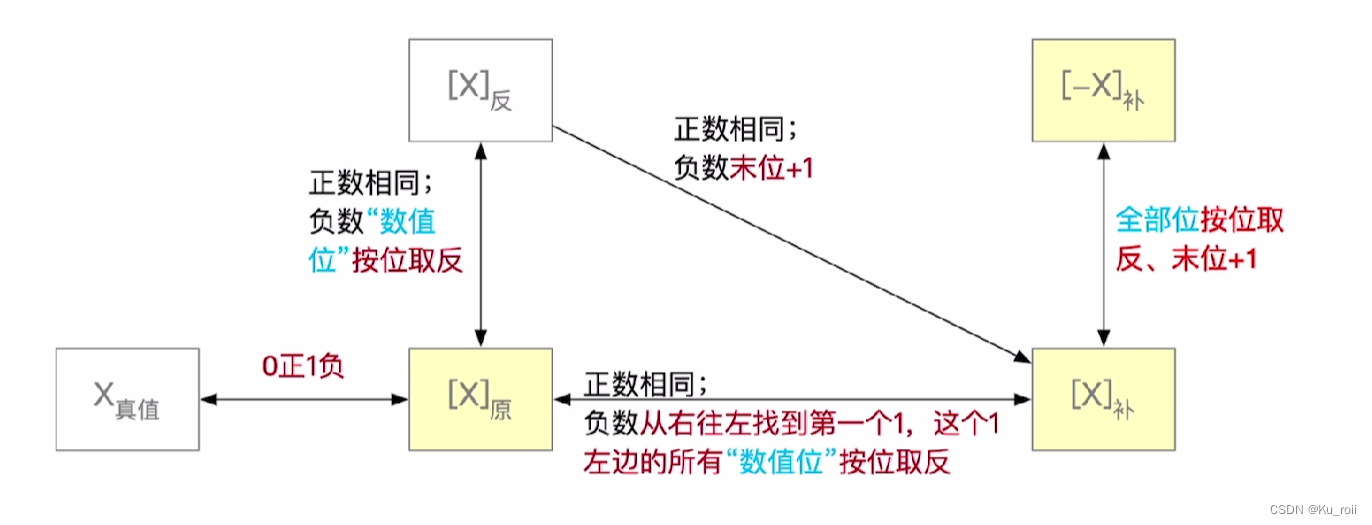
二.原码反码补码之间的关系