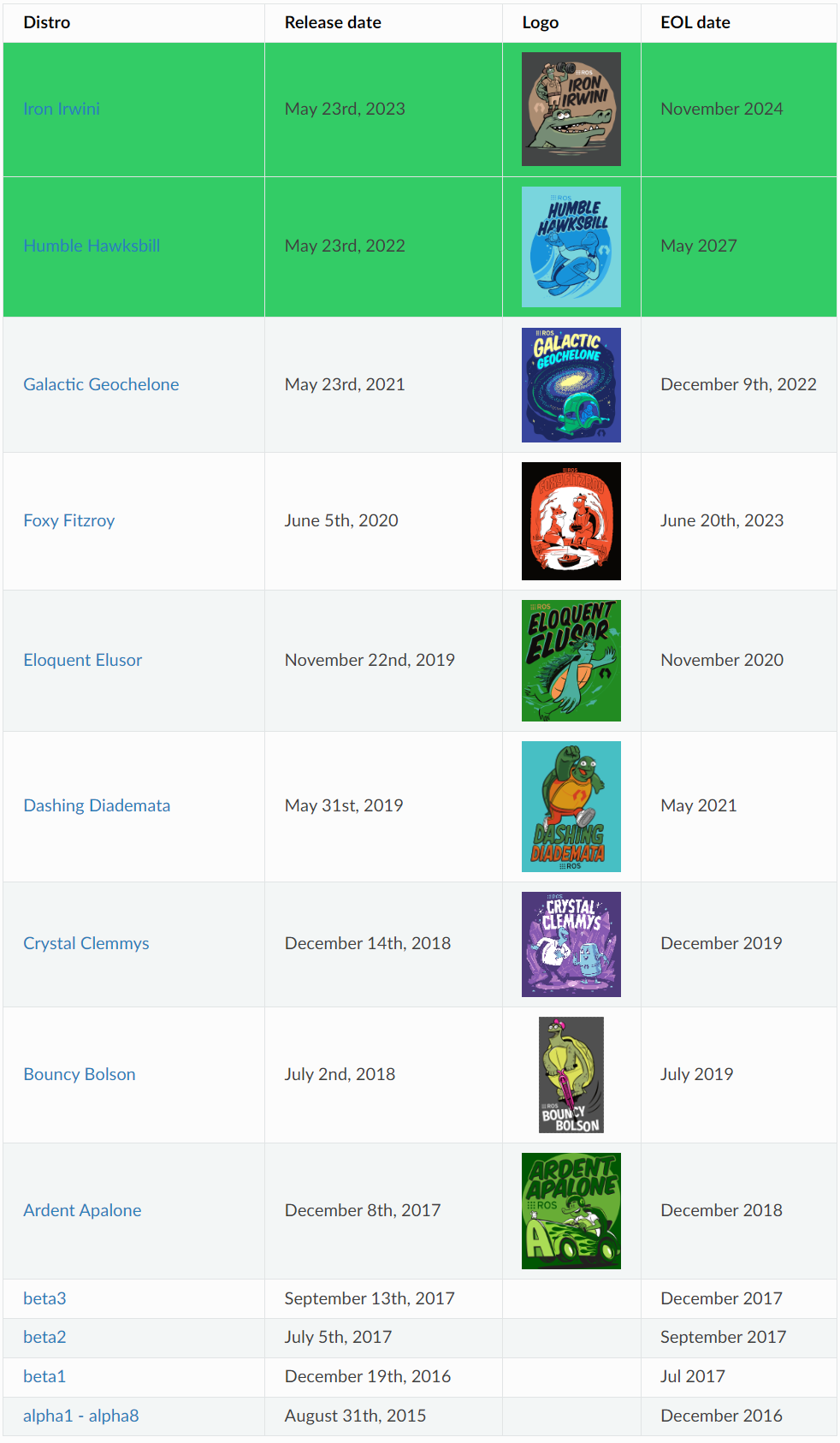
深入理解GELU激活函数：从原理到应用

在深度学习领域，激活函数的选择对模型的性能有着至关重要的影响。虽然ReLU（Rectified Linear Unit）因其简单高效而广受欢迎，但近年来，GELU（Gaussian Error Linear Unit）激活函数因其在特定场景下表现出的优异性能而逐渐受到关注。本文将详细介绍GELU激活函数的原理、特点以及应用，帮助读者全面理解这一激活函数的工作机制和使用场景。

什么是GELU激活函数？

GELU激活函数是由Dan Hendrycks和Kevin Gimpel在2016年提出的，它是一种基于高斯分布的非线性激活函数。GELU可以视为介于ReLU和Sigmoid/Tanh激活函数之间的折衷方案，它结合了ReLU的非饱和特性和Sigmoid/Tanh的平滑特性。

GELU的数学定义

GELU的数学表达式是：
$$\text{GELU}(x)=x\Phi (x)$$
其中，$\Phi (x)$ 是输入$x$的标准正态累积分布函数（CDF），具体公式为：
$$\Phi (x)=0.5\left(1+\text{erf}\left(\frac{x}{\sqrt{2}}\right)\right)$$
这里，$\text{erf}$是误差函数，用于计算$x$的高斯积分，这使得GELU具有平滑且非单调的性质。

GELU的特点与优势

平滑性

与ReLU的尖锐转折点不同，GELU提供了一个平滑的激活曲线，这有助于深度学习模型在训练过程中更加稳定，特别是在处理不连续输入数据时。

非饱和性

GELU与ReLU一样，具有非饱和性质，这意味着它可以缓解梯度消失问题，特别是在训练深层网络时。

自适应门控机制

GELU通过其内部的高斯CDF组件，实现了一种自适应的门控机制。这意味着GELU可以根据输入的属性自动调整激活的量，类似于神经元的开/关切换，这有助于网络自动学习重要的特征。

GELU在实际应用中的表现

GELU激活函数已经被广泛应用于多种先进的神经网络架构中，特别是在自然语言处理（NLP）模型如Transformer和BERT中。这些模型表明，GELU可以在处理复杂和高维数据时，提供比传统激活函数更好的性能和泛化能力。

结论

GELU激活函数是深度学习模型中的一个强大工具，它结合了ReLU和Sigmoid的优点，提供了一种高效且稳定的方式来增强模型的学习能力。无论是在视觉还是在文本相关的任务中，GELU都显示出了其独特的优势，值得更多研究者和工程师的关注和实验。