熵权法（Entropy Weight Method，简称 EWM）是一种用于确定多指标评价体系中各个指标权重的方法。在多属性决策分析中，不同指标对总体评价结果的影响程度不同，因此需要设定权重。熵权法的核心思想是根据信息熵的大小来衡量各个指标的信息量，并以此来确定指标的重要性。熵值越小，说明信息量越大，权重也应该越高。这种方法能够很好地避免主观因素的干扰，使得权重的确定更加科学和客观。

一、信息熵的基本概念

熵这个概念源自物理学和信息论。在信息论中，熵（Entropy）用来衡量一个系统的不确定性程度。在决策分析中，如果一个指标的数据差异很大，意味着它提供了大量的信息；相反，如果数据差异很小，则说明它提供的信息量很少。

举个例子，假设我们在比较几款笔记本电脑的价格。如果每款电脑的价格都非常接近，那就意味着“价格”这一指标并没有为我们提供有用的信息，价格的分布是“有序”的、不确定性低的，其熵值会较高；但如果价格有很大的差异，这样的分布更“无序”，它的熵值就会较低，说明价格的信息量大，可以在决策中占据较大的权重。

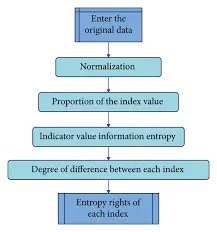
二、熵权法的计算步骤

熵权法的具体计算过程可以分为以下几步，包括数据标准化、计算信息熵、计算熵权等。我们通过一个具体的例子来演示熵权法的应用。

假设有四个不同的城市（A、B、C、D），需要对这些城市的宜居程度进行评估。我们选择了三个指标来进行评估：空气质量（AQI）、平均房价、绿化覆盖率。各城市的具体数据如下：

城市	空气质量 (AQI)	平均房价 (万元)	绿化覆盖率 (%)
A	70	15	30
B	50	18	40
C	90	20	50
D	60	17	45

我们需要使用熵权法来为这三个指标确定权重。

1. 数据标准化处理

由于各指标的量纲不同（例如 AQI 和房价），需要对原始数据进行标准化处理。标准化的目的是将不同单位的数据转换到同一范围，以便后续的熵值计算。

标准化公式有多种形式，这里选择向量归一化的形式：

[
X’{ij} = \frac{X{ij}}{\sqrt{\sum_{i=1}^n X_{ij}^2}}
]

对于空气质量指标，计算标准化值：

• 城市 A 的空气质量标准化值为：( X’_{A, AQI} = \frac{70}{\sqrt{70^2 + 50^2 + 90^2 + 60^2}} = \frac{70}{126.49} = 0.553 )
• 城市 B 的空气质量标准化值为：( X’_{B, AQI} = \frac{50}{126.49} = 0.395 )
• 城市 C 的空气质量标准化值为：( X’_{C, AQI} = \frac{90}{126.49} = 0.712 )
• 城市 D 的空气质量标准化值为：( X’_{D, AQI} = \frac{60}{126.49} = 0.474 )

类似地，可以计算其他指标的数据标准化值。

2. 计算每个指标的信息熵

信息熵的计算公式为：

[
H_j = -k \sum_{i=1}^n f_{ij} \ln(f_{ij})
]

其中 ( f_{ij} ) 表示第 ( i ) 个样本在第 ( j ) 个指标上的占比，( k = \frac{1}{\ln(n)} )，( n ) 是样本的个数。为了避免对数计算时出现无穷大的情况，通常对 ( f_{ij} ) 加上一个很小的正数（例如 ( \epsilon = 10^{-10} )）。

根据标准化后的值计算每个城市在某个指标上的占比，例如，空气质量指标下城市 A 的占比为：

[
f_{A, AQI} = \frac{X’{A, AQI}}{\sum{i=1}^n X’_{i, AQI}} = \frac{0.553}{0.553 + 0.395 + 0.712 + 0.474} = 0.271
]

类似地，计算其他城市在空气质量指标上的占比。接着，根据熵的公式计算空气质量指标的信息熵。

3. 计算权重

信息熵计算完成后，可以得到每个指标的权重。权重的公式为：

[
w_j = \frac{1 - H_j}{\sum_{j=1}^m (1 - H_j)}
]

其中 ( H_j ) 为第 ( j ) 个指标的信息熵，( m ) 是指标的总数。

如果某个指标的信息熵较小，意味着它对总体的不确定性贡献较大，也就是说它包含更多有用的信息，因此其权重也会更高。

三、熵权法的优势与局限性

熵权法的主要优势在于它能够通过客观的数据分析，自动计算各个指标的权重，避免了人为干扰导致的偏差。通过引入信息论中的熵的概念，熵权法能够有效地衡量各指标对决策的重要性。

以环境质量评估为例，如果我们需要评估多个城市的宜居程度，除了空气质量、房价等指标外，还可以加入其他维度的信息，如医疗资源、公共交通便利程度等。熵权法在这种多维度的场景下，能够动态地根据指标的数据分布情况调整权重，使得每个指标的影响力更加合理。

不过，熵权法也存在一些局限性。例如，它完全依赖于数据的客观性，无法反映专家的主观偏好。如果数据存在噪声或者不准确，最终得到的权重也会受到影响。此外，熵权法对数据的要求较高，需要数据具有足够的差异性，否则熵值计算的结果可能会导致某些指标的权重过低或过高。

四、真实案例：城市宜居度评估

为了使熵权法的应用更为具体，这里以城市宜居度评估为例，进一步说明其实际应用。

假设某环保组织希望评估五个城市的宜居程度，并根据结果给出改善建议。选取的指标包括空气质量、住房价格、公共交通的便利性和医疗设施的覆盖率。通过熵权法，我们首先对每个城市在这些指标上的表现进行数据收集，并进行标准化处理。然后，使用熵值计算每个指标的信息量，最终确定各指标的权重。

结果发现，空气质量和公共交通的权重较高，这意味着这两个因素对城市宜居度的影响更大。因此，环保组织可以建议各城市优先改善空气质量，增加公共交通投入，从而提高整体的宜居水平。

这个案例清楚地表明了熵权法在复杂决策中的应用价值，尤其是在涉及多维度和多指标的评价体系中。通过科学地确定权重，决策者能够更准确地把握重点，进行资源分配和优化改进。

五、太长不看版

熵权法是一种基于数据分布特征的客观赋权方法，在多属性决策分析中具有广泛的应用。它通过衡量各指标的信息熵，来确定其在整体决策中的重要性，这使得熵权法特别适用于需要客观赋权的场景。

然而，熵权法的应用效果也取决于数据的质量和维度的选择。在未来的研究中，可以将熵权法与其他赋权方法结合，如 AHP（层次分析法）或主成分分析法，以更好地解决复杂的决策问题。通过融合主观和客观的信息，决策者可以在数据驱动和专家经验之间取得平衡，从而做出更加科学合理的决策。

在应用层面，随着大数据和人工智能技术的发展，熵权法在多领域的应用也越来越广泛。例如，在智能制造中，可以使用熵权法来评价生产线的各项性能指标，从而优化生产效率；在金融风险评估中，也可以通过熵权法确定不同风险因子的权重，从而提高评估的精度。这些都是熵权法在现代技术背景下的潜在应用方向。