FaceChain团队NeurIPS 2024新作TopoFR,拓扑对齐的人脸表征模型
当前人脸识别研究集中于设计高效的基于Margin损失函数和复杂的网络架构,以提升卷积神经网络捕捉人脸细节特征的能力。无监督学习和图神经网络的成功显示了数据结构对模型泛化能力的重要性。尽管大规模人脸识别数据集包含丰富的结构信息,但目前尚无研究探讨如何利用这些信息提升模型在实际场景中的泛化性能。本文提出TopoFR,将大规模人脸数据集中的内在结构信息融入隐层空间,以显著提高人脸识别模型在真实环境中的泛
FaceChain团队NeurIPS 2024新作TopoFR,拓扑对齐的人脸表征模型
一、前言
在数字人领域,形象的生成需要依赖于基础的表征学习。FaceChain团队除了在数字人生成领域持续贡献之外,在基础的人脸表征学习领域也一直在做深耕。采用了新一代的Transformer人脸表征模型TransFace后,FaceChain去年也是推出了10s直接推理的人物写真极速生成工作,FaceChain-FACT。继TransFace之后,FaceChain团队最近被机器学习顶级国际会议NeurIPS 2024接收了一篇人脸表征学习新作, “TopoFR: A Closer Look at Topology Alignment on Face Recognition”,让我们来一睹为快。
**(i)**论文链接:http://arxiv.org/abs/2410.10587
**(ii)**开源代码:https://github.com/modelscope/facechain/tree/main/face_module/TopoFR
二、背景
1. 人脸识别
卷积神经网络在自动提取人脸特征并用于人脸识别任务上已经取得了巨大的成功。训练基于卷积神经网络的人脸识别模型的损失函数主要分为以下两种类型:(1)基于Metric的损失函数, 例如 Triplet loss, Tuplet loss 以及 Center loss. (2) 基于Margin的损失函数, 例如 ArcFace, CosFace, CurricularFace 与 AdaFace.
相比于基于Metric的损失函数, 基于Margin的损失函数能够鼓励模型执行更加高效的样本到类别的比较,因此能够促进人脸识别模型取得更好的识别精度。其中,ArcFace成为业界训练人脸识别模型首选的损失函数。
2. 持续同调
下面介绍一下持续同调与我们方法相关的一些知识。
持续同调是一种计算拓扑学方法,它致力于捕捉Vietoris-Rips复形随着尺度参数 ρ \rho ρ变化而进化的过程中所呈现的拓扑不变性特征,其主要用于分析复杂点云的潜在拓扑结构。近年来,持续同调技术在信号处理、视频分析、神经科学、疾病诊断以及表征学习策略评估等领域表现出了极大的优势。在机器学习领域,一些研究已经证明了在神经网络训练过程中融入样本的拓扑特征可以有效地提高模型的性能。
符号: X : = { x i } i = 1 n \mathcal{X}:=\left \{x_{i} \right \}_{i=1}^{n} X:={xi}i=1n表示一个点云, μ \mu μ表示一个在 X \mathcal{X} X空间中的距离度量。矩阵 M \mathcal{M} M表示点云 X \mathcal{X} X中各点之间的成对距离矩阵。
**Vietoris-Rips复形:**Vietoris-Rips 复形是从度量空间中一组点构建的特殊单纯复形,可用于近似表示底层空间的拓扑结构。对于 0 ≤ ρ < ∞ 0\leq \rho < \infty 0≤ρ<∞,我们表示点云 X \mathcal{X} X在尺度 ρ \rho ρ处所对应的Vietoris-Rips复形为 V ρ ( X ) \mathcal{V}{\rho}(\mathcal{X}) Vρ(X), 其包含了点云 X \mathcal{X} X中所有的单纯形(即子集),并且点云 X \mathcal{X} X中的每个成分满足一个的距离约束: ∀ i , j \forall i,j ∀i,j, μ ( x i , x j ) ≤ ρ \mu(x_{i},x_{j})\leq \rho μ(xi,xj)≤ρ。
此外Vietoris-Rips 复形还满足一个嵌套关系: ∀ ρ i ≤ ρ j \forall \rho_{i}\leq\rho_{j} ∀ρi≤ρj, V ρ i ⊆ V ρ j \mathcal{V}_{\rho_{i}}\subseteq \mathcal{V}_{\rho_{j}} Vρi⊆Vρj。基于这个关系,我们能够随着尺度系数 ρ \rho ρ的增加而追踪单纯复形的进化过程。 值得注意的是 V ρ ( X ) \mathcal{V}{\rho}(\mathcal{X}) Vρ(X)和 V ρ ( M ) \mathcal{V}{\rho}(\mathcal{M}) Vρ(M)是等价的,因为构建 Vietoris-Rips 复形只需要距离信息。
同调群: 同调群是一种代数结构,用于分析不同维度 j j j下单纯复形的拓扑特征,例如连通分量 ( H 0 H_{0} H0)、环 ( H 1 H_{1} H1)、空洞 ( H 2 H_{2} H2) 和更高维特征 ( H j , j ≥ 3 H_{j}, j\geq3 Hj,j≥3)。通过跟踪 Vietoris-Rips 复形的拓扑特征 H j H_{j } Hj随着尺度 ρ \rho ρ增加而呈现的相应变化,可以深入了解底层空间的多尺度拓扑信息。
**持续图和持续配对:**持续图
D
\mathcal{D}
D是笛卡尔平面
R
2
\mathcal{R}^{2}
R2中点
(
b
,
d
)
(b,d)
(b,d)的多重集合,其编码了关于拓扑特征寿命的信息。具体来说,它总结了每个拓扑特征的诞生时间
b
b
b和消失时间
d
d
d,其中诞生时间
b
b
b表示特征被创建的尺度,而消失时间$d
指的是特征被销毁的尺度。持续配对
指的是特征被销毁的尺度。持续配对
指的是特征被销毁的尺度。持续配对\gamma
包含与持久图
包含与持久图
包含与持久图\mathcal{D}
中标识的拓扑特征的诞生和消失相对应的单纯形
中标识的拓扑特征的诞生和消失相对应的单纯形
中标识的拓扑特征的诞生和消失相对应的单纯形r_{i}, r_{j}\in \mathcal{V}_{\rho}(\mathcal{X})
的索引
的索引
的索引(i,j)$。
三、方法
1. 本文动机
现存的人脸识别工作主要关注于设计更高效的基于Margin的损失函数或者更复杂的网络架构, 以此来帮助卷积神经网络更好地捕捉细腻度的人脸特征.
近年来,无监督学习和图神经网络的成功已经表明了数据结构在提升模型泛化能力中的重要性。大规模人脸识别数据集中天然地蕴含着丰富的数据结构信息,然而,在人脸识别任务中,目前还没有研究探索过如何挖掘并利用大规模数据集中所蕴含的结构信息来提升人脸识别模型在真实场景中的泛化性能。因此本文致力于将大规模人脸数据集中内在的结构信息注入进隐层空间中,以此来显著提升人脸识别模型在真实场景中的泛化性能。
我们使用持续同调技术调研了现存的基于卷积神经网络的人脸识别模型框架数据结构信息的变化趋势,如图1与图2所示,并得到了以下三个新颖观测结论:
**(i)**随着数据量的增大,输入空间的拓扑结构变得越来越复杂
**(ii)**随着数据量的增大,输入空间与隐层空间的拓扑结构差异越来越大
**(iii)**随着网络深度的增加,输入空间与隐层空间的拓扑结构差异越来越小,这也揭示了为什么越深的神经网络能够达到越高的人脸识别精度。

**图1:**我们分别从 MS1MV2 数据集中抽样了 1000(a)、5000(b)、10000(c)和 100000(d)张人脸图像,并使用持续同调技术计算它们的持续图,其中 H j H_{j} Hj表示第 j j j维同调。持续图是用来描述空间拓扑结构的数学工具,其中持久图中的第 j j j维同调 H j H_{j} Hj代表空间中的第 j j j维空洞。在拓扑理论中,如果空间中高维空洞的数量越多,那么底层空间的拓扑结构就更越复杂。如图 1(a)-1(d) 所示,随着人脸数据量的增加,输入空间的持久图中包含的高维空洞(如 H 3 H_{3} H3和 H 4 H_{4} H4)也越来越多。因此,这一实验现象清晰地表明了输入空间的拓扑结构也变得越来越复杂。
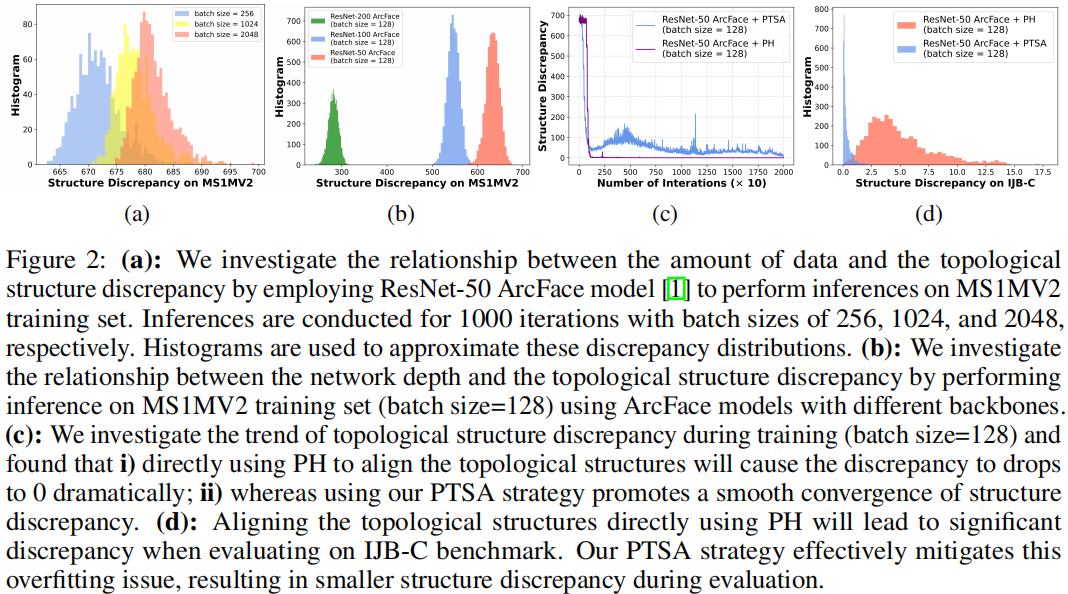
图2:(a) 我们首先使用基于ResNet-50架构的ArcFace 模型对 MS1MV2 训练集执行推断,以此来探究数据量与拓扑结构差异之间的关系。在推断时,batch-size被分别设置为 256、1024 和 2048,并分别进行了 1000 次迭代。我们使用直方图来近似这些拓扑结构差异分布。(b) 其次,我们使用具有不同ResNet架构的 ArcFace 模型在 MS1MV2 训练集上进行推断(batch-size=128)以此来研究网络深度与拓扑结构差异之间的关系。(c) 此外,我们研究了训练过程中拓扑结构差异的变化趋势(批量大小=128),发现 i) 直接使用 PH 对齐拓扑结构会导致差异急剧减少至 0,这意味着隐层空间的拓扑结构遭遇了结构崩塌现象;**ii) 而我们的 PTSA 策略促进了结构差异的平稳收敛,有效地将输入空间的结构信息注入进隐层空间。(d) **直接使用 PH 对齐拓扑结构会导致模型在 IJB-C 测试集中出现显著差异。我们的 PTSA 策略有效缓解了这种过拟合问题,在IJB-C数据集上评估过程中展现出更小的拓扑结构差异。
基于以上的观测结论,我们可以推断出,在大规模识别数据集上训练人脸识别模型时,人脸数据的结构信息将被严重破坏,这无疑限制了人脸识别模型在真实应用场景中的泛化能力。
因此,本文研究的问题是,在人脸识别模型训练过程中,如何在隐层空间有效地保留输入空间的数据所蕴含的结构信息,以此提升人脸识别模型在真实场景中的泛化性能。
2. 具体策略
2.1 模型的整体架构
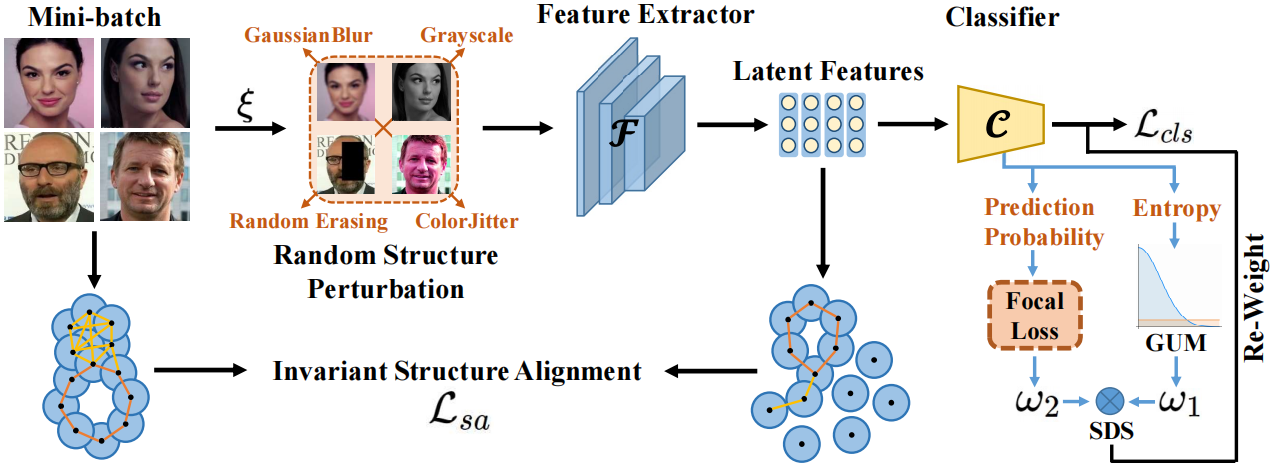
针对上述问题,本文从计算拓扑学角度出发,提出了基于拓扑结构对齐的人脸识别新框架TopoFR,如下图3所示。

**图3:**所提出的TopoFR模型整体架构示意图。 ⨂ \bigotimes ⨂表示乘法操作。 ξ \xi ξ表示对每个训练样本应用 RSP 的概率。
2.2 扰动引导的拓扑结构对齐策略 PTSA
我们发现,直接采用持续同调技术对齐人脸识别模型输入空间和隐层空间的拓扑结构,难以在隐层空间上本质保留输入空间的结构信息,进而容易导致模型的隐层空间遭遇结构崩塌现象. 为了解决这个问题,我们提出了扰动引导的拓扑结构对齐策略 PTSA,其包含了两个机制: 随机结构扰动 RSP 和 不变性结构对齐 ISA。
【随机结构扰动 RSP】
RSP 引入了一个多样性数据增强集合 A = { A 1 , A 2 , A 3 , A 4 } \mathcal{A}=\left \{\mathcal{A}_{1},\mathcal{A}_{2},\mathcal{A}_{3},\mathcal{A}_{4}\right \} A={A1,A2,A3,A4},其中包含了四个常见的数据增强运算: 随机擦除 A 1 \mathcal{A}_{1} A1,高斯模糊 A 2 \mathcal{A}_{2} A2,灰度化 A 3 \mathcal{A}_{3} A3以及颜色增强 A 4 \mathcal{A}_{4} A4。对于每一个训练样本 x i x_{i} xi,RSP会随机挑选一个数据增强 A r \mathcal{A}_{r} Ar运算来对其进行扰动:
x ~ i = A r ( x i ) \widetilde{x}_{i}=\mathcal{A}_{r}(x_{i}) x i=Ar(xi)
其次,扰动后的样本 x ~ i \widetilde{x}_{i} x i将正式送入网络进行有监督训练,这极大地增加隐层特征空间的拓扑结构多样性。我们采用ArcFace Loss作为基础分类损失函数:
L a r c ( x ~ i , y i ) = − log e s ( cos ( θ i y + m ) ) e s ( cos ( θ i y + m ) ) + ∑ k = 1 , k ≠ y K e s cos θ i k \mathcal{L}_{arc}(\widetilde{x}_{i},y_{i})=-\log\frac{e^{s(\cos(\theta^{y}_{i}+m))}}{e^{s(\cos(\theta^{y}_{i}+m))}+\sum_{k=1,k\neq y}^{K}e^{s\cos\theta^{k}_{i}}} Larc(x i,yi)=−loges(cos(θiy+m))+∑k=1,k=yKescosθikes(cos(θiy+m))
【不变性结构对齐 ISA】
在网络训练过程中,我们分别构建出原始输入空间 X \mathcal{X} X与扰动特征空间 Z ~ \widetilde{\mathcal{Z}} Z 的Vietoris-Rips 复形 V ρ ( X ) \mathcal{V}_{\rho}(\mathcal{X}) Vρ(X)和 V ρ ( Z ~ ) \mathcal{V}_{\rho}(\widetilde{\mathcal{Z}}) Vρ(Z )。 并利用持续同调技术求解出其对应的持续图 { D X , D Z ~ } \left \{\mathcal{D}^{\mathcal{X}},\mathcal{D}^{\widetilde{\mathcal{Z}}}\right \} {DX,DZ }和 持续配对 { γ X , γ Z ~ } \left \{\gamma^{\mathcal{X}},\gamma^{\widetilde{\mathcal{Z}}}\right \} {γX,γZ }。理想地,不管输入的人脸图像怎样被干扰,其编码在隐层空间中的位置应该保持不变。因此,我们提出对齐原始输入空间和扰动特征空间的拓扑结构,不变性结构对齐机制所对应的损失函数如下所示:
L s a ( D X , D Z ~ ) = 1 2 ( ∥ M X [ γ X ] − M Z ~ [ γ X ] ∥ 2 + ∥ M Z ~ [ γ Z ~ ] − M X [ γ Z ~ ] ∥ 2 ) \mathcal{L}_{sa}(\mathcal{D}^{\mathcal{X}},\mathcal{D}^{\widetilde{\mathcal{Z}}}) = \frac{1}{2} \left ( \left \| \mathcal{M}^{\mathcal{X}}[\gamma^{\mathcal{X}}]- \mathcal{M}^{\widetilde{\mathcal{Z}}}[\gamma^{\mathcal{X}}] \right \|^{2} + \left \| \mathcal{M}^{\widetilde{\mathcal{Z}}}[\gamma^{\widetilde{\mathcal{Z}}}]- \mathcal{M}^{\mathcal{X}}[\gamma^{\widetilde{\mathcal{Z}}}] \right \|^{2}\right ) Lsa(DX,DZ )=21( MX[γX]−MZ [γX] 2+ MZ [γZ ]−MX[γZ ] 2)
2.3 结构破坏性估计 SDE
在实际的人脸识别场景中,训练集通过会包含一些低质量的人脸图像,这也被称为困难样本。这些困难样本在隐层空间中很容易被编码到靠近决策边界附近的异常位置,严重破坏了隐层空间的拓扑结构,并会影响输入空间和隐层空间拓扑结构的对齐。
为了解决这个问题,我们提出了结构破坏性估计策略 **SDE **来精准地识别出这些困难样本,并鼓励模型在训练阶段重点学习这些样本,逐渐引导起回归到合理的空间位置上。
【预测不确定性】
困难样本通常分布在决策边界附近,因此也有着较大的预测不确定性 (即分类器处的预测分布熵较大) ,这也是其容易被错误分类的原因。为精准地筛选出这些困难样本, 我们提出利用高斯-均匀混合分布概率模型来建模这些样本的预测不确定性,其利用分类器处的预测熵作为概率分布的变量:
p ( E ( g ~ i ) ∣ x ~ i ) = π N + ( E ( g ~ i ) ∣ 0 , Σ ) + ( 1 − π ) U ( 0 , Ω ) p\left ( E(\widetilde{g}_{i})|\widetilde{x}_{i} \right )=\pi \mathcal{N}^{+}(E(\widetilde{g}_{i})|0,\Sigma)+(1-\pi)\mathcal{U}(0,\Omega) p(E(g i)∣x i)=πN+(E(g i)∣0,Σ)+(1−π)U(0,Ω)
其中,均匀分布 U ( 0 , Ω ) \mathcal{U}(0,\Omega) U(0,Ω)建模了困难样本,而高斯分布 N + ( E ( g ~ i ) ∣ 0 , Σ ) \mathcal{N}^{+}(E(\widetilde{g}_{i})|0,\Sigma) N+(E(g i)∣0,Σ)建模了简单样本。 因此,某个样本属于困难样本(即由于较大的预测不确定性)的后验概率可以被计算为:
h φ ( x ~ i ) = P φ ( u i = 1 ∣ x ~ i ) = ( 1 − π ) U ( 0 , Ω ) π N + ( E ( g ~ i ) ∣ 0 , Σ ) + ( 1 − π ) U ( 0 , Ω ) h_{\varphi}(\widetilde{x}_{i}) = P_{\varphi} \left ( u_{i}=1 | \widetilde{x}_{i} \right ) = \frac{(1-\pi)\mathcal{U}(0,\Omega )}{\pi \mathcal{N}^{+}(E(\widetilde{g}_{i})|0,\Sigma)+ (1-\pi)\mathcal{U}(0,\Omega )} hφ(x i)=Pφ(ui=1∣x i)=πN+(E(g i)∣0,Σ)+(1−π)U(0,Ω)(1−π)U(0,Ω)
当分类器的预测分布十分接近于均匀分布时,那么样本属于困难样本的概率将十分接近于1。
【结构破坏性分数 SDS】
相比于正确分类样本,错误分类样本有着更大的困难性,并且对隐层空间的拓扑结构损害更大。受Focal Loss设计思想的启发,我们在衡量样本对空间结构破坏性大小时综合考虑了预测不确定性与预测精度,并设计出概率感知的打分机制 ω ( x ~ i ) \omega(\widetilde{x}_{i}) ω(x i)来自适应地为每个样本计算结构破坏性分数 SDS:
ω ( x ~ i ) = ω 1 ( x ~ i ) × ω 2 ( x ~ i ) = ( 1 + h φ ( x ~ i ) ) λ × ( 1 − g ~ i g t ) \omega(\widetilde{x}_{i})=\omega_{1}(\widetilde{x}_{i})\times\omega_{2}(\widetilde{x}_{i})=(1+h_{\varphi}(\widetilde{x}_{i}))^{\lambda}\times(1-\widetilde{g}_{i}^{gt}) ω(x i)=ω1(x i)×ω2(x i)=(1+hφ(x i))λ×(1−g igt)
为鼓励模型在训练阶段重点关注那些对拓扑结构破坏较大的困难样本, 我们将结构破坏性分数SDS加权至最终的分类损失函数上:
L c l s = ω ( x ~ i ) × L a r c ( x ~ i , y i ) \mathcal{L}_{cls}=\omega(\widetilde{x}_{i})\times \mathcal{L}_{arc}(\widetilde{x}_{i},y_{i}) Lcls=ω(x i)×Larc(x i,yi)
在训练过程中,最小化 L c l s \mathcal{L}_{cls} Lcls将带来两个好处:
**(i)**最小化
L
a
r
c
\mathcal{L}_{arc}
Larc将鼓励模型从多样化的训练样本中捕捉出更有泛化性的人脸特征。
**(ii)**最小化结构破坏性分数SDS
ω
(
⋅
)
\omega(\cdot)
ω(⋅)能够有效减轻困难样本对隐层空间结构的破坏,这有利于结构信息的保留以及清晰决策边界的构建。
2.4 模型优化
TopoFR模型整体的目标函数如下所示:
min F , C L c l s + α L s a \min\limits_{\mathcal{F},\mathcal{C}}\mathcal{L}_{cls}+ \alpha \mathcal{L}_{sa} F,CminLcls+αLsa
四、关键实验及分析
1.1 训练数据集与测试基准
我们分别采用MS1MV2 (5.8M 图像, 85K 类别),**Glint360K **(17M 图像, 360K 类别) 以及 WebFace42M (42.5M 图像, 2M 类别) 作为我们模型的训练集。
利用 **LFW, AgeDB-30, CFP-FP, IJB-C 以及 IJB-B **等多个人脸识别测试基准来评估我们模型的识别与泛化性能。
1.2 在 LFW, CFP-FP, AgeDB-30, IJB-C 以及 IJB-B 测试基准上的实验结果
我们可以观察到,TopoFR在这些简单的基准上的性能几乎达到了饱和,并显著高于对比方法。此外,TopoFR在不同ResNet框架下都取得了SOTA性能。值得一提的是,我们基于ResNet-50架构的TopoFR模型甚至超越了大部分基于ResNet-100的竞争者模型。

1.3 **高斯-均匀混合分布概率模型**的有效性
为验证高斯-均匀混合分布概率模型在挖掘困难样本方面的有效性,我们展示了模型训练过程中利用分类器预测熵所估计的高斯分布密度函数,如下图4所示。
结果表明,被错误分类的困难样本通常有着较小的高斯密度(即有着较高的高斯-均匀混合分布后验概率),因此能够被高斯-均匀混合分布概率模型轻易探测出来。提得一提的是,即使部分被错误分类的困难样本有着较小的熵(即有着较大的高斯密度和较低的后验概率),它们的结构性破坏分数 ω ( ⋅ ) \omega(\cdot) ω(⋅)也能被Focal Loss ω 2 ( ⋅ ) \omega_{2}(\cdot) ω2(⋅)所修正。
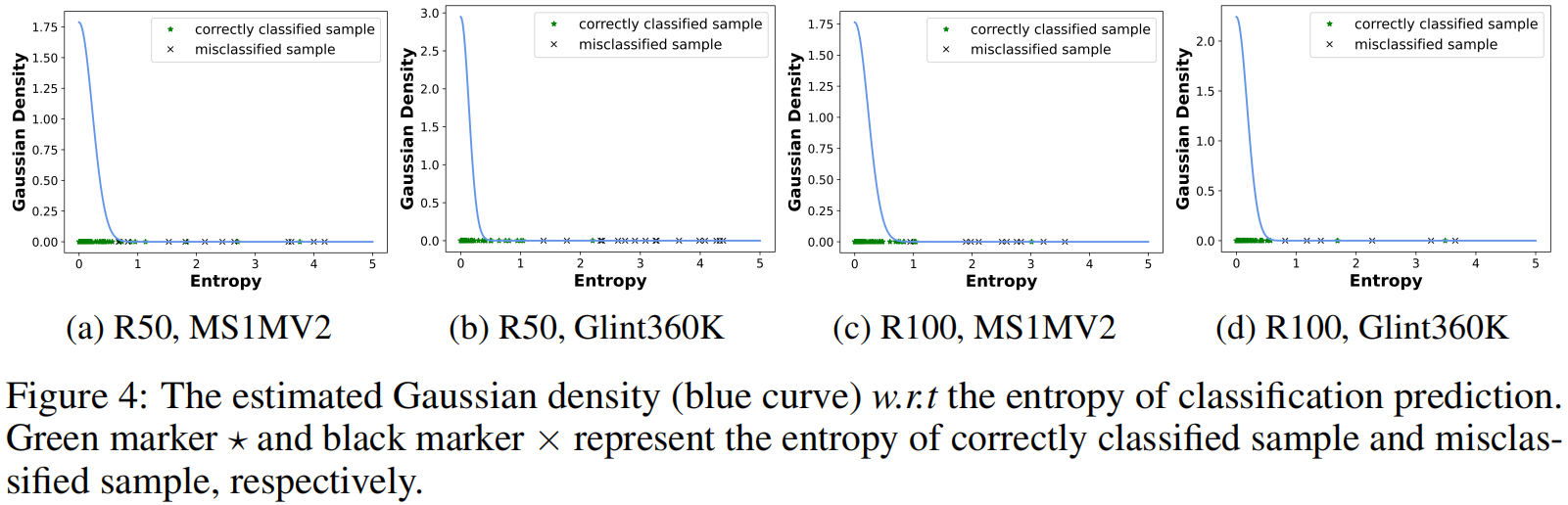
**图4: **模型训练过程中所估计的高斯密度(蓝色曲线)。绿色标记 ⋆ \textcolor{green}{\star} ⋆和黑色标记 × \times ×分别表示正确分类样本和错误分类样本的熵。
1.4 扰动引导的拓扑结构对齐策略的泛化性能
为表明此拓扑结构对齐策略 PTSA 在保持数据结构信息方面的一流泛化性能,我们在IJB-C测试集上调查了TopoFR模型与其变体TopoFR-A在输入空间与隐层空间上的拓扑结构差异,如下图5所示。值得一提的是,变体TopoFR-A直接利用持续同调技术来对齐两个空间的拓扑结构。
所得到的可视化统计结果明显地表明了我们所提出的扰动引导的拓扑结构对齐策略 PTSA 在保留数据结构信息方面的有效性和泛化性。

**图5:**TopoFR 和变体 TopoFR-A 在不同网络主干架构和训练数据集上的拓扑结构差异 [网络主干架构,训练数据集]。变体 TopoFR-A 直接利用 持续同调技术 对齐两个空间的拓扑结构。值得注意的是,我们使用 Glint360K 数据集训练的 TopoFR 模型在 IJB-C测试集 上几乎完美地对齐了输入空间和隐层空间的拓扑结构(即蓝色直方图几乎收敛为一条直线)。
五、结论
本文提出了一种人脸识别新框架TopoFR,其有效地将隐藏在输入空间中的结构信息编码到隐层空间,极大地提升了人脸识别模型在真实场景中的泛化性能。一系列在主流的人脸识别基准上的实验结果表明了我们TopoFR模型的SOTA性能。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容





所有评论(0)