16----桶计数法
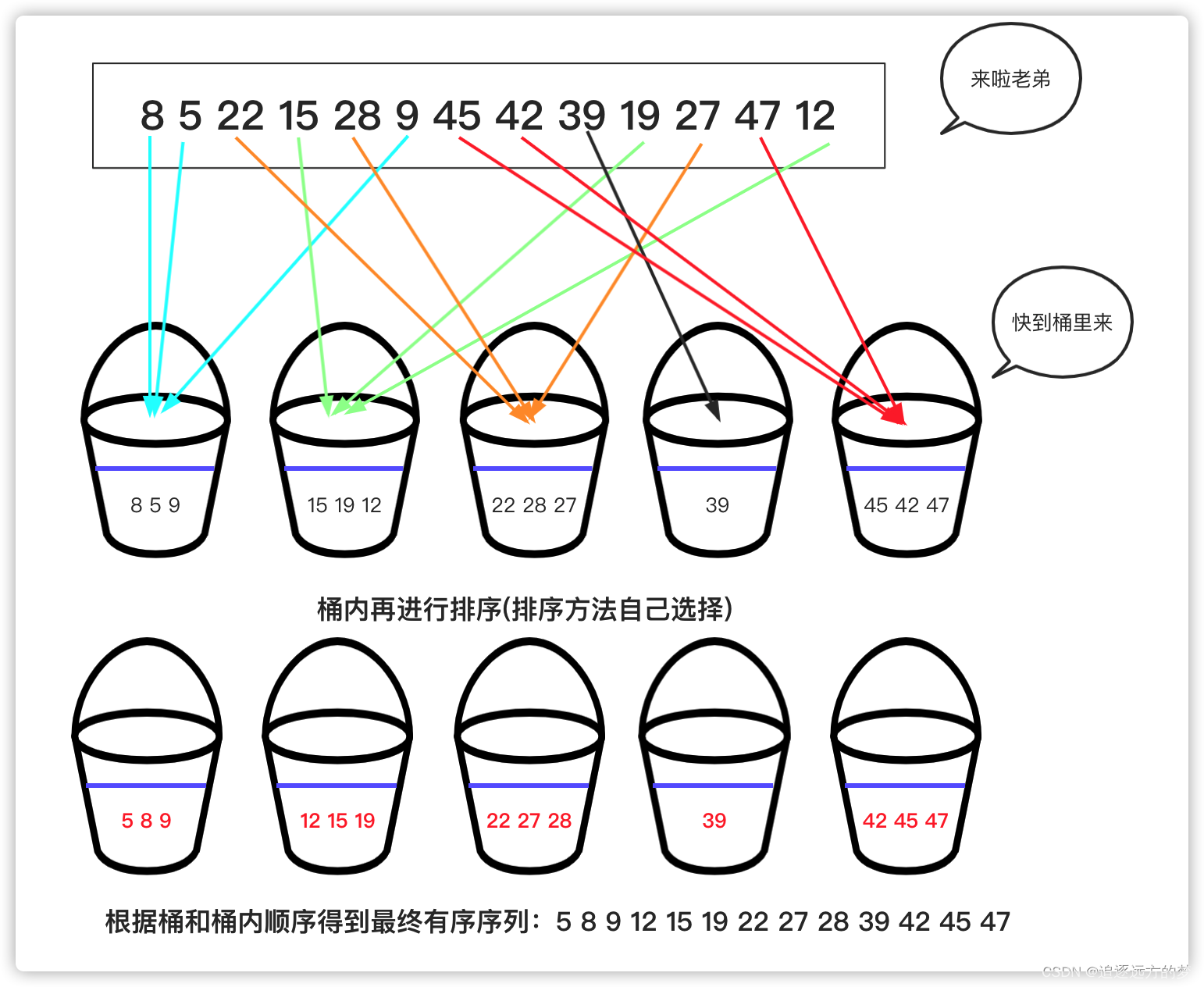
桶计数法(Bucket Counting)是一种常用的计数排序算法。它将待排序的元素分布到有限数量的桶(或容器)中,然后对每个桶中的元素进行排序(如果是一个桶,也可以不排),最后按照桶的顺序依次输出所有元素,即可得到排序结果。基本思想:假设待排序的元素是随机分布在一个已知范围内的整数,我们可以将这个范围划分为若干个大小相等的子区间,每个子区间对应一个桶。然后依次遍历待排序的元素,将每个元素放入对应
一、桶计数法:
桶计数法(Bucket Counting)是一种常用的计数排序算法。它将待排序的元素分布到有限数量的桶(或容器)中,然后对每个桶中的元素进行排序(如果是一个桶,也可以不排),最后按照桶的顺序依次输出所有元素,即可得到排序结果。

基本思想:假设待排序的元素是随机分布在一个已知范围内的整数,我们可以将这个范围划分为若干个大小相等的子区间,每个子区间对应一个桶。然后依次遍历待排序的元素,将每个元素放入对应的桶中。接着对每个桶中的元素进行排序,可以使用其他排序算法(如插入排序、快速排序等)或递归地应用桶计数法。最后按照桶的顺序,依次输出每个桶中的元素,即可得到排序结果。
桶计数法的时间复杂度取决于桶的数量和桶内元素的排序算法。如果桶的数量较大且每个桶内的元素较少,那么桶计数法的时间复杂度可以接近线性时间复杂度O(n)。但是,如果桶的数量较少或者每个桶内的元素较多,那么桶计数法的时间复杂度可能会接近O(nlogn)。
需要注意的是,桶计数法适用于待排序的元素满足一定的分布特性,例如均匀分布或近似均匀分布。如果元素的分布不均匀,可能会导致某些桶内的元素较多,从而影响排序的效率。因此,在使用桶计数法时,需要根据具体情况选择合适的桶的数量和分布方式,以获得较好的排序性能。
#include <stdio.h>
// 桶计数排序函数
void bucketSort(int arr[], int n) {
// 确定最大值和最小值
int min_val = arr[0];
int max_val = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] < min_val) {
min_val = arr[i];
}
if (arr[i] > max_val) {
max_val = arr[i];
}
}
// 计算桶的数量
int bucket_size = 5;
int bucket_count = (max_val - min_val) / bucket_size + 1;
// 创建桶
int buckets[bucket_count][n];
int bucket_sizes[bucket_count];
for (int i = 0; i < bucket_count; i++) {
bucket_sizes[i] = 0;
}
// 将元素放入桶中
for (int i = 0; i < n; i++) {
int index = (arr[i] - min_val) / bucket_size;
buckets[index][bucket_sizes[index]] = arr[i];
bucket_sizes[index]++;
}
// 对每个桶中的元素进行排序(可以使用其他排序算法)
for (int i = 0; i < bucket_count; i++) {
for (int j = 0; j < bucket_sizes[i]; j++) {
for (int k = 0; k < bucket_sizes[i] - j - 1; k++) {
if (buckets[i][k] > buckets[i][k + 1]) {
int temp = buckets[i][k];
buckets[i][k] = buckets[i][k + 1];
buckets[i][k + 1] = temp;
}
}
}
}
// 输出排序结果
int index = 0;
for (int i = 0; i < bucket_count; i++) {
for (int j = 0; j < bucket_sizes[i]; j++) {
arr[index] = buckets[i][j];
index++;
}
}
}
// 测试
int main() {
int arr[] = {29, 10, 14, 37, 13, 25, 16, 22};
int n = sizeof(arr) / sizeof(arr[0]);
bucketSort(arr, n);
printf("排序结果:");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
/*
上述代码中,首先确定待排序数组的最大值和最小值,然后根据桶的大小确定桶的数量。接下来创建二维数组`buckets`作为桶,并创建一维数组`bucket_sizes`记录每个桶中元素的数量。然后将待排序数组中的元素根据值的范围放入对应的桶中。接着对每个桶中的元素进行排序,这里使用了冒泡排序算法进行示例。最后将排序后的元素依次放回原数组中,即可得到排序结果。在示例中,桶的大小为5,所以元素范围在0-40之间,共计8个元素,被分为了8个桶。最终的排序结果为10 13 14 16 22 25 29 37。
*/二、其他应用:
除了利用桶计数法来排序以外,还可以用来记录输入,寻找相关规律。
下面我们以两道例题为主来进行相关讲解:
1:最长平台
题目描述
对于一个数组,其连续的相同段叫做一个平台,例如,在 1,2,2,3,3,3,4,5,5,6 中 1,2−2,3−3−3,4,5−5,6 都是平台。
编写一个程序,接收一个数组,找出最长的平台。在上面的例子中 3−3−3 就是最长的平台。
输入格式
第一行有一个整数 n,为数组元素的个数。(1≤n≤100)
第二行有 n 个整数,整数之间以一个空格分开,整数 k 范围(0<k<2000)。
输出格式
输出最长平台的长度。
输入输出样例
输入
10 1 2 2 3 3 3 4 5 5 6输出
3
显然这道题就可以利用桶计数法来快速实现,定义一个数组,将它视为桶组,然后遍历输入,将相同的数存到同一个桶中,从而记录出与当前数相同的数的个数,然后再循环遍历找到装的数最多的桶即可。
//最长平台
#include<iostream>
using namespace std;
int main(void)
{
int n;
cin >> n;
int a[101] = { 0 };
int b[101] = { 0 };
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
int j = 0;
for (int i = 1; i < n; i++)
{
if (a[i] == a[i - 1]) b[j] ++;
else j++;
}
int max=b[0];
for (int i = 0; i < j; i++)
{
if (b[i] > max) max = b[i];
}
cout<<max+1;
return 0;
}
最后max+1是因为存入桶的只是与当前数相同的数的个数,还要加上其本身。
2:整数去重
题目描述
给定含有 n 个整数的序列,要求对这个序列进行去重操作。所谓去重,是指对这个序列中每个重复出现的数,只保留该数第一次出现的位置,删除其余位置。
输入格式
输入包含两行:
第一行包含一个正整数 n(1≤n≤20000),表示第二行序列中数字的个数;
第二行包含 n 个整数,整数之间以一个空格分开。每个整数大于等于 10 、小于等于 100。
输出格式
输出只有一行,按照输入的顺序输出其中不重复的数字,整数之间用一个空格分开。
输入输出样例
输入
5 10 12 93 12 75输出
10 12 93 75
很明显,这道题也可以利用桶计数法:每读入一个数,就去判断存放该数的桶是否为空,若为空,则存放并记录;否则 只存放不记录(也可以不存放,但存放有一定的好处,可以同时记录所有数字的输入次数)。最后输出即可
//整数去重
#include<iostream>
using namespace std;
int main(void)
{
int n;
cin >> n;
int a[20001] = { 0 };
int b[20001] = { 0 };
int c[20001] = { 0 };
int j = 0;
for (int i = 0; i < n; i++)
{
cin >> a[i];
if (b[a[i]] == 0) c[j++] = a[i];
b[a[i]]++;
}
for (int i = 0; i < j; i++)
{
cout<<c[i]<<" ";
}
return 0;
}
/*
赋值号和等于号不要混淆
= ==
*/下面这个代码就是统计输入中每个数字出现的次数:(从0到max)
#include<iostream>
using namespace std;
int main(void)
{
int n;
cin >> n;
int a[100001] = { 0 };
int b[100001] = { 0 };
int max;
for (int i = 0; i < n; i++)
{
cin >> a[i];
if(i==0) max = a[0];
if (max < a[i]) max = a[i];
b[a[i]]++;
}
for (int i = 0; i <= max; i++)
{
cout << b[i] << endl;
}
return 0;
}
开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献10条内容
已为社区贡献10条内容





所有评论(0)