【深度学习】时序偏移归一化利器-RevIN
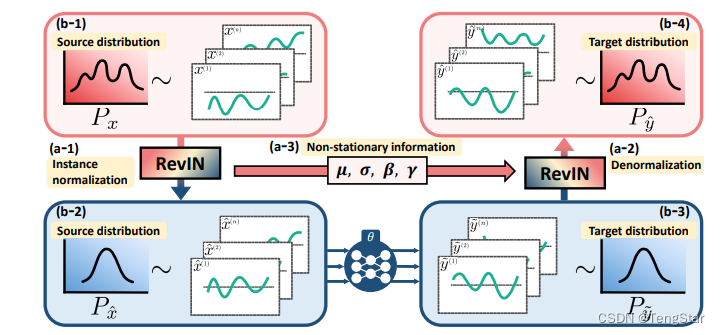
RevIN(Reversible Instance Normalization)是一种可逆的实例归一化方法。它不仅能对数据进行归一化处理,还能将归一化后的数据反归一化,恢复到原来的分布。这种方法特别适用于时间序列数据,因为它可以动态调整数据的归一化参数,以应对数据分布的变化。RevIN是一种强大的数据归一化技术,特别适用于时间序列数据。它不仅能对数据进行有效的归一化处理,还能将归一化后的数据恢复到
【深度学习】时序分布偏移归一化利器-RevIN
1. 引言
在深度学习中,数据归一化(Normalization)是一个常见且重要的预处理步骤,它能帮助模型更快地收敛,并提高模型的性能。然而,对于某些任务,如时间序列预测,数据的分布可能随时间变化,因此普通的归一化方法可能不够有效。为了解决这个问题,本文将介绍一种新的技术——Reversible Instance Normalization(RevIN),并详细解释其原理和实现方法。
2. 什么是RevIN?
RevIN(Reversible Instance Normalization)是一种可逆的实例归一化方法。它不仅能对数据进行归一化处理,还能将归一化后的数据反归一化,恢复到原来的分布。这种方法特别适用于时间序列数据,因为它可以动态调整数据的归一化参数,以应对数据分布的变化。
ICLR2022论文:https://openreview.net/pdf?id=cGDAkQo1C0p
github代码:https://github.com/ts-kim/RevIN
3. RevIN的数学原理
3.1 归一化
对于给定的输入数据 x ∈ R N × T × F \mathbf{x} \in \mathbb{R}^{N \times T \times F} x∈RN×T×F,其中 N N N 是批量大小, T T T 是时间步数, F F F 是特征数。我们首先计算输入数据的均值 μ \mu μ 和标准差 σ \sigma σ:
μ = 1 N × T ∑ i = 1 N ∑ t = 1 T x i , t \mu = \frac{1}{N \times T} \sum_{i=1}^N \sum_{t=1}^T x_{i,t} μ=N×T1i=1∑Nt=1∑Txi,t
σ = 1 N × T ∑ i = 1 N ∑ t = 1 T ( x i , t − μ ) 2 + ϵ \sigma = \sqrt{\frac{1}{N \times T} \sum_{i=1}^N \sum_{t=1}^T (x_{i,t} - \mu)^2 + \epsilon} σ=N×T1i=1∑Nt=1∑T(xi,t−μ)2+ϵ
然后,我们对数据进行归一化处理:
x ^ i , t = x i , t − μ σ \hat{x}_{i,t} = \frac{x_{i,t} - \mu}{\sigma} x^i,t=σxi,t−μ
3.2 仿射变换
为了增强模型的表达能力,RevIN还可以引入仿射变换参数 γ \gamma γ 和 β \beta β:
y i , t = γ x ^ i , t + β y_{i,t} = \gamma \hat{x}_{i,t} + \beta yi,t=γx^i,t+β
3.3 反归一化
在反归一化过程中,我们需要将归一化后的数据恢复到原来的分布:
x ^ i , t = y i , t − β γ \hat{x}_{i,t} = \frac{y_{i,t} - \beta}{\gamma} x^i,t=γyi,t−β
x i , t = x ^ i , t σ + μ x_{i,t} = \hat{x}_{i,t} \sigma + \mu xi,t=x^i,tσ+μ
4. RevIN的实现
下面我们将用PyTorch实现RevIN的前向和反向过程。
import torch
import torch.nn as nn
class RevIN(nn.Module):
def __init__(self, num_features: int, eps=1e-5, affine=True, subtract_last=False):
"""
:param num_features: 特征或通道的数量
:param eps: 数值稳定性参数,防止除零错误
:param affine: 如果为True,RevIN有可学习的仿射参数
:param subtract_last: 如果为True,减去最后一个时间步的值
"""
super(RevIN, self).__init__()
self.num_features = num_features
self.eps = eps
self.affine = affine
self.subtract_last = subtract_last
if self.affine:
self._init_params()
def forward(self, x, mode: str, mask=None):
if mode == 'norm':
self._get_statistics(x, mask)
x = self._normalize(x)
elif mode == 'denorm':
x = self._denormalize(x)
else:
raise NotImplementedError
return x
def _init_params(self):
# 初始化RevIN参数: (M,)
self.affine_weight = nn.Parameter(torch.ones(self.num_features))
self.affine_bias = nn.Parameter(torch.zeros(self.num_features))
def _get_statistics(self, x, mask=None):
dim2reduce = tuple(range(1, x.ndim - 1))
if self.subtract_last:
self.last = x[:, -1, :].unsqueeze(1)
else:
self.mean = torch.mean(x, dim=dim2reduce, keepdim=True).detach()
self.stdev = torch.sqrt(torch.var(x, dim=dim2reduce, keepdim=True, unbiased=False) + self.eps).detach()
def _normalize(self, x):
if self.subtract_last:
x = x - self.last
else:
x = x - self.mean
x = x / self.stdev
if self.affine:
x = x * self.affine_weight
x = x + self.affine_bias
return x
def _denormalize(self, x):
if self.affine:
x = x - self.affine_bias
x = x / (self.affine_weight + self.eps * self.eps)
x = x * self.stdev
if self.subtract_last:
x = x + self.last
else:
x = x + self.mean
return x
5. 代码详解
5.1 初始化参数
def __init__(self, num_features: int, eps=1e-5, affine=True, subtract_last=False):
...
self.num_features = num_features
self.eps = eps
self.affine = affine
self.subtract_last = subtract_last
if self.affine:
self._init_params()
初始化函数中定义了特征数、数值稳定性参数、仿射参数和是否减去最后一个时间步的参数。
5.2 前向传播
def forward(self, x, mode: str, mask=None):
if mode == 'norm':
self._get_statistics(x, mask)
x = self._normalize(x)
elif mode == 'denorm':
x = self._denormalize(x)
else:
raise NotImplementedError
return x
根据模式(归一化或反归一化)选择相应的处理方法。
5.3 归一化
def _normalize(self, x):
if self.subtract_last:
x = x - self.last
else:
x = x - self.mean
x = x / self.stdev
if self.affine:
x = x * self.affine_weight
x = x + self.affine_bias
return x
计算均值和标准差后,对数据进行归一化处理,并应用仿射变换。
5.4 反归一化
def _denormalize(self, x):
if self.affine:
x = x - self.affine_bias
x = x / (self.affine_weight + self.eps * self.eps)
x = x * self.stdev
if self.subtract_last:
x = x + self.last
else:
x = x + self.mean
return x
撤销仿射变换,乘以标准差,并加上均值或最后一个时间步的值,恢复原始数据分布。
6. 示例
假设我们有一个输入张量x,形状为(batch_size, seq_length, num_features)。我们定义一个RevIN模块并对数据进行归一化和反归一化处理:
import torch
# 假设输入数据形状为(batch_size, seq_length, num_features)
x = torch.randn(32, 100, 64) # batch_size=32, seq_length=100, num_features=64
# 创建RevIN模块
revin = RevIN(num_features=64, affine=True, subtract_last=False)
# 归一化
x_norm = revin(x, mode='norm')
# 反归一化
x_denorm = revin(x_norm, mode='denorm')
# 打印结果
print(f"输入数据形状: {x.shape}")
print(f"归一化后数据形状: {x_norm.shape}")
print(f"反归一化后数据形状: {x_denorm.shape}")
在这个例子中,我们首先创建一个随机的输入张量x,然后使用RevIN模块对其进行归一化和反归一化处理,并输出结果。通过这种方式,可以看到数据在归一化和反归一化过程中的变化。
————————————————————————————————————————————————
7. 总结
RevIN是一种强大的数据归一化技术,特别适用于时间序列数据。它不仅能对数据进行有效的归一化处理,还能将归一化后的数据恢复到原来的分布,为深度学习模型提供更稳定和有效的数据输入。在本文中,我们详细介绍了RevIN的数学原理和实现方法,希望对大家有所帮助。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容






所有评论(0)