
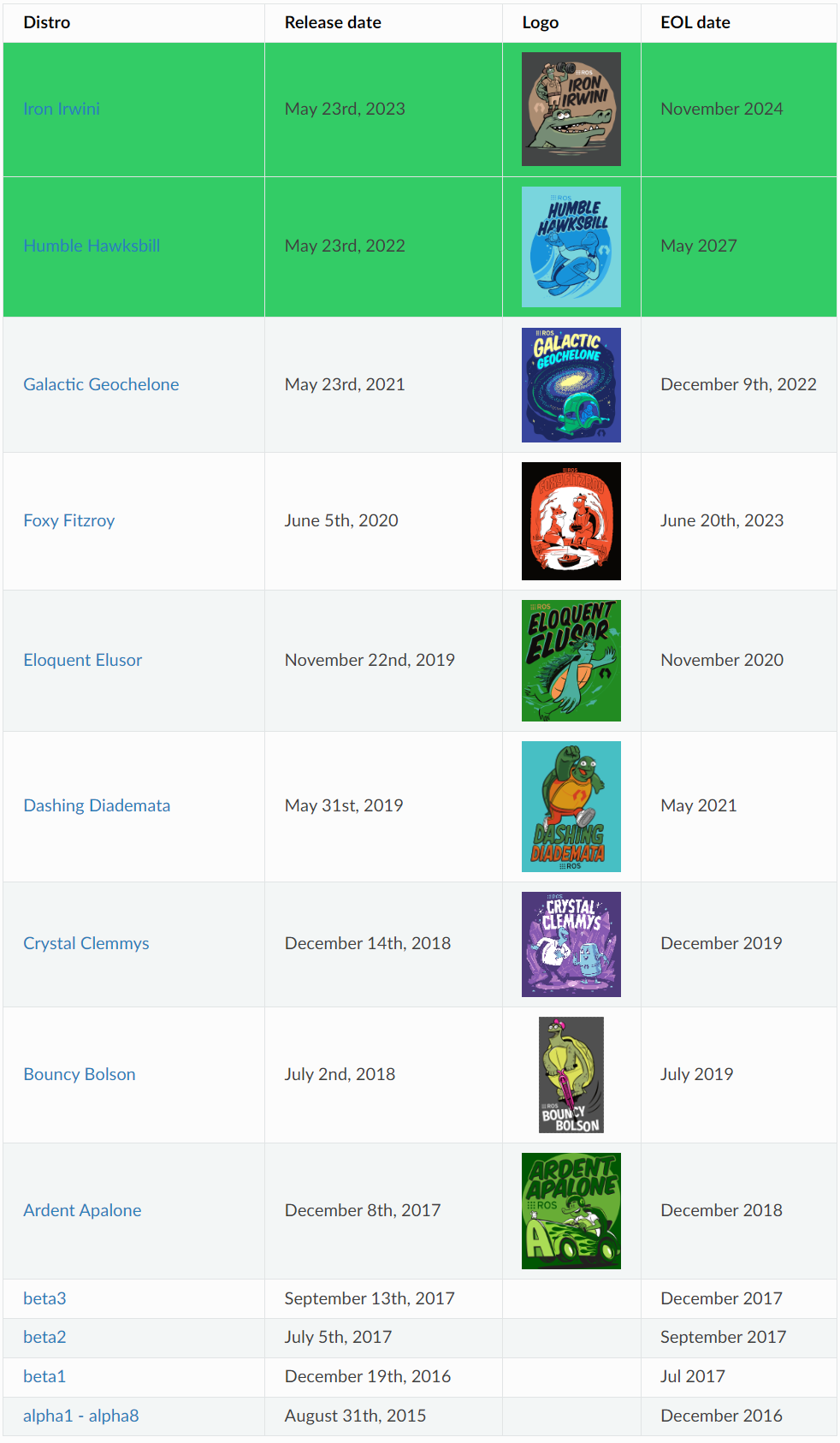
图论之邻接表
本文介绍了图的邻接表存储方法,使用邻接表存储图要稍微复杂一些,但能够提高空间利用率。本文给出了两种实现方法,一种是链式前向星,另一种是链表实现,链式前向星是利用数组来模拟链表,并且在最后给出了邻接表的一种打印方法。
路径规划系列文章目录
目录
一、邻接表
由于对于稀疏图来说,使用邻接矩阵进行存储显然会使得空间利用率较低,因此利用邻接表来存储图,可以克服这一缺点。
前面我们提到过,图其实就是由顶点和边构成的,因此我们可以将图分两部分来组织,即顶点与其连接的边。对于顶点而言,我们只需要存储顶点的信息以及边的地址,存储顶点信息代表着顶点的编号,有了边的地址就能够访问与其相连的边的信息,此外一般我们将顶点按照1,2,3...n来进行编号,这样可以将顶点表示为一个数组,只需要通过顶点编号对应位下标即可访问各个顶点。对于边来说,只需要存储边的权重,所连接的顶点编号以及下一条边的地址即可,因此边适合用链表来存储。
综上所述的分析,我们可以知道顶点表的要点主要有:
- 顶点表是一个数组,每个结点通过结点编号所对应的下标访问
- 结点中包含存储的顶点数据,这里是顶点编号
- 每个顶点表的结点中还包含其所对应边结点的地址,由于边是用链表来表示的,因此只需要知道与其相连的任意一条边结点的地址即可。
因此顶点表的结点如下图所示。

同样地,边链表的要点有:
- 边链表是链表构建成的
- 边链表中包含该边的权重
- 边链表中还包含另一个顶点信息,(由于边链表一定是根据某个顶点访问到的,因此在访问边链表前已经知道了一个顶点的信息,所以只需要在记录下另一个顶点的信息即可)
- 边链表中包含连接在该顶点上的下一条边的地址(以便访问下一条边)
因此边链表的结点如下图所示。

下面是一张图与其对应邻接表的示例:


二、邻接表实现
这里提供两种邻接表的实现方法,一种是链式前向星的方法,另一种是使用链表实现。下面分别介绍。
2.1 链式前向星实现
使用链式前向星其实就是利用两个数组来模拟链表实现邻接表,并且我们不但对顶点进行编号,我们还对边进行编号,因为每一条边都包含信息,相对于其他边都是独立的,因此我们可以将边也用数组来表示,并且使用其下标访问。
我们重点来介绍如何添加边的信息。我们使用head[]数组来表示头结点,如head[n] = a;表示头结点n的首个边的编号为a。用e[]结构体数组表示边结点。边界点存储了该边的权重、下一个结点的编号,以及下一条边的编号。其定义如下
const int M=500;//边的最大数量
struct Edge //边结结点构体
{
int to,w;//分别表示下一个顶点编号以及该条边的权重
int next;//下一条边的编号
}e[M];
我们从1开始对边结点进行编号,每添加一条边,编号就+1,添加时采用头插法添加,比如说当向第i个顶点上添加边的时候,只需要将新的边的next=head[i],然后将head[i]=新的边的编号即可。这里使用一个整型变量idx为其分配编号。


插入结束后,则链表状态如下所示

代码如下所示
#include<iostream>
#include<cstring>
using namespace std;
const int N=500;//顶点最大数量
const int M=500;//边的最大数量
const int INF = 1e9;//最大权重
int n;
int head[N];//顶点结点数组
int idx;//边结点的编号
struct Edge //边结结点构体
{
int to,w;//分别表示下一个顶点编号以及该条边的权重
int next;//下一条边的编号
}e[M];
void init()
{
memset(head,-1,sizeof(head));//将头结点指向第一个编号设置为-1
idx = 1;//边编号从1开始
}
void add(int a,int b,int w)//添加边
{
e[idx].to = b;//与边相连的另一个顶点编号
e[idx].w = w;//设置权重
e[idx].next = head[a];//边指向顶点a的下一条边的编号
head[a] = idx;//更新顶点a指向的边
idx++;//编号自增1
}
void testEdge()
{
int m;
cin>>n>>m;//输入顶点数量和边的数量
init();
int a,b,w;
while(m--)
{
cin>>a>>b>>w;
add(a,b,w);
}
/*按照结点打印图*/
for(int i=1;i<=n;i++)
{
cout<<i<<"->";
for(int j=head[i];j!=-1;j=e[j].next)
{
cout<<e[j].to<<"("<<e[j].w<<")"<<"->";
}
cout<<endl;
}
}
int main()
{
testEdge();
}2.2 链表实现
#include<iostream>
#include<queue>
#include<stack>
using namespace std;
#define INF 65333
#define MaxVerNum 1000 //定义最大顶点个数
typedef char elementType; //定义定点数据类型
typedef int einfoType; //定义权值数据类型
//边链表结点结构
typedef struct eNode
{
int adjVer; //边链表编号
einfoType einfo;//边链表边信息
struct eNode* next; //边链表下一个结点
}EdgeNode;//链表结点类型
typedef struct vNode
{
elementType data;//存放图中顶点数据值
EdgeNode* firstEdge;
}VerNode;//顶点表结点类型
class Graph
{
private:
VerNode* VerList;//结点
int VerNum;//顶点个数
int ArcNum;//边数
public:
void CreateGraph();
void printGraph();
};
void Graph::CreateGraph()
{
int vNum,aNum;
cin>>vNum>>aNum;//输入顶点数量和边数量
ArcNum = aNum;
VerNum = vNum;
VerList = new VerNode[VerNum+1];//给顶点表开辟空间
while(vNum)//初始化顶点表
{
VerList[vNum].data = 0;
VerList[vNum].firstEdge = NULL;
vNum--;
}
aNum = ArcNum;
while(aNum--)//输入图信息
{
int a,e,w;
cin>>a>>e>>w;
EdgeNode *en = new EdgeNode;
en->einfo = w;//给边付权重
en->adjVer = e;//设置另一个顶点编号
VerList[a].data = a;//设置该顶点编号
en->next = VerList[a].firstEdge;//该边结点下一个指向第一个边结点
VerList[a].firstEdge = en;//第一个边结点指向该边
}
}
void Graph::printGraph()
{
int vNum;
vNum = VerNum;
while(vNum)
{
EdgeNode* pe;
cout<<vNum<<"->";
for(pe = VerList[vNum].firstEdge;pe!=NULL;pe=pe->next)
{
cout<<pe->adjVer<<"("<<pe->einfo<<")->";
}
vNum--;
cout<<endl;
}
}
int main()
{
Graph g;
g.CreateGraph();
g.printGraph();
}
三、总结
本文介绍了图的邻接表存储方法,使用邻接表存储图要稍微复杂一些,但能够提高空间利用率。本文给出了两种实现方法,一种是链式前向星,另一种是链表实现,链式前向星是利用数组来模拟链表,并且在最后给出了邻接表的一种打印方法。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容





所有评论(0)