KAN 学习 Day1 —— 模型框架解析及 HelloKAN

不得不说，这个hellokan跑下来，真的很丝滑，而且感受到了作者团队的心思缜密，除了发挥模型自身的优势（理论上），还将模型优化、模型可视化、模型版本等细节都展示出来了。这也是我第一次使用ipynb跑模型，感受到了逐步运行的乐趣。目前在模型训练的体验上我对KAN产生了十分的好感，至于它的功能是否真的强大，还需要其他案例的测试。欢迎感兴趣的小伙伴一起交流！

小老弟来喽

1945人浏览 · 2024-09-02 21:16:46

小老弟来喽 · 2024-09-02 21:16:46 发布

说明

最近了解到了一个新东西——KAN，我的毕设导师给推荐的船新框架。我看过很多剖析其原理的文章，发现大家对其持有的观点都各不相同，有的说可以颠覆传统MLP，有的说可以和Transformer同等地位，但是也有人说它训练速度太慢，只不过是昙花一现。总之呢，既然是新模型，是否会成为人工智能行业的新方向，还得看它能不能经得住实验“严刑拷打”。我先跟进一波，了解为主。

论文原文：《KAN: Kolmogorov–Arnold Networks》

全文翻译：KAN: Kolmogorov–Arnold Networks 学术论文全译 - lsgxeva - 博客园 (cnblogs.com)

项目地址：KindXiaoming/pykan: Kolmogorov Arnold Networks (github.com)

2.2.3 Plot KAN at initialization

2.2.4 Train KAN with sparsity regularization

2.2.5 Prune KAN and replot

2.2.6 Continue training and replot

2.2.7 Automatically or manually set activation functions to be symbolic

2.2.8 Continue training till machine precision

2.2.9 Obtain the symbolic formula

2.3 总结

一、模型框架

论文原文我大概看了一点点，读了许多业界大佬写的分析文章，自我感觉啊，这个新框架理解难度不是特别大，KANs与MLPs最显著的区别：

MLPs 在节点（“神经元”）上放置固定的激活函数，而 KANs 在边缘（“权重”）上放置可学习的激活函数，如图0.1所示。因此，KANs 完全没有线性权重矩阵：相反，每个权重参数都被一个可学习的一维函数替代，作为样条进行参数化。
KANs 的节点只是简单地对传入信号进行求和，不应用任何非线性。

1.1 模型原理

如果 f 是定义在有界域上的多变量连续函数，那么 f 可以被写成单变量连续函数的有限组合以及加法的二元运算。

这个公式，直观上看就是一个多对一模型，输入是向量 $x$ ，多维度的，输出为分布运算再求和后的值。 $p,q$ 与输入向量的维度 $n$ 直接相关， $\phi _{q,p}$ 和 $\Phi _{q}$ 均为一维函数。

1.2 模型方程

这是一个KAN公式，与2.1非常相似，它经过 $L$ 次一维函数计算求和后进行输出。

1.3 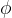$\phi$ 函数实现细节

（1）B样条函数（B-Spline）。这个我第一次接触应该是在计算机图形学，它的作用就是对曲线进行拟合，其中有一个控制点的概念，控制点越多，拟合效果越好。

在这里谈点个人见解，模型本质就是拟合，用数学函数去描述一个现象，这个函数可能是线性的、非线性的、简单的、复杂的、单变量、多变量等等，研究就是使用尽可能简单的模型去拟合尽可能复杂的现象，说不定这篇论文中的“单变量连续函数的有限组合以及加法的二元运算”方案真的有奇效！

（2）残差激活函数。包含一个基函数 $b(x)$ （类似于残差连接，感觉比MLP使用的偏执常数 $b$ 高级一点），使得激活函数 $\phi (x)$ 是基函数 $b(x)$ 和样条函数 $spline(x)$ 的和：

其中 $c_{i}$ 是可训练的。原则上， $w$ 是多余的，因为它可以吸收到 $b(x)$ 和 $spline(x)$ 中。然而，我们仍然包含这个 $w$ 因子来更好地控制激活函数的整体幅度。

(3) 初始化比例。每个激活函数的初始化设置为 $spline(x)\approx 0$ 。 $w$ 根据 Xavier 初始化进行初始化，这已经被用于初始化 MLP 中的线性层。

(4) 样条格更新。我们根据其输入激活实时更新每个格点，以解决样条函数在有界区域上定义，但在训练过程中激活值可能会演化出固定区域的问题。

1.4 KANs

原文指出，KAN可以像MLP一样直接进行了堆叠，包括模型的深度 $L$ 、输入输出的维度 $n_{in},n_{out}$ ，从而实现泛化，也就成了KANs。

然而，我们对科尔莫戈洛夫-阿诺尔德定理在机器学习中的用处更加乐观。首先，我们不必局限于原始的方程（2.1），该方程仅具有两层非线性和隐藏层中的少量项（2n + 1）：我们将将网络推广到任意宽度和深度。其次，科学和日常生活中的大多数函数通常是光滑的，并具有稀疏的组合结构，潜在地促进了光滑的科尔莫戈洛夫-阿诺尔德表示。

来看论文中的这个例子：

我们看到这个网络有三层，即 $L=3$ ，初始化每层维度： $[n_{0},n_{1},n_{2}]=[2,5,1]$ ，
第 0 层为输入节点： $[x_{0,1},x_{0,2}]$
第 1 层节点数目为 5，还是遵循了 $q=2n+1$ ，计算公式如下：

稍微翻译一下：

         $l$ 为层号： $[0,...,L-1]$ ；

         $i$ 为 $l$ 层节点的编号： $[1,...,n_{l}]$ ；

         $j$ 为 $l+1$ 层的节点编号 $[1,...,n_{l+1}]$ ；

第 0 层经过计算获得第 1 层，计算时 $l=0$ ，输入向量 $x$ 的两个维度，都经过5次一维 $\phi$ 计算，然后对应位置进行加和得到第 1 层 5 个节点的值。将公式写成矩阵的形式：

二、项目整体介绍

将项目clone到本地，配齐需要使用的环境，然鹅我并没严格按照作者的那一套，不想太麻烦，以后出了问题再研究。

2.1 目录

文件：

README.md：这个是项目的介绍，包括了KAN的简单介绍、安装、文档、教程、超参数优化建议、作者注等内容。
setup.py：安装项目python包的脚本
requirements.txt：项目依赖包的版本说明，在README.md文件中也有说明。
LICENSE：项目许可证
hellokan.ipynb：入门教程

文件夹：

kan：项目源码
- ~.py：源码
- .ipynb_checkpoints：测试文件
- experiments：实验
- assets：两张图片
docs：说明文档
pykan.egg-info：文件结构
tutorials：教程
- .ipynb_checkpoints：部分样例的测试文件
- API_demo：12个接口教程
- Community：2个实际案例
- Example：15个不同任务的案例
- Interp：11个插值案例
- Physics：4个物理案例

2.2 hellokan

作者在开始又叙述了一次定理，接着是模型的矩阵表示形式，对 $\Phi$ 函数进行了划分，其中 $\Phi _{in}$ 是对输入向量进行处理，将维度为 $n$ 的输入向量转化为 $2n+1$ 维的输出， $\Phi _{out}$ 则是对这个输出进行处理，将 $\Phi _{in}$ 的 $2n+1$ 维输出转化为 1 维。

然后作者介绍了KAN的两个特点：

KAN 只是 KAN 层的堆栈。
每个 KAN 层都可以可视化为一个全连接层，每个边缘上都放置了一个 1D 函数。

Get started with KANs

2.2.1 Initialize KAN

初始化KAN

from kan import *
torch.set_default_dtype(torch.float64)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)

# create a KAN: 2D inputs, 1D output, and 5 hidden neurons. cubic spline (k=3), 3 grid intervals (grid=3).
model = KAN(width=[2,5,1], grid=3, k=3, seed=42, device=device)

说明：

首先导入kan的全部模块，设置张量类型为 float64
检查GPU是否可用，输出可用设备名
使用 KAN()函数创建一个KAN实例：
- 尺寸为[2, 5, 1]，和上文中介绍的一致
- B样条曲线控制点为3个
- 网格间隔3，猜测和参数优化有关
- 设置随机种子42，保证多次运行结果相同
- 设置计算设备为device

运行：

cuda
checkpoint directory created: ./model
saving model version 0.0

我可以使用cuda加速运算，也就是说KAN是支持GPU的。然后产生了一个model，版本为 0.0，在主目录可以看到：

2.2.2 Create dataset

创建数据集

from kan.utils import create_dataset
# create dataset f(x,y) = exp(sin(pi*x)+y^2)
f = lambda x: torch.exp(torch.sin(torch.pi*x[:,[0]]) + x[:,[1]]**2)
dataset = create_dataset(f, n_var=2, device=device)
dataset['train_input'].shape, dataset['train_label'].shape

说明：

这段代码使用了kan.utils模块中的create_dataset函数来创建一个数据集。数据集是通过一个函数f生成的，该函数定义了数据点的生成方式。具体来说，函数f计算的是：

$f(x)=exp(sin(\pi \times x_{[0]})+x^{2}_{[1]})$

其中，x[0] 和 x[1] 是输入的二维特征。

代码解释：

from kan.utils import create_dataset：导入了kan.utils模块中的create_dataset函数。
f = lambda x: torch.exp(torch.sin(torch.pi*x[:,[0]]) + x[:,[1]]**2)：定义了一个匿名函数f，它接受一个二维张量x作为输入，并计算上述的函数表达式。
dataset = create_dataset(f, n_var=2, device=device)：使用create_dataset函数创建数据集，其中f是生成数据的函数，n_var=2指定了输入变量的数量，device=device指定了数据集应该在哪个设备上创建。

关于create_dataset函数，它通常用于生成模拟数据集，并可能包含以下参数：

f：生成数据的函数。
n_var：输入变量的数量。
device：数据集应该在哪个设备上创建。

在创建完数据集后，dataset变量将包含数据集的字典，其中包含以下键：

train_input：训练输入数据。
train_label：训练标签。

最后，代码尝试打印dataset['train_input'].shape和dataset['train_label'].shape，这两个表达式分别尝试获取训练输入数据和训练标签的形状。

运行：

(torch.Size([1000, 2]), torch.Size([1000, 1]))

2.2.3 Plot KAN at initialization

可视化初始化的KAN

# plot KAN at initialization
model(dataset['train_input']);
model.plot()

运行：

2.2.4 Train KAN with sparsity regularization

训练KAN

# train the model
model.fit(dataset, opt="LBFGS", steps=50, lamb=0.001);

参数说明：

dataset：这是要训练的数据集。
opt：指定了优化器。在这里，"LBFGS"代表Limited-memory Broyden–Fletcher–Goldfarb–Shanno（L-BFGS）优化算法，它是一种适用于小批量优化的优化算法，通常用于训练深度学习模型。
steps：指定了训练步骤的数量。这意味着模型将使用数据集进行50次迭代来优化其参数。
lamb：这个参数通常表示正则化项的系数，用于防止过拟合。在这里，它的值是0.001。

运行：

| train_loss: 1.85e-02 | test_loss: 1.77e-02 | reg: 6.93e+00 | : 100%|█| 50/50 [00:23<00:00, 2.10itsaving model version 0.1

输出了训练loss和测试loss等信息，并且更新模型版本至 0.1

说实话这是我第一见更新参数版本的模型。

2.2.5 Plot trained KAN

可视化训练后的结果：

model.plot()

运行：

输出训练结果，看起来只用到了部分节点。

2.2.5 Prune KAN and replot

模型压缩并再次输出

model = model.prune()
model.plot()

对模型执行两个操作：

model = model.prune(): 这个操作通常用于模型压缩，特别是通过剪枝（pruning）来减少模型的参数量。剪枝可以去除模型中权重较小（通常是接近于零的权重）的神经元或者连接，从而达到压缩模型大小、降低计算成本和减少过拟合风险的目的。在执行剪枝后，模型的参数量和计算复杂度都会降低。
model.plot(): 这个操作用于可视化模型的某些属性或结果。具体可视化的内容取决于模型的类型和上下文。对于神经网络模型，这可能包括可视化模型的结构（例如神经元和层的数量）、损失函数随训练迭代的变化情况、模型的预测结果分布等。通常，这个函数需要依赖特定的库来实现，比如TensorFlow的tf.keras.Model类可能使用plot方法来绘制模型结构图。

运行：

saving model version 0.2

保存了新版本，并输出了剪枝后的可视化图片。

2.2.6 Continue training and replot

再次训练

model.fit(dataset, opt="LBFGS", steps=50);

运行：

| train_loss: 1.79e-02 | test_loss: 1.72e-02 | reg: 7.65e+00 | : 100%|█| 50/50 [00:17<00:00, 2.80itsaving model version 0.3

对比第一次输出：

| train_loss: 1.85e-02 | test_loss: 1.77e-02 | reg: 6.93e+00 | : 100%|█| 50/50 [00:23<00:00, 2.10itsaving model version 0.1

损失有略微减小，训练时间也减短了，并且保存为 0.3 版本

model = model.refine(10)

说明：

模型调优，传入参数10，目前还不知道如何实现，等解读源码时再研究

运行：

saving model version 0.4

模型又更新了一个版本

model.fit(dataset, opt="LBFGS", steps=50);

说明：

模型调优后又进行了一次训练，应该是用来对比调优的性能

运行：

| train_loss: 4.67e-04 | test_loss: 4.73e-04 | reg: 7.66e+00 | : 100%|█| 50/50 [00:16<00:00, 3.00itsaving model version 0.5

和调优前对比：

| train_loss: 1.79e-02 | test_loss: 1.72e-02 | reg: 7.65e+00 | : 100%|█| 50/50 [00:17<00:00, 2.80itsaving model version 0.3

这性能提升了不是一点点哇，直接提高了两个数量级，但是拟合情况存疑，有过拟合的风险。

2.2.7 Automatically or manually set activation functions to be symbolic

自动或手动将激活函数设置为符号

mode = "auto" # "manual"

if mode == "manual":
    # manual mode
    model.fix_symbolic(0,0,0,'sin');
    model.fix_symbolic(0,1,0,'x^2');
    model.fix_symbolic(1,0,0,'exp');
elif mode == "auto":
    # automatic mode
    lib = ['x','x^2','x^3','x^4','exp','log','sqrt','tanh','sin','abs']
    model.auto_symbolic(lib=lib)

代码解释：

mode = "auto" 或 mode = "manual"：这里定义了一个变量mode，它可以是"auto"或"manual"，用来控制后续代码执行的路径。
if mode == "manual":
- 如果mode的值是"manual"，则进入manual模式块。
- 在manual模式中，model.fix_symbolic(0,0,0,'sin');、model.fix_symbolic(0,1,0,'x^2');和model.fix_symbolic(1,0,0,'exp');这些语句被调用。
  - model.fix_symbolic方法看起来是用来在模型中固定某些符号表达式。参数的含义如下：
    - 第一个0可能表示固定的是输入的第一个变量。
    - 第二个0可能表示固定的是第二个变量的指数，这里为0意味着不使用该变量。
    - 第三个0可能表示固定的是第三个变量的指数，这里同样为0意味着不使用该变量。
    - 'sin'、'x^2'和'exp'分别是固定的符号表达式，分别代表正弦、平方和指数函数。
elif mode == "auto":
- 如果mode的值是"auto"，则进入auto模式块。
- 在auto模式中，定义了一个符号库lib，包含了可能的符号表达式，如['x','x^2','x^3','x^4','exp','log','sqrt','tanh','sin','abs']。
- 然后调用model.auto_symbolic(lib=lib)，这个方法可能用于自动选择或应用库中定义的符号表达式。

运行：

fixing (0,0,0) with sin, r2=0.9999999186941056, c=2
fixing (0,1,0) with x^2, r2=0.9999999824464364, c=2
fixing (1,0,0) with exp, r2=0.9999999908233412, c=2
saving model version 0.6

似乎是进行了三组设置：

fixing() 表示三个量的使用
with后跟激活函数类型
r2：这个应该是评估模型的拟合情况，在机器学习随机森林类中有这个评估方法
c：这个值不知道含义

然后保存模型版本 0.6

2.2.8 Continue training till machine precision

继续训练直到机器精度

model.fit(dataset, opt="LBFGS", steps=50);

运行：

| train_loss: 6.53e-10 | test_loss: 1.44e-10 | reg: 0.00e+00 | : 100%|█| 50/50 [00:05<00:00, 8.93itsaving model version 0.7

这个精度，我只能倒吸一口凉气，没怎么见过，但是测试的损失比训练损失小，这个情况也很少见。

2.2.9 Obtain the symbolic formula

获取符号公式

from kan.utils import ex_round

ex_round(model.symbolic_formula()[0][0],4)

运行：

$1.0e^{1.0x^{2}_{2}+1.0sin(3.1416x_{1})}$

体现了模型的可解释性

2.2.10 文件生成

每一个阶段（训练、压缩、调优、设置激活函数）都会产生过程文件，不同版本的model

history.txt

### Round 0 ###
init => 0.0
0.0 => fit => 0.1
0.1 => prune => 0.2
0.2 => fit => 0.3
0.3 => refine => 0.4
0.4 => fit => 0.5
0.5 => auto_symbolic => 0.6
0.6 => fit => 0.7