目录

一. 引入RNN

1.1 前馈神经网络

1.2 RNN简介

​编辑 二、RNN

 2.1 1vN结构

2.2 Nv1结构 

2.3 seq2seq结构 

2.3.1 Encoder部分

2.3.2 Deconder部分

---

一. 引入RNN

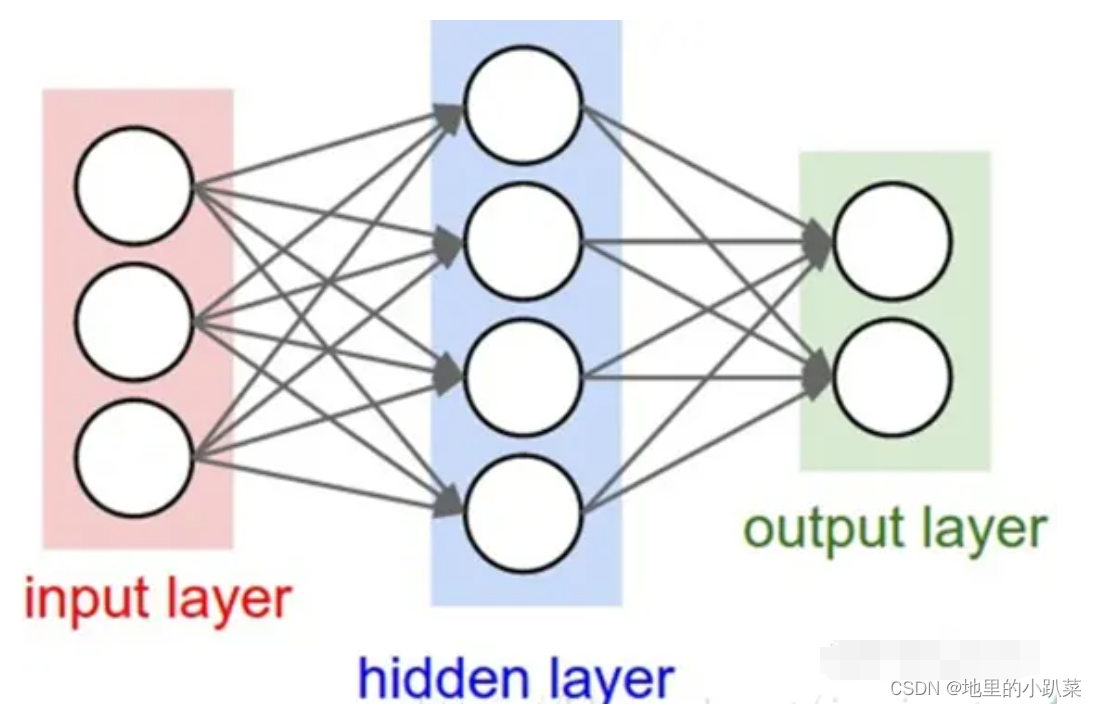
1.1 前馈神经网络

如下所示：

其正向传播过程为：

 

        通过上述计算过程我们发现,在前馈神经网络中，信息的传递是单向的， 这种限制虽然使得网络变得更容易学习，但在一定程度上也减弱了神经网络模型的能力。在生物神经网络中， 神经元之间的连接关系要复杂得多。前馈神经网络可以看作一个复杂的函数， 每次输入都是独立的， 即网络的输出只依赖于当前的输入。

        but在很多情况下，网络的输出不仅和当前时刻的输入相关， 也和其过去一段时间的输出相关。比如一个有限状态自动机， 其下一个时刻的状态（输出）不仅和当前输入相关， 也和当前状态（上一个时刻的输出）相关。此外， 前馈神经网络难以处理时序数据，比如视频、语音、文本等。时序数据的长度一般是不固定的，而前馈神经网络要求输入和输出的维数都是固定的，不能任意改变。 因此，当处理这一类和时序数据相关的问题时，就需要一种能力更强的模型。

1.2 RNN简介

        循环神经网络（Recurrent Netural Network,Rnn)是一类具有短期记忆能力的神经网络。在RNN中，神经元不但可以接受其他神经元的信息，也可以接受自身的信息，形成具有环路的网络结构，RNN由此得名。循环神经网络已经被广泛应用在语音识别、语言翻译以及图片描述等任务上。

        为了处理时序数据并利用其历史信息，我们需要让网络具有短期记忆能力。而前馈网络是一种静态网络，不具备这种记忆能力。

RNN基本结构如下：

 

 二、RNN

RNN的五种结构，如下图所示：

 

RNN分为一对一、一对多、多对一、多对多，其中多对多分为两种。

1. 单个神经网络，即一对一。
2. 单一输入转为序列输出，即一对多。这类RNN可以处理图片，然后输出图片的描述信息。
3. 序列输入转为单个输出，即多对一。多用在电影评价分析。
4. 编码解码(Seq2Seq)结构。seq2seq的应用的范围非常广泛，语言翻译，文本摘要，阅读理解，对话生成等。
5. 输入输出等长序列。这类限制比较大，常见的应用有作诗机器人。

一个经典的RNN如下图所示：

 h为隐状态，ℎ𝑡−1可以被看做一个记忆特征，提取了前t-1个时刻的输入特征。f为非线性激活函数，U，W，b，V都是网络参数。值得注意的是，无论进行到什么状态，所有的网络参数都是一样的，这也是权值共享的体现。

 2.1 1vN结构

1vN结构就是一个输入多个输出，它有如下两种常见结构：

第一种：

一个输入只输送给RNN第一个神经元，其表达式为：

ℎ1=𝑓(𝑈𝑥+𝑊ℎ0+𝑏)

ℎ𝑁=𝑓(𝑊ℎ𝑁−1+𝑏)

𝑦𝑡=𝑣ℎ𝑡

 第二种：

 

一个输入x输送给所有神经元，其表达式为：

ℎ1=𝑓(𝑈𝑥+𝑊ℎ0+𝑏)

ℎ𝑁=𝑓(𝑈𝑥+𝑊ℎ𝑁−1+𝑏)

𝑦𝑡=𝑣ℎ𝑡

2.2 Nv1结构 

Nv1结构就是多个输入一个输出，如下所示：

 

每一个神经元对应不同的输入，其表达式为：

ℎ1=𝑓(𝑈𝑥1+𝑊ℎ0+𝑏)

ℎ𝑁=𝑓(𝑈𝑥𝑁+𝑊ℎ𝑁−1+𝑏)

𝑦𝑡=𝑣ℎ𝑡

2.3 seq2seq结构 

seq2seq结构，即输入输出不等长的多对多结构，又叫Encoder-Decoder模型。

如上图所示，在Seq2Seq结构中，编码器Encoder把所有的输入序列编码成一个统一的语义向量Context，然后再由解码器Decoder解码。在解码器Decoder解码的过程中，不断地将前一个时刻的输出作为后一个时刻的输入，循环解码，直到输出停止符为止。

根据得到Context后Decoder的方式，可以将seq2seq分为以下几种常见形式：

以及： 

 

以及：

 

可以看到，三种形式中前半部分Encoder是一样的，不同之处在于得到语义向量Context之后Deconder的部分。

2.3.1 Encoder部分

Encoder部分都是一样的，Encoder的RNN接受输入x得到一个输出c，中间隐状态都没有进行输出。

 

c可以经多种方式得到：

 

Encoder结果c可以直接是最后一个神经元的隐状态ℎ4；也可以在ℎ4的基础上做一些变换得到，比如𝑞(ℎ4)；最后当然也可以使用所有神经元的隐藏状态进行变换得到。

2.3.2 Deconder部分

解码器是三种seq2seq的不同之处，下面依次介绍。

第一种：

与传统的RNN结构相比我们可以看到，这种形式下的Decoder部分将编码结果Context当成了RNN的初始隐藏状态ℎ0，接下来每一个神经元都都没有接受输入，并且每一个隐状态都进行了输出，根据上述经典RNN的公式，我们可以推出此种Decoder的表达式如下：

ℎ1′=𝑓(𝑈𝑥1+𝑊𝑐+𝑏)=𝑓(𝑊𝑐+𝑏)

ℎ𝑀′=𝑓(𝑈𝑥𝑀+𝑊ℎ𝑀−1+𝑏)=𝑓(𝑊ℎ𝑀−1+𝑏)

𝑦𝑡=𝑣ℎ𝑡

由于没有输入x，所以参数U不起作用。

第二种：

这种情况下Context不再作为初始隐状态，而是作为一个输入x送到所有神经元，公式如下所示：

ℎ1′=𝑓(𝑈𝑥1+𝑊ℎ0′+𝑏)=𝑓(𝑈𝑐+𝑊ℎ0′+𝑏)

ℎ𝑀′=𝑓(𝑈𝑥𝑀+𝑊ℎ𝑀−1+𝑏)=𝑓(𝑈𝑐+𝑊ℎ𝑀−1+𝑏)

𝑦𝑡=𝑣ℎ𝑡

第三种：

第三种与第二种相比，输入不再只是c，还增加了上一个神经元的输出y，所以公式如下：

ℎ1′=𝑓(𝑈𝑐+𝑊ℎ0′+𝑣𝑦0′+𝑏)

ℎ𝑀′=𝑓(𝑈𝑐+𝑊ℎ𝑀−1+𝑣𝑦𝑀−1′+𝑏)

𝑦𝑡=𝑣ℎ𝑡