【intro】Graph Isomorphism Network(GIN)
图神经网络(gnn)是一种有效的图表示学习框架。gnn采用邻域聚合方案,通过递归聚合和变换相邻节点的表示向量来计算节点的表示向量。已经提出了许多GNN变体,并在节点和图分类任务上取得了最先进的结果。然而,尽管gnn彻底改变了图表示学习,但人们对其表示特性和局限性的理解有限。->一个理论框架,用来分析GNN捕获不同图结构的能力。
论文
https://arxiv.org/pdf/1810.00826
abstract
图神经网络(gnn)是一种有效的图表示学习框架。gnn采用邻域聚合方案,通过递归聚合和变换相邻节点的表示向量来计算节点的表示向量。已经提出了许多GNN变体,并在节点和图分类任务上取得了最先进的结果。然而,尽管gnn彻底改变了图表示学习,但人们对其表示特性和局限性的理解有限。->一个理论框架,用来分析GNN捕获不同图结构的能力。
introduction
使用图结构数据进行学习,例如分子、社会、生物和金融网络,需要有效地表示它们的图结构。
GNN广泛遵循递归邻域聚合(或消息传递)方案,其中每个节点聚合其邻居的特征向量以计算其新的特征向量。经过k次聚合迭代后,节点由变换后的特征向量表示,特征向量捕获节点k- hop邻域内的结构信息。然后可以通过池化获得整个图的表示,例如,通过将图中所有节点的表示向量相加。
首先将给定节点的邻居的特征向量集表示为一个multiset,即一个可能含有重复元素的集合。那么,gnn中的邻居聚合可以看作是multiset上的聚合函数。(没明白)因此,为了具有强大的表示能力,GNN必须能够将不同的多集聚合成不同的表示。multiset函数的判别性越强,底层GNN的表示能力就越强。
文章的主要贡献:
- 证明了GNN在图结构的识别上最多和WL测试一样强大。
- 建立了邻居聚合(neighbor aggregation)和图读出函数(graph readout functions)的条件,在此条件下,所得的GNN与WL测试一样强大
- 识别了流行的GNN变体,如gcn 和GraphSAGE无法区分的图结构,并且精确地描述了基于GNN的模型可以捕获的图结构类型。
- 图同构网络(GIN),其判别/表征能力等于WL测试的能力。
preliminaries
notation介绍
表示图,图的节点特征向量被表示为
。有两个task:
- node classification。每一个节点
都有一个与之相关的标签
。这一个任务的目标是学习一个节点
的向量表示
,可以把
的标签预测为
- graph classification。给定一系列图
,图的标签为
,目标是学一个向量表示
来帮助预测整张图的标签
graph neural networks
GNNs使用图结构和节点特征来学习一个节点(
)或者整张图(
)的向量表示。GNN遵循邻域聚合策略,通过聚合其邻居的表示来迭代更新节点的表示。经过k次聚合迭代后,节点的表示捕获其k-hop网络邻居中的结构信息。GNN的第k层可以表示为:
这里是节点
在第
次迭代(层)的特征向量。我们将第0层初始化
。
表示的是一些列邻近
的节点。在GNN中,选择
和
十分重要。

(这一段不翻译了,前面已经在别的论文中看一遍了)
Weisfeiler-Lehman test
图同构问题是指两个图在拓扑上是否相同。除了一些极端情况,图同构的Weisfeiler- lehman (WL)检验是一种有效的、计算效率高的检验,可以区分一大批图(Babai & kuucera, 1979)。它的一维形式,“naïve vertex refinemen”,类似于GNN中的邻居聚合。
wl测试迭代地(1)聚合节点及其邻域的标签,(2)将聚合的标签散列成唯一的新标签。如果在某一次迭代中两个图的节点的标签不同,就认为这两张图是非同构的。
theoretical framework: overview

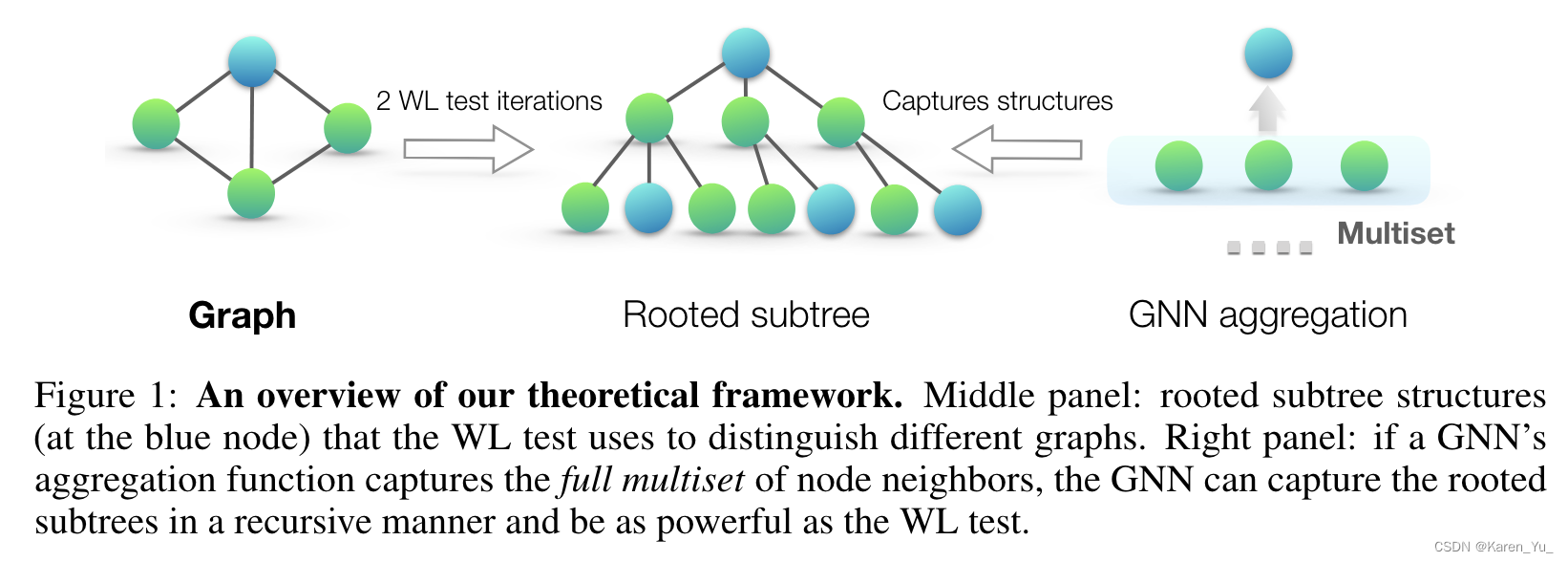
GNN递归地更新每个节点的特征向量,以捕获其周围其他节点的网络结构和特征,即其根子树结构(图1)。为了简化标记,我们可以在{a, b, c…}中为每个特征向量分配一个唯一的标签。然后,一组相邻节点的特征向量形成一个multiset(图1):同一元素可以出现多次,因为不同节点可以有相同的特征向量。
定义1 Multiset
multiset是集合的广义概念,它允许其元素有多个实例,即,一个multiset是一个2-tuple(二元),这里S是由
的离散元(distinct elements,指在集合中不重复的元素)组成的基础集合(underlying set,在数学中,指一个拓扑空间的基本元素组成的集合。)而
赋予了元素的多重性.
一个最强大的GNN只有在两个节点具有相同的子树结构并在相应节点上具有相同的特征时才能将两个节点映射到相同的位置。由于子树结构是通过节点邻域递归地定义的(图1),我们可以将分析简化为GNN是否将两个邻域(即两个多集)映射到相同的embedding或表示。最强大的GNN永远不会将两个不同的邻域(即多组特征向量)映射到相同的表示,这意味着它的聚合方案必须是单射的(injective)。
building powerful graph neural networks
理想情况下,最强大的GNN可以通过将不同的图结构映射到嵌入空间中的不同表示来区分不同的图结构。然而,这种将任意两个不同的图映射到不同嵌入的能力意味着要解决具有挑战性的图同构问题。也就是说,我们希望同构图映射到相同的表示,而非同构图映射到不同的表示。
lemma 2
令和
为两个非同构图,若存在一个图神经网络
将
和
映射到不同的embedding,Weisfeiler-Lehman图同构检验同样会认为
和
为两个非同构图。

因此,任何基于聚合的gnn在区分不同图方面最多与WL测试一样强大。一个自然的后续问题是,原则上是否存在与WL测试一样强大的gnn?->可,只要邻居聚合和图级读出函数是单射的,那么得到的GNN和WL测试一样强大。
Therorem 3
令为一个图神经网络,在足够的GNN层数下,如果满足以下条件,
将任意Weisfeiler-Lehman检验判定为非同构的图
和
映射到不同的嵌入:
1)A通过迭代地聚合和更新节点特性,其中
是作用于multiset的函数,
是单射的。
2)的graph-level readout,即在multiset的节点特征
上做操作的,是单射的。
(稍微断一下,什么是injective,单射, One to one Function)
lemma 4
假设输入特征空间是可数的。令
为GNN的第
层确定参数的函数(
)。其中
是被定义在有固定大小的multiset
上的。
的范围,即节点隐藏特征的空间
,对于
同样也是可数的。
除了区分不同的图之外,GNN还有一个重要的好处值得讨论,即捕获图结构的相似性。注意,WL测试中的节点特征向量本质上是单热编码,因此无法捕获子树之间的相似性。相比之下,满足theorem 3标准的一个GNN通过学习将子树嵌入到低维空间来推广WL检验。这使得GNN不仅可以区分不同的结构,还可以学习将相似的图结构映射到相似的嵌入,并捕获图结构之间的依赖关系。
Graph Isomorphism Network(GIN)
为了对邻域聚集的单射multiset函数建模,提出了“deep multisets”理论,即用用通用的multiset 函数来参数话神经网络。
lemma 5
假设是可数的。存在一个函数
使得
对于每个固定大小的multi set
是独特的。此外,任何multiset函数
对于一些函数
可以分解为
deep multisets和集合之间的一个重要区别是,某些流行的单射集函数,如均值聚集器,不是单射multiset函数。
corollary 6
假设是可数的。存在一个函数
,因此对于无穷多选择的
(包含所有无理数),对于每一对
(这里
,是multiset的固定大小),
都是独特的。此外,任何函数
对于一些函数
使用
对都可以分解成
可以使用多层感知机来学习和
graph-level readout of GIN
通过GIN学习的节点嵌入可以直接用于节点分类和链路预测等任务。对于图分类任务,提出以下“readout”函数,给定单个节点的嵌入,生成整个图的embedding。
随着迭代次数的增加,对应于子树结构的节点表示会变得更加精细和全局。足够的迭代次数是获得良好判别能力的关键。然而,来自早期迭代的特性有时可能会更好地泛化。为了考虑所有的结构信息,使用来自模型的所有深度/迭代的信息。我们通过类似于“Jumping Knowledge Network”的架构来实现这一点。
Less powerful but still interesting GNNs
与使用mlp的模型不同,1层感知器(即使带有偏置项)不是多集函数的通用逼近器。因此,即使具有1层感知器的gnn可以在某种程度上将不同的图嵌入到不同的位置,这种嵌入可能无法充分捕获结构相似性,并且对于简单分类器(例如线性分类器)来说很难拟合。


平均池化和最大池化不能区分结构。
这一节在描述之前的一些池化trick的使用结论。
下面是其他博客的摘录(老实说,到了图之后,才发现相关的文章少了很多,相比于CV和NLP)
论文阅读_图神经网络GIN - 知乎
之前研究方法着重于表示节点,引文着眼于表征图的结构。作者认为之前方法难以区分不同的图结构,并提出了一种基于GNN的方法GIN,它的区分效果与WL-Test效果相当。
一般情况下一个节点的表式通过聚合它k跳之内的邻近节点计算,而全图的表示则通过对所有节点的池化计算。文中使用了WL-test方法,即图同构测试,它是一个区分网络结构的强效方法,也是通过迭代聚合邻居的方法来更新节点,它的强大在于使用了injective(见后)聚合更新方法。而这里要评测GNN是否能达到类似WL-test的效果。
文中还使用了多合集multiset的概念,指可能包含重复元素的集合。


如图-1所示,有一个图(左图),如果想表征其中的蓝色节点,且只考虑两跳;计算方法如中图所示(子树); 通过迭代,变成了右图所示,每个节点只考虑其邻居,计算邻居时,再考虑邻居的邻居。
算法需要满足injective,injective可译为内射,即可把不同的元素映射成不同输出,在图结构中,不同的邻居结构需要生成不同的节点表征,而max,mean池化显然都不是injective的(后详述)。

平均池化和最大池化都不是内射的。
图-2展示了在多合集情况下,sum的效果最好,mean次之,max最差。
图-3中不同颜色表示不同实体,其中图2-a中两图结构不同,但平均池化和最大池化不能加以区分,而求和可以区分;图-2b中平均池化可区分两图,但最大池化取红与绿中最大值不能区分两图;同理,使用平均池化和最大池化也不能区分图-3c中的两个图。
How Powerful are Graph Neural Networks? GIN 图同构网络 ICLR 2019 论文详解-CSDN博客
文中提出了一个理论框架去分析GNNs的表达能力。在学习表示和区分不同的图结构时,描述了不同GNN变体的表达能力。Weisfeiler-Lehman 图同构测试(1968)(WL)是一种强大的检验方法,可以区分大量的图。与GNNs类似,WL测试通过聚集网络邻居的特征向量迭代地更新给定节点的特征向量。WL测试之所以如此强大,是因为它的单射聚合更新将不同的节点邻居映射到不同的特征向量。作者的主要观点是,如果GNN的聚合方案具有高度表达性,并且能够对单射函数建模,那么GNN可以具有与WL测试同样大的区分能力。
(将节点邻居映射到不同的特征向量,这与之前的很多GNN的目的都差不太多的样子,前面的可能是计算、卷积、这里可能偏重函数形式?)
为了在数学上形式化上述观点,文中提出的框架首先将给定节点的邻居的特征向量集表示为一个multiset,即,一个可能有重复元素的集合。然后,可以将GNNs中的邻居聚合看作是multiset上的聚合函数。因此,为了拥有强大的表示能力,GNN必须能够将不同的multiset聚合到不同的表示中。文中严格地研究了multiset函数的几个变体,并从理论上描述了它们的区分能力,即,不同的聚合函数如何区分不同的multiset。multiset函数的判别能力越强,GNN的表示能力就越强。
(我其实没太明白为什么要使用multiset,是说邻居的聚合方式可能是重复的,如果结构一样的话?)
GNNs的表达能力是捕获图结构的关键。文中通过在图分类数据集上的实验来验证理论,对比了使用各种聚合函数的GNNs的性能。
实验结果表明,在作者的理论中最强大的GNN,即图同构网络(GIN),根据经验判断也具有很高的表示能力,因为它几乎完全适合训练数据,而较弱的GNN变体往往严重不适合训练数据。此外,这种表达能力更强的GNN在测试集精度方面优于其他GNNs,并且在许多图分类benchmarks上实现了最先进的性能。
READOUT表示一个置换不变性函数(permutation invariant function),也可以是一个图级pooling函数。

上图是WL test的例子,请移步原博客看解释。
https://www.cnblogs.com/BlairGrowing/p/15961951.html


_______________________________________
一点题外话啊,读完回忆一下之前读的论文,觉得还有需要关注的疑问,后期会单独写一篇回答自己的疑问(如果能找到答案的话就贴回答)

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容





所有评论(0)