卡诺图最简化SOP/POS表达式
卡诺图最简化SOP/POS表达式一. 卡诺图(Karnaugh Map)二. 原理分析1. 化简SOP2. 化简POS一. 卡诺图(Karnaugh Map)通俗易懂的来讲,卡诺图是一种方格图,其行和列遵循固定的规则分布(对所有变量:相邻方格之间一定且仅改变一个变量的值)...
卡诺图最简化SOP/POS表达式及扩展
注:文章内容基于 Thomas L. Floyd-Digital Fundamentals-Prentice Hall (2014)
结合笔者学习经验给出最适分析思路和扩展方法
一. 卡诺图(Karnaugh Map)
通俗易懂的来讲,卡诺图是一种方格图,其行和列遵循固定的规则分布(对所有变量:相邻方格之间一定且仅改变一个变量的值)
- 标准卡诺图
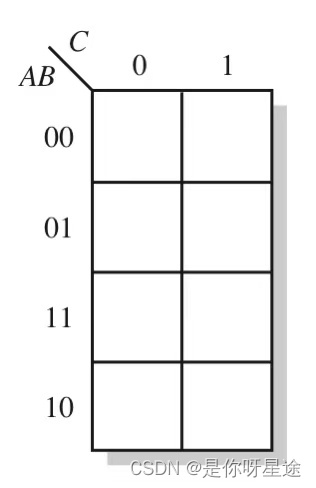

- 非标准卡诺图
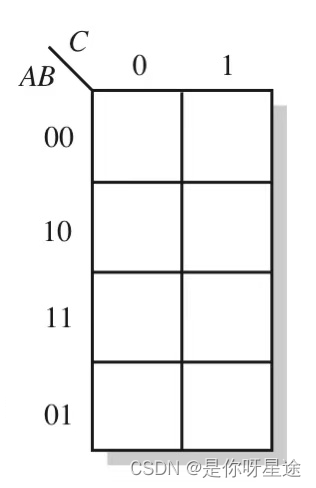
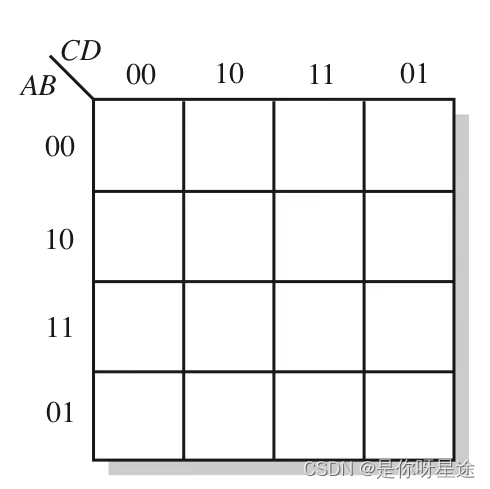
标准卡诺图与非标准卡诺图之间的区别:
(1). 标准卡诺图在满足分布规则的前提下遵循最低位变量进行0-1顺序变化
(2). 非标准卡诺图则非,但仍遵循卡诺图分布规则
实际上无论是标准或非标准卡诺图,在求解化简过程中结果是一样的
但写作标准式是避免化简出错的主要手段
卡诺图的行列显示了输入变量的所有可能情况,并在卡诺图中填入变量的实际输入情况,用以简化输入表达式
注:
卡诺图一般用于讨论3-4变量的输入情况
一般情况下,不超过5个变量
当超过5变量时,使用卡诺图化简表达式显得冗长复杂,则会使用其他方法化简,卡诺图化简提供了一种表达式化简的可视化思路
二. 原理分析
卡诺图最主要用于获取最小项表达式
也就是我们常说的化简表达式
常见用于简化逻辑函数的规范范式SOP/POS表达式
关于SOP/POS表达式的详见说明请参考:
逻辑函数规范范式——SOP/POS表达式
(1). 填入卡诺图
1如下给出填入卡诺图步骤
①. 先由给出SOP/POS表达式写出其标准式
②. 将对应SOP输出值置1/POS输出值置0,给出对应表达式的真值表
③. 将真值表对应填入卡诺图中
SOP/POS标准化方法参考如下详解:
SOP/POS标准化方法
当然,需要注意的是,如果刚开始给你的表达式并不复杂
即使对应四变量,也可以通过布尔代数公式将其化简至最简式
就没有必要再通过卡诺图复杂化化简过程了
(2). 通过卡诺图化简
1. 化简SOP(矩形框选法)
如下给出通过卡诺图化简步骤
①. 将SOP标准式对应真值表全部填入卡诺图中
(卡诺图对应位置填1,及卡诺图中显示为1的地方为对应输出值为1的所有可能情况)
(而对于某个方格内同时对应的四个变量作为输入,表示这种输入通过SOP表达式的输出为1)
②. 将卡诺图中的1依照矩形框取方法1逐一划分区域
③. 将划分区域写成表达式形式并相加写成SOP表达式
所得表达式即为最简/最小项SOP表达式
这里分析一下为什么使用矩形框取方法可以实现化简
- 首先化简的原理就是找
变化量,消去变化量(或者可以理解为变化量在输入输出过程中不起作用,也成为无关变量) - 每有一个矩形区域就构成
SOP表达式中的一项 - 为什么两个矩形区域之间不连接就不能化简?这就要根据卡诺图分布的原则来说明了
卡诺图分布原则保证了相邻区域之间有且只有一个变量的值发生改变,发生改变的变量即为无关变量
这表明无论该变量取0或是1,其输出值都为1,故为无关项
而当两区域不全相邻,即两区域不能构成一个矩形区域,在卡诺图中就无法找到两区域间的无关量,故不能将两项表达式化简成一项
(1). 三元卡诺图化简
以下图为例
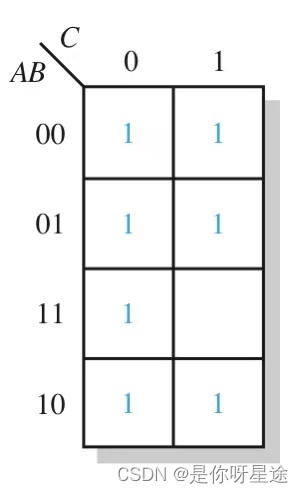
通过框选方法得到图
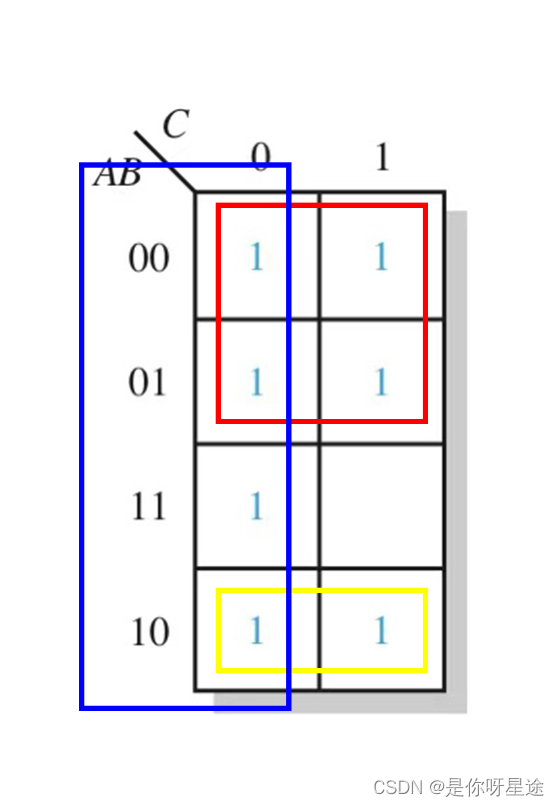
依据圈出矩形框来判断所圈矩形框的最小项表达式:
①. 观察所圈矩形框中“1”的个数,确定该矩形框对应最小项的变量个数
②. 根据不变量写出表达式
(1) 蓝色矩形框:框中“1”的个数为4,确定该项变量为1,找不变量,在这一过程中 C = 0 C=0 C=0保持不变,则将不变量作为该项式的变量—— C ‾ \overline{C} C(若不变量满足 C = 1 C=1 C=1保持不变,则该项式变量—— C C C)
(2) 红色矩形框:框中“1”的个数为4,确定该项变量为1,找不变量,在这一过程中 A = 0 A=0 A=0保持不变,则将不变量作为该项式的变量—— A ‾ \overline{A} A(若不变量满足 A = 1 A=1 A=1保持不变,则该项式变量—— A A A)
(3) 黄色矩形框:框中“1”的个数为2,确定该项变量为2,找不变量,在这一过程中 A B = 10 AB=10 AB=10保持不变,则将不变量作为该项式的变量—— A B ‾ A\overline{B} AB
(4) 三项相加得到最终表达式为 C ‾ \overline{C} C+ A ‾ \overline{A} A+ A B ‾ A\overline{B} AB
图中圈出三个矩形框,表示所得表达式中最小项式的个数为三,其中每一个矩形框代表一个最小项式
所圈出的矩形框包含“1”的个数与可消去变量或最小项项式变量的关系为
M i = N − log 2 m i M_{i}=N-\log_{2}{{m_{i}}} Mi=N−log2mi
定义:
N表示总变量数;
mi表示第i个矩形框内“1”的个数;
Mi表示第i个矩形框对应最小项的变量个数
(2). 四元卡诺图化简
对于三元卡诺图,由于三变量所能产生的最多情况个数为8种,不存在较为复杂的空间排布规律
但对于四元卡诺图,可能会出现较为复杂的空间排布规律,此情况下,框选的范围就不再只是狭义上的矩形框范围了,该定义扩展到物理范围上
通过如下图给出
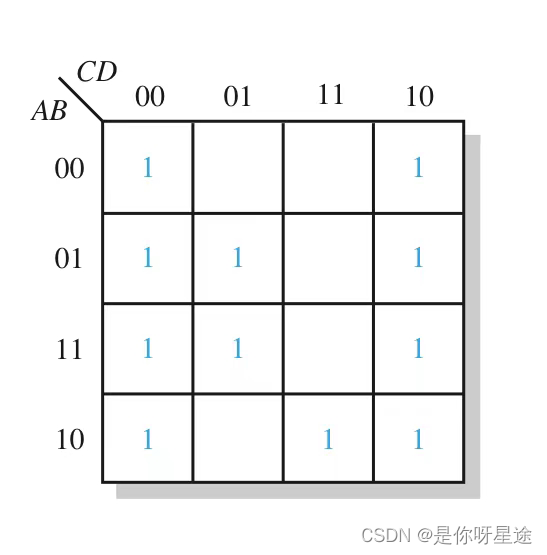
实际圈出过程为:
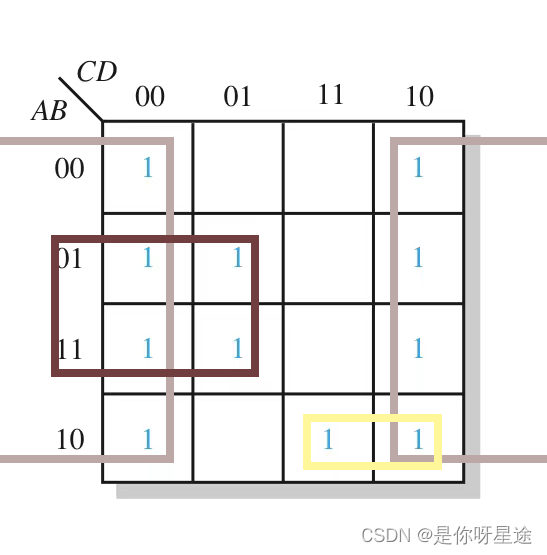
可以发现,左右两侧并不相邻的部分被圈入同一个矩形框种
对于这种情况,看似不相邻,实则是相邻的,因为左右两列始终满足相邻条件:两个方格之间只有一个变量发生改变,而对于左右两侧共四组每一组都满足相邻条件,实际上无论是上下两侧还是左右两侧,都满足相邻条件,即称之为物理相邻
可以使用镜像法来分析物理上的相邻,即可作如下图
(镜像法为个人证明所得方法,并不推荐使用于考试或程序设计当中)
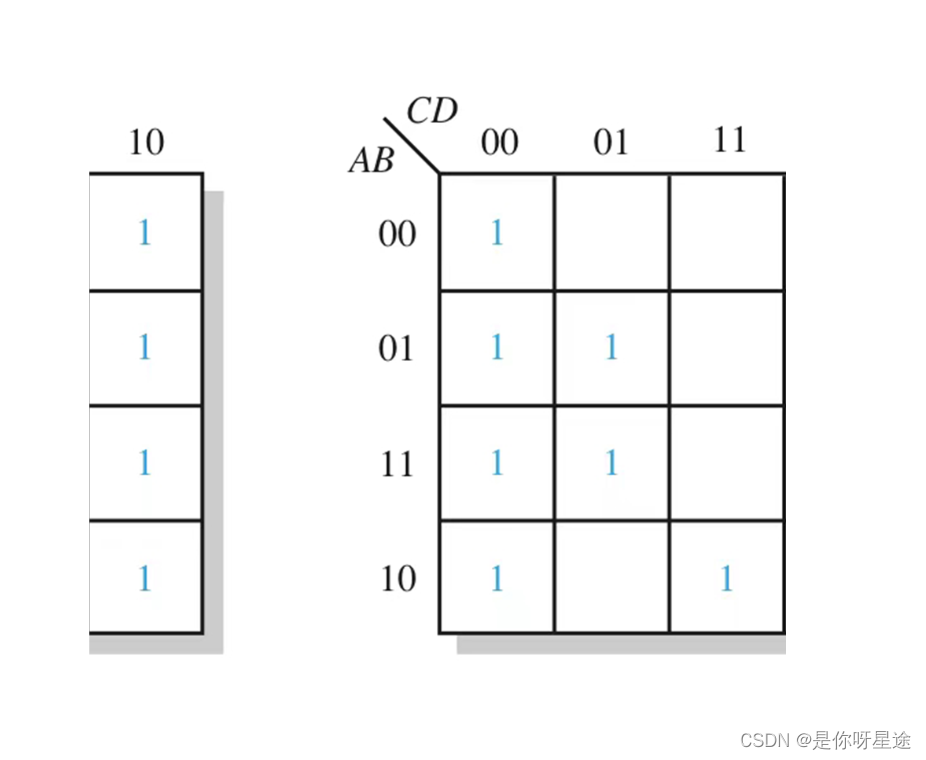
前面讲过,对于不规范的卡诺图,化简方式仍然成立且完全相同:标准/非标准卡诺图解析
所以,仍然使用前面的化简方法,对上图化简为
(1) 灰色矩形框:框中“1”的个数为8,确定该项变量为1,找不变量,在这一过程中 D = 0 D=0 D=0保持不变,则将不变量作为该项式的变量—— D ‾ \overline{D} D
(2) 棕色矩形框:框中“1”的个数为4,确定该项变量为2,找不变量,在这一过程中 B C = 10 BC=10 BC=10保持不变,则将不变量作为该项式的变量—— B C ‾ B\overline{C} BC
(3) 黄色矩形框:框中“1”的个数为2,确定该项变量为3,找不变量,在这一过程中 A B C = 101 ABC=101 ABC=101保持不变,则将不变量作为该项式的变量—— A B ‾ C A\overline{B}C ABC
(4) 三项相加得到最终表达式为 D ‾ \overline{D} D+ B C ‾ B\overline{C} BC+ A B ‾ C A\overline{B}C ABC
(3). 四元卡诺图化简常见错误情况
对较复杂卡诺图的化简可能会遇到的两种问题:
- 漏化简
- 化简方式始终是唯一的,因为化简遵循
最大选取原则,化简出现多种可能说明化简错误
给出如下卡诺图
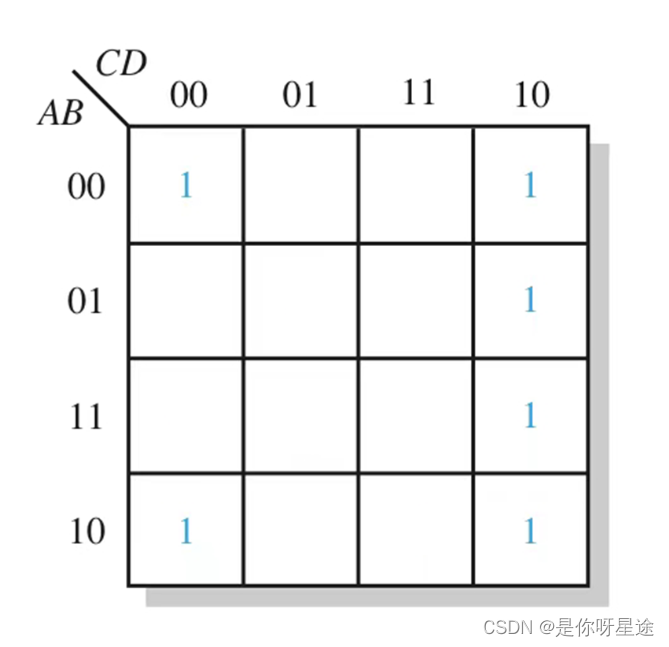
首先四角上的四个方格是成对相邻的,例如左上角0000分别与左下角1000和右上角0010相邻,同理对另外三个角也满足相邻条件,即此四角可以被圈入为一个矩形框
那么对于该卡诺图
化简方式应该为
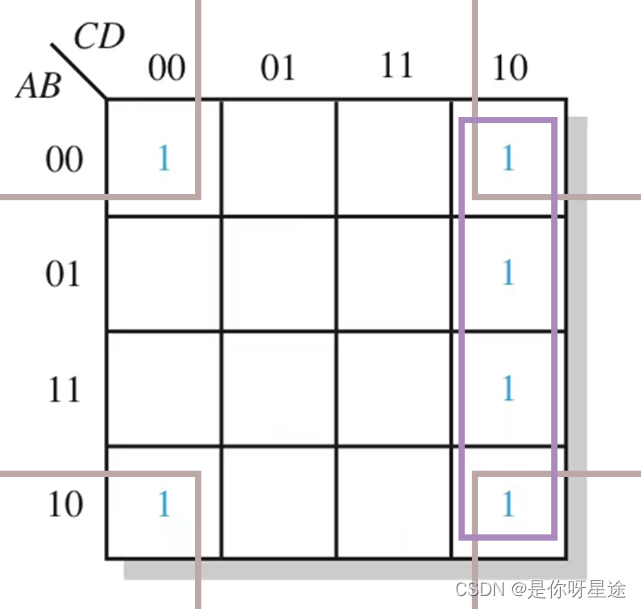
仍然依据上述化简方式
(1) 灰色矩形框:框中“1”的个数为4,确定该项变量为2,找不变量,在这一过程中 B D = 00 BD=00 BD=00保持不变,则将不变量作为该项式的变量—— B ‾ D ‾ \overline{B}\overline{D} BD
(2) 紫色矩形框:框中“1”的个数为4,确定该项变量为2,找不变量,在这一过程中 C D = 10 CD=10 CD=10保持不变,则将不变量作为该项式的变量—— C D ‾ C\overline{D} CD
(3) 两项相加得到最终表达式为 B ‾ D ‾ \overline{B}\overline{D} BD+ C D ‾ C\overline{D} CD
2. 化简POS
如下给出通过卡诺图化简步骤
①. 将POS标准式对应真值表全部填入卡诺图中
(卡诺图对应位置填0,及卡诺图中显示为0的地方为对应输出值为0的所有可能情况)
(而对于某个方格内同时对应的四个变量作为输入,表示这种输入通过POS表达式的输出为0)
②. 将卡诺图中的0依照矩形框取方法1逐一划分区域
③. 将划分区域写成表达式形式并相乘写成POS表达式
所得表达式即为最简/最小项POS表达式
实际上,其方法与SOP表达式化简的方式完全一致,唯一区别在于表达式的化简原理略有不同,区别在用于确定不同表达式的唯一输入输出值
故,对应于POS表达式的卡诺图,需要将对应表达式所在卡诺图位置置0,并依据给出唯一输入真值为0给出最小项表达式
以下图为例
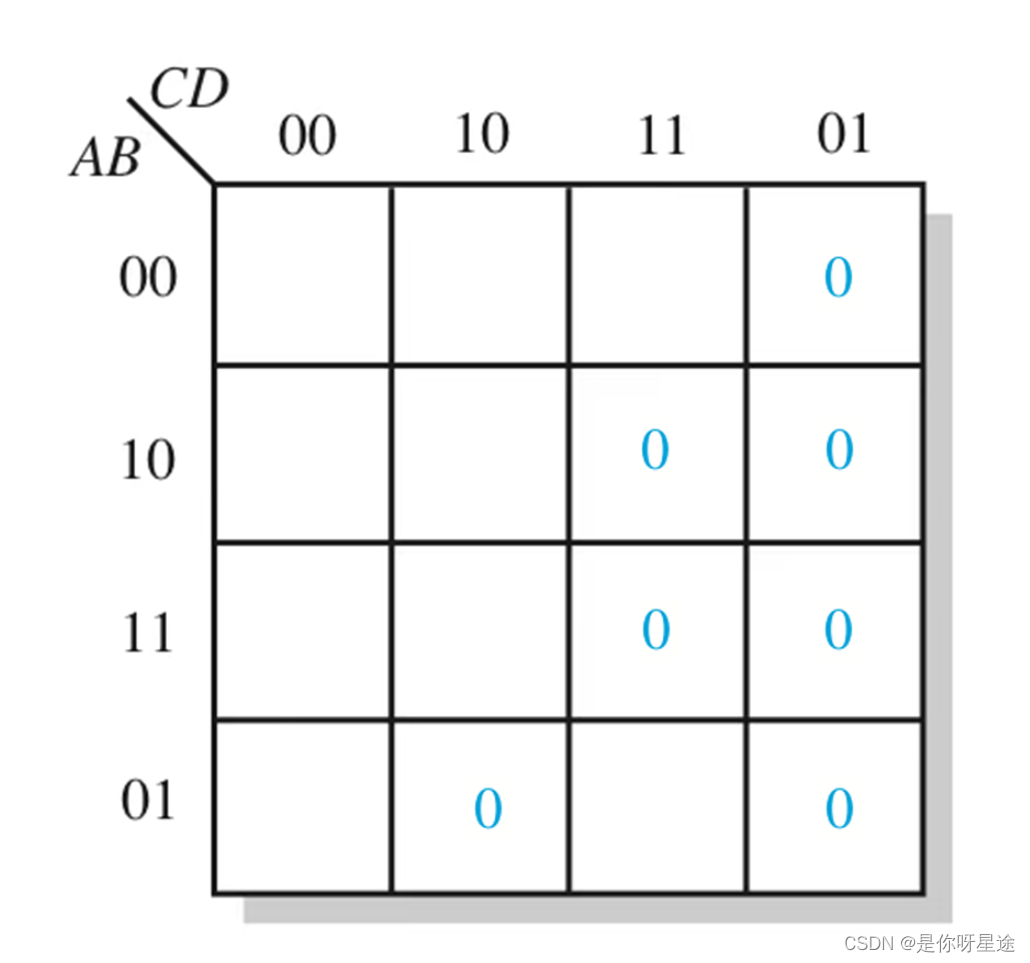
经矩形框选得到:
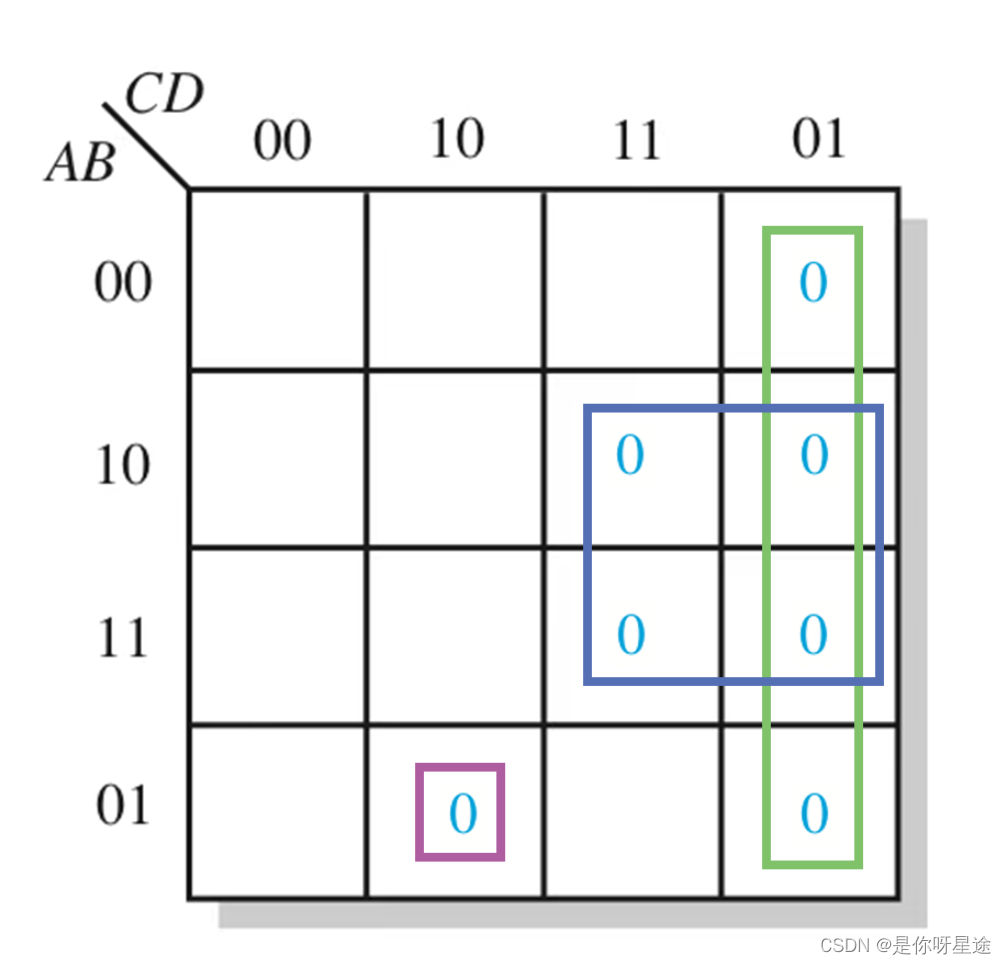
分析给出其POS对应的最小项表达式:
(1) 绿色矩形框:框中“1”的个数为4,确定该项变量为2,找不变量,在这一过程中 C D = 01 CD=01 CD=01保持不变,则将不变量作为该项式的变量—— C + D ‾ C+\overline{D} C+D(若不变量满足 C = 0 C=0 C=0保持不变,则该项式变量—— C C C/若不变量满足 C = 1 C=1 C=1保持不变,则该项式变量—— C ‾ \overline{C} C,这一原则是根据SOP/POS标准化过程给出的)
(2) 深蓝色矩形框:框中“1”的个数为4,确定该项变量为2,找不变量,在这一过程中 A D = 11 AD=11 AD=11保持不变,则将不变量作为该项式的变量—— A ‾ + D ‾ \overline{A}+\overline{D} A+D
(3) 玫瑰色矩形框:框中“1”的个数为1,确定该项变量为4,找不变量,在这一过程中 A B C D = 0110 ABCD=0110 ABCD=0110保持不变,则将不变量作为该项式的变量—— A + B ‾ + C ‾ + D A+\overline{B}+\overline{C}+D A+B+C+D
(4) 三项相乘得到最终表达式为( C + D ‾ C+\overline{D} C+D)( A ‾ + D ‾ \overline{A}+\overline{D} A+D)( A + B ‾ + C ‾ + D A+\overline{B}+\overline{C}+D A+B+C+D)
3. 由SOP/POS表达式得到POS/SOP最小项表达式
和真值表对应互补关系一样:
SOP/POS相互转化
卡诺图也有着“非1即0”的互补关系:
通过SOP/POS给出的表达式对应卡诺图中全部的1/0之外的全部空余区域,全部为给出表达式置位的补码
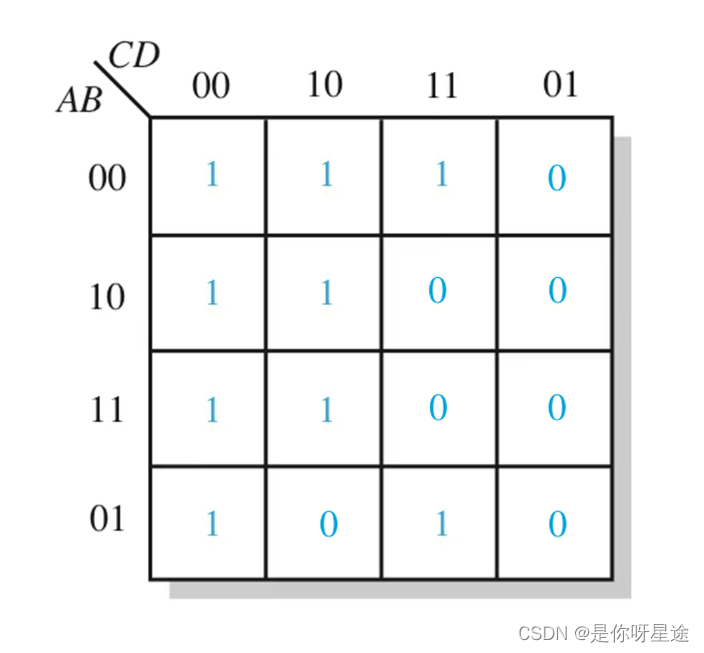
并根据给出的全卡诺图求需要的最小项式即可
希望能够帮到迷途之中的你,知识有限,如有学术错误请及时指正,感谢大家的阅读
(^^)/▽ ▽\(^^)

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容





所有评论(0)