数字图像处理,经典对比度增强算法
直方图均衡化的英文名称是Histogram Equalization. 图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。直方图拉伸是通过对比度拉伸对直方图进行调整,从而“扩大”前景和背景灰度的差别,以达到增强对比度的目的,这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数
关于图像增强必须清楚的基本概念
1.图像增强的目的:
1)改善图像的视觉效果,
2)转换为更适合于人或机器分析处理的形式
3)突出对人或机器分析有意义的信息
4)抑制无用信息,提高图像的使用价值
5)增强后的图像并不一定保真
2,图像增强的方法分类:
1)从处理对象分类:灰度图像,(伪)彩色图像
2)从处理策略分类:全局处理,局部处理(ROI ROI,Region of Interest Interest)
3)从处理方法分类:空间域(点域运算,即灰度变换;邻域方法,即空域滤波),频域方法
4)从处理目的分类:图像锐化,平滑去噪,灰度调整(对比度增强)
3,图像增强的方法之对比度增强
1)灰度变换法
线性变换(已实现)
对数变换(已实现)
指数变换(已实现)
2)直方图调整法
直方图均衡化(已实现)
直方图匹配(未实现)
一,直方图均衡化
直方图均衡化的英文名称是Histogram Equalization.
图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。直方图拉伸是通过对比度拉伸对直方图进行调整,从而“扩大”前景和背景灰度的差别,以达到增强对比度的目的,这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。
缺点:
1)变换后图像的灰度级减少,某些细节消失;
2)某些图像,如直方图有高峰,经处理后对比度不自然的过分增强。
直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。
这种方法通常用来增加许多图像的局部对比度,尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法,亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度,直方图均衡化通过有效地扩展常用的亮度来实现这种功能。
这种方法对于背景和前景都太亮或者太暗的图像非常有用,这种方法尤其是可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。这种方法的一个主要优势是它是一个相当直观的技术并且是可逆操作,如果已知均衡化函数,那么就可以恢复原始的直方图,并且计算量也不大。这种方法的一个缺点是它对处理的数据不加选择,它可能会增加背景杂讯的对比度并且降低有用信号的对比度。

关于编程实现,同样是不调用matlab库函数,自己编程实现。这样可以更深刻地理解直方图均衡化技术,提高编程能力。
实现代码(matlab):
clc;
close all;
clear all;
src_img = imread('flyman_gray.bmp');
figure (1)
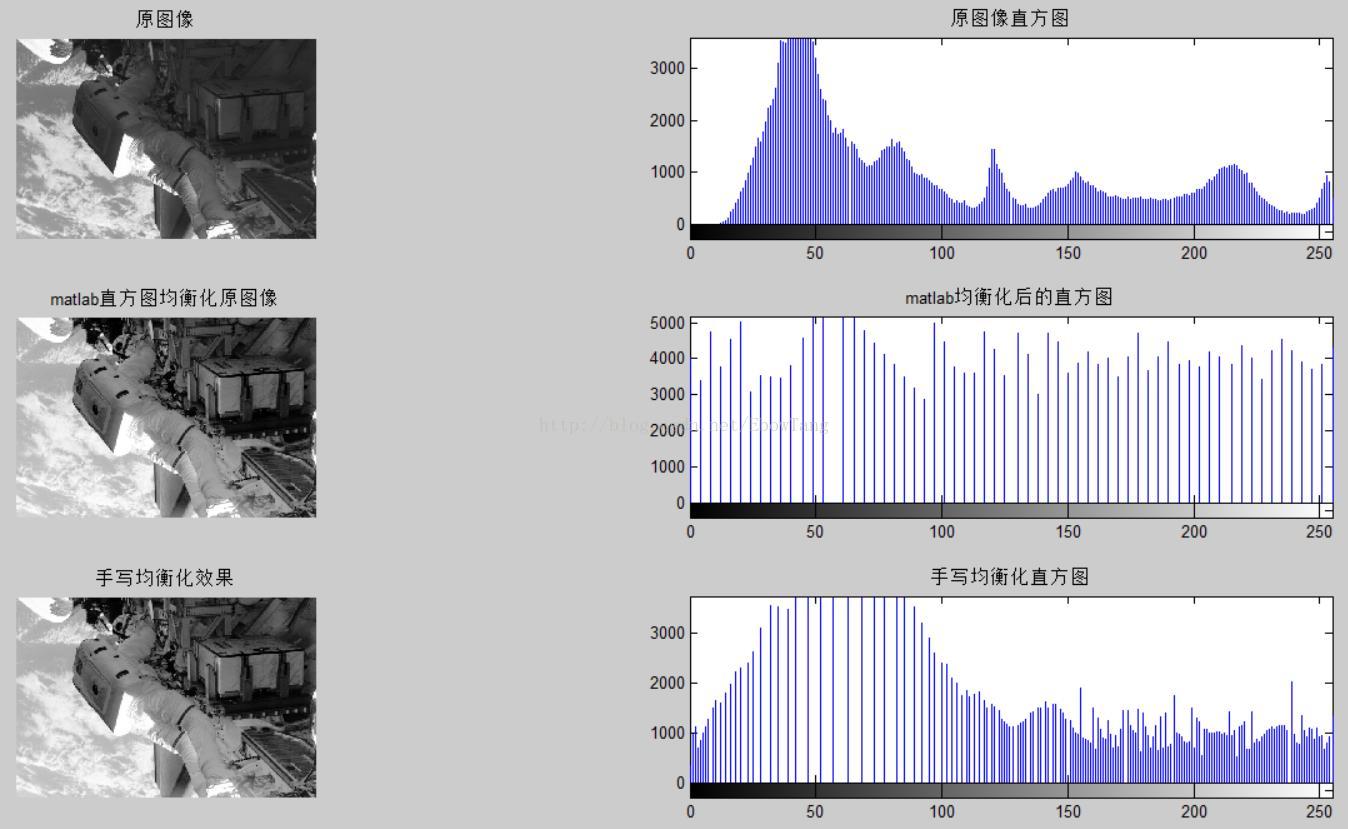
subplot(321),imshow(src_img),title('原图像');%显示原始图像
subplot(322),imhist(src_img),title('原图像直方图');%显示原始图像直方图
matlab_eq=histeq(src_img); %利用matlab的函数直方图均衡化
subplot(323),imshow(matlab_eq),title('matlab直方图均衡化原图像');%显示原始图像
subplot(324),imhist(matlab_eq),title('matlab均衡化后的直方图');%显示原始图像直方图
dst_img=myHE(src_img); %利用自己写的函数直方图均衡化
subplot(325),imshow(dst_img),title('手写均衡化效果');%显示原始图像
subplot(326),imhist(dst_img),title('手写均衡化直方图');%显示原始图像直方图 直方图均衡化函数的实现:
function dst_img=myHE(src_img)
[height,width] = size(src_img);
dst_img=uint8(zeros(height,width));
%进行像素灰度统计;
NumPixel = zeros(1,256);%统计各灰度数目,共256个灰度级
for i = 1:height
for j = 1: width
NumPixel(src_img(i,j) + 1) = NumPixel(src_img(i,j) + 1) + 1;%对应灰度值像素点数量增加一
end
end
%计算灰度分布密度
ProbPixel = zeros(1,256);
for i = 1:256
ProbPixel(i) = NumPixel(i) / (height * width * 1.0);
end
%计算累计直方图分布
CumuPixel = zeros(1,256);
for i = 1:256
if i == 1
CumuPixel(i) = ProbPixel(i);
else
CumuPixel(i) = CumuPixel(i - 1) + ProbPixel(i);
end
end
% 指定范围进行均衡化
% pixel_max=max(max(I));
% pixel_min=min(min(I));
pixel_max=255;
pixel_min=0;
%对灰度值进行映射(均衡化)
for i = 1:height
for j = 1: width
dst_img(i,j) = CumuPixel(src_img(i,j)+1)*(pixel_max-pixel_min)+pixel_min;
end
end
return;
为什们和matlab的直方图不一样呢???
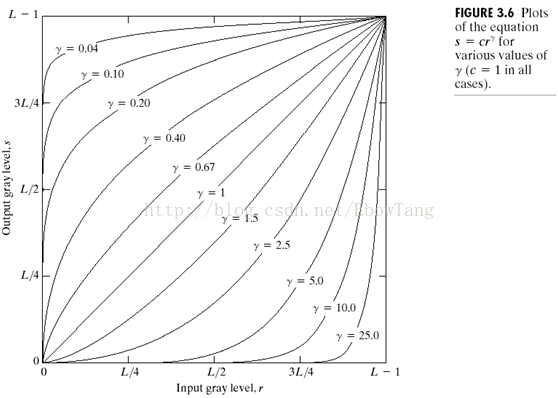
二,指数变换
clc;
close all;
clear all;
% -------------Gamma Transformations-----------------
%f = imread('Fig0316(4)(bottom_left).tif');
f = imread('seed.tif');
Gamma = 0.4;
g2 = myExpEnhance(f,Gamma);
figure();
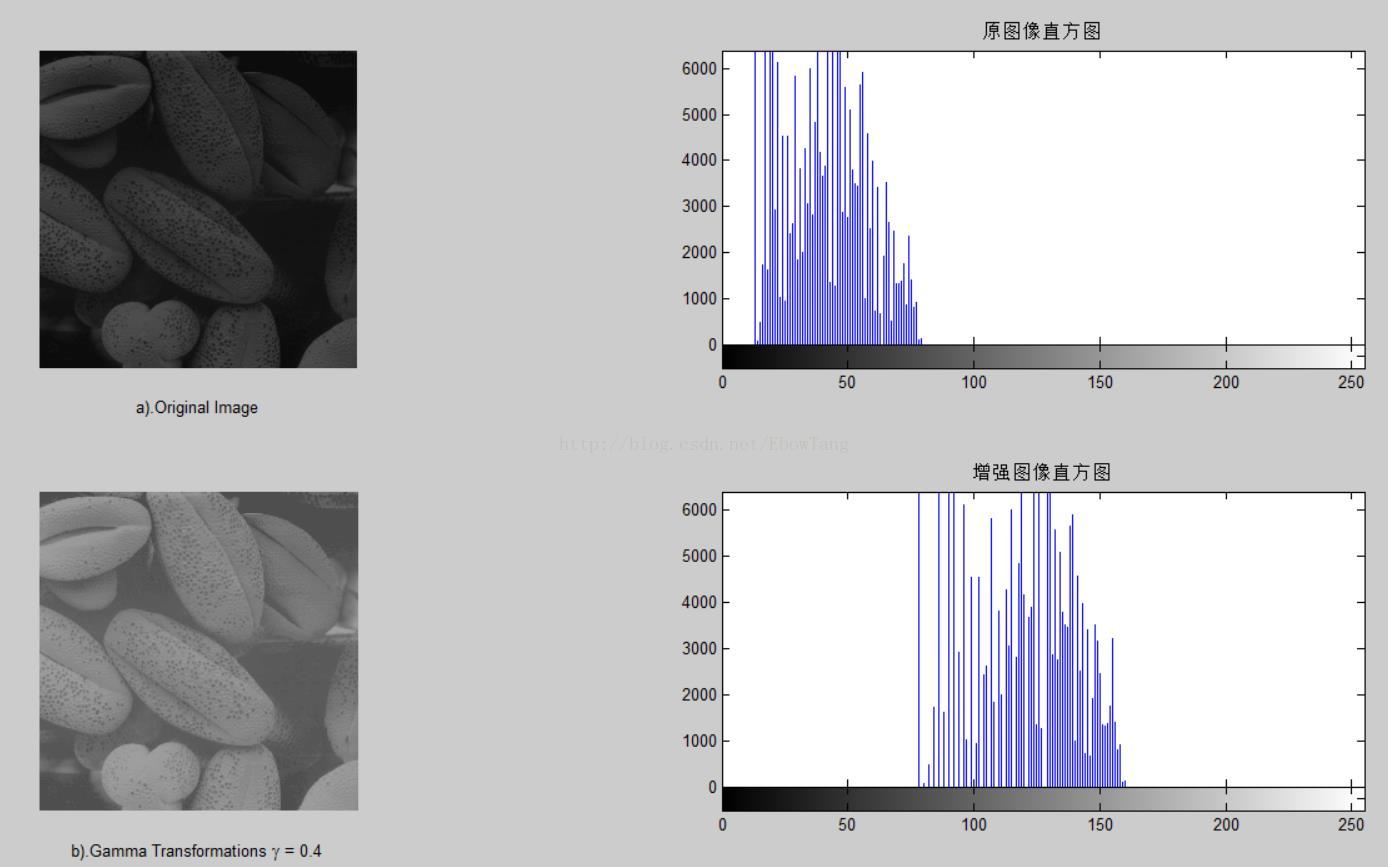
subplot(221); imshow(f); xlabel('a).Original Image');
subplot(222),imhist(f),title('原图像直方图');%显示原始图像直方图
subplot(223); imshow(g2); xlabel('b).Gamma Transformations \gamma = 0.4');
subplot(224),imhist(g2),title('增强图像直方图');%显示原始图像直方图 function dst_img=myExpEnhance(src_img,Gamma)
src_img = mat2gray(src_img,[0 255]);%将图像矩阵A中介于amin和amax的数据归一化处理, 其余小于amin的元素都变为0, 大于amax的元素都变为1。
C = 1;
g2 = C*(src_img.^Gamma);
%反归一化
max=255;
min=0;
dst_img=uint8(g2*(max-min)+min);三,对数变换
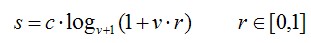

clc;
close all;
clear all;
%-------------Log Transformations-----------------
f = imread('seed.tif');
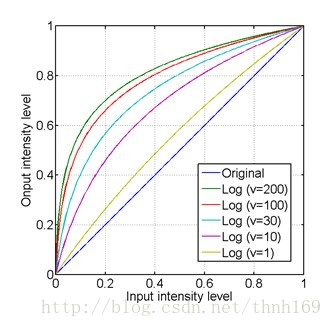
g_1 = myLogEnhance(f,10);
g_2 = myLogEnhance(f,100);
g_3 = myLogEnhance(f,200);
figure();
subplot(2,2,1);
imshow(f);xlabel('a).Original Image');
subplot(2,2,2);
imshow(g_1);xlabel('b).Log Transformations v=10');
subplot(2,2,3);
imshow(g_2);xlabel('c).Log Transformations v=100');
subplot(2,2,4);
imshow(g_3);
xlabel('d).Log Transformations v=200');对数变换核心函数
function dst_img=myLogEnhance(src_img,v)
c=1.0;
src_img = mat2gray(src_img,[0 255]);
g =c*log2(1 + v*src_img)/log2(v+1);
%反归一化
max=255;
min=0;
dst_img=uint8(g*(max-min)+min);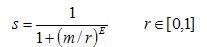
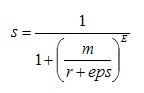
 。输出范围大致为【0-1】,为了精确起见,使用mat2gray函数将其归一化到精确的[0-1]。调用格式如下。
。输出范围大致为【0-1】,为了精确起见,使用mat2gray函数将其归一化到精确的[0-1]。调用格式如下。
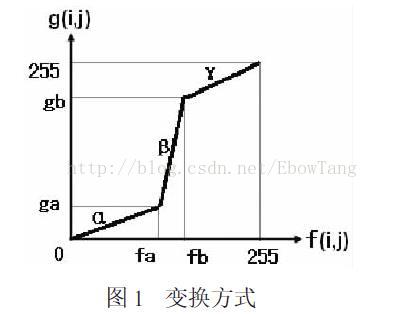
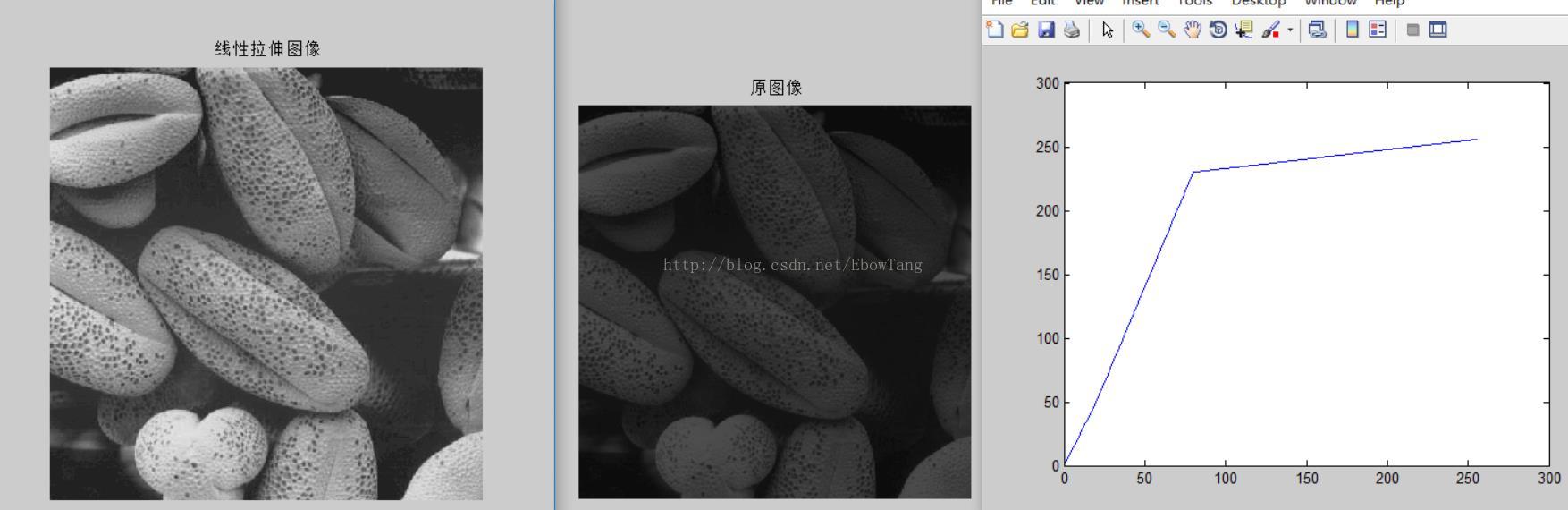
五,线性拉伸
clc;
close all;
clear all;
I=imread('seed.tif');
[m,n,k]=size(I);
figure (1)
imshow('seed.tif');title(' 原图像');
mid=mean(mean(I));
%横轴
fa=20; fb=80;
%纵轴
ga=50; gb=230;
J=myLinearEnhance(I,fa,fb,ga,gb);
figure (2)
imshow(J);title(' 线性拉伸图像');
pixel_f=1:256;
pixel_g=zeros(1,256);
%三段斜率,小于1表示该段将会被收缩
k1=double(ga/fa);
k2=(gb- ga)/(fb- fa);
k3=(256- gb)/(256- fb);
for i=1:256
if i <= fa
pixel_g(i)= k1*i;
elseif fa < i && i <= fb
pixel_g(i)= k2*( i- fa)+ ga;
else
pixel_g(i)= k3*( i - fb)+ gb;
end
end
figure (3)
plot(pixel_f,pixel_g);function dst_img=myLinearEnhance(src_img,fa,fb,ga,gb)
[height,width] = size(src_img);
dst_img=uint8(zeros(height,width));
src_img=double(src_img);
%三段斜率
k1=ga/fa;
k2=(gb- ga)/(fb- fa);
k3=(255- gb)/(255- fb);
for i=1:height
for j=1:width
if src_img(i,j) <= fa
dst_img(i,j)= k1*src_img(i,j);
elseif fa < src_img(i,j) && src_img(i,j) <= fb
dst_img(i,j)= k2*( src_img(i,j)- fa)+ ga;
else
dst_img(i,j)= k3*( src_img(i,j)- fb)+ gb;
end
end
end
dst_img=uint8(dst_img); 附录:
附录网上的另一份讲解:
直方图均衡化算法分为三个步骤,第一步是统计直方图每个灰度级出现的次数,第二步是累计归一化的直方图,第三步是计算新的像素值。
第一步:
for(i=0;i<height;i++)
for(j=0;j<width;j++)
n[s[i][j]]++;
for(i=0;i<L;i++)
p[i]=n[i]/(width*height);
这里,n[i]表示的是灰度级为i的像素的个数,L表示的是最大灰度级,width和height分别表示的是原始图像的宽度和高度,所以,p[i]表示的就是灰度级为i的像素在整幅图像中出现的概率(其实就是p[]这个数组存储的就是这幅图像的归一化之后的直方图)。
第二步:
for(i=0;i<=L;i++)
for(j=0;j<=i;j++)
c[i]+=p[j];
c[]这个数组存储的就是累计的归一化直方图。
第三步:
max=min=s[0][0];
for(i=0;i<height;i++)
for(j=0;j<width;j++)
if(max<s[i][j]){
max=s[i][j];
}else if(min>s[i][j]){
min=s[i][j];
}
找出像素的最大值和最小值。
for(i=0;i<height;i++)
for(j=0;j<width;j++)
t[i][j]=c[s[i][j]]*(max-min)+min;
t[][]就是最终直方图均衡化之后的结果。
收录优秀代码:
这份代码写得不错,学习了,原博客地址见参考资源【3】!
#include <stdio.h>
#include <iostream>
#include "fftw3.h"
#include "string"
#include "vector"
#include <windows.h>
#include <opencv2/legacy/legacy.hpp>
#include <opencv2/nonfree/nonfree.hpp>//opencv_nonfree模块:包含一些拥有专利的算法,如SIFT、SURF函数源码。
#include "opencv2/core/core.hpp"
#include "opencv2/features2d/features2d.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <opencv2/nonfree/features2d.hpp>
using namespace cv;
using namespace std;
class hisEqt
{
public:
hisEqt::hisEqt();
hisEqt::~hisEqt();
public:
int w;
int h;
int nlen;
int *pHis;
float *pdf;
//=====求像素分布概率密度====
void getPdf();
//======统计像素个数=======
void getHis(unsigned char*imgdata);
//==========画统计分布直方图===============
void drawHistogram(const float*pdf,Mat &hist1);
//===========直方图均衡化==========
void hisBal();
//====直方图均衡化后的图像===
void imgBal(unsigned char* img);
};
hisEqt::hisEqt() :nlen(0){
pHis = new int[256 * sizeof(int)];
memset(pHis, 0, 256 * sizeof(int));
pdf = new float[255 * sizeof(float)];
memset(pdf, 0, 255 * sizeof(float));
}
hisEqt::~hisEqt(){
delete[]pHis;
delete[]pdf;
}
//======统计像素个数=======
void hisEqt::getHis(unsigned char*imgdata){
for (int i = 0; i<nlen; i++)
{
pHis[imgdata[i]]++;
}
}
//=====求像素分布概率密度====
void hisEqt::getPdf(){
for (int k = 0; k<256; k++)
{
pdf[k] = pHis[k] / float(nlen);
}
}
//===========直方图均衡化==========
void hisEqt::hisBal(){
for (int k = 1; k<256; k++)
{
pdf[k] += pdf[k - 1];
}
for (int k = 0; k<256; k++)
{
pHis[k] = 255 * pdf[k];
}
}
//====直方图均衡化
void hisEqt::imgBal(unsigned char* img){
for (int i = 0; i<nlen; i++)
{
img[i] = pHis[img[i]];
}
}
void hisEqt::drawHistogram(const float *pdf, Mat& hist1){
for (int k = 0; k<256; k++)
{
if (k % 2 == 0)
{
Point a(k, 255), b(k, 255 - pdf[k] * 2550);
line(hist1,
a,
b,
Scalar(0, 0, 255),
1);
}
else
{
Point a(k, 255), b(k, 255 - pdf[k] * 2550);
line(hist1,
a,
b,
Scalar(0, 255, 0),
1);
}
}
}
int main()
{
Mat image = imread("Fig0651(a)(flower_no_compression).tif");
if (!image.data)
return -1;
Mat hist2(256, 256, CV_8UC3, Scalar(0, 0, 0));
Mat hist1(256, 256, CV_8UC3, Scalar(0, 0, 0));
Mat imgOut = Mat(image.rows, image.cols, CV_8UC3, Scalar(0, 0, 0));
vector<Mat> planes;
int chn = image.channels();
if (chn == 3)
{
split(image, planes);
}
while (chn)
{
chn--;
unsigned char* imageData = new unsigned char[sizeof(unsigned char)*(image.cols*image.rows)];
memcpy(imageData, planes[chn].data, planes[chn].cols*planes[chn].rows);
hisEqt his;//自定义的类
his.nlen = image.rows*image.cols;
his.getHis(imageData);
his.getPdf();
// //======画原图直方图并保存============
his.drawHistogram(his.pdf, hist1);
string pic_name = "hisline";
pic_name = pic_name + to_string(chn);
pic_name=pic_name+ ".jpg";
imwrite(pic_name, hist1);
his.hisBal();
his.getPdf();
// //======画均衡化后直方图并保存============
his.drawHistogram(his.pdf, hist2);
string pic_name0 = "his_balanceline";
pic_name0 = pic_name0 + to_string(chn);
pic_name0 = pic_name0 + ".jpg";
imwrite(pic_name0, hist2);
// //=====图像均衡化===
his.imgBal(imageData);
memcpy(planes[chn].data, imageData, planes[chn].cols*planes[chn].rows);
delete[] imageData;
imageData = NULL;
}
merge(planes, imgOut);//单通道合并
imwrite("result.jpg", imgOut);
return 0;
}
参考资源
【1】http://blog.csdn.net/xiajun07061225/article/details/6910129
【2】数字图像处理,冈萨雷斯著
【3】http://blog.csdn.net/bettyshasha/article/details/46940805
【4】http://blog.csdn.net/terryzero/article/details/6043821
【5】http://www.myexception.cn/image/1450848.html

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容





所有评论(0)