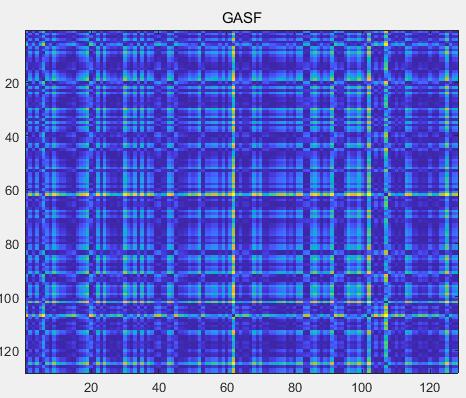
【信号转换】基于格拉姆矩阵(GASF/GADF)的一维信号转换图像算法【附MATLAB代码】
在转化后的二维图像中,同样出现了三个交叉特征,波峰较小的颜色也更浅,从左上角到右下角与加速度时程波形一一对应,说明经过GAF编码技术转化后,二维图像中的相应位置处以点、线、颜色等不同的特征形式对加速度时间序列进行了完整映 射。②极坐标相较 于直角坐标系,保持了绝对的时间相关性,不同间隔的时间序列经过重新缩放 并转化为极坐标,也会包含着不同的角度界限,这也为加速度一维时间序列在 转化成二维图像数据时
文章来源:微信公众号:EW Frontier
一.基于GAF的一维信号转换图像算法
1.1基本概念
GAF是利用坐标变化和格拉姆矩阵,实现将时间序列变化成为二维图像的 一种图像编码技术。GAF是采用极坐标系表示时间矩阵的,再用格拉姆矩阵对
生成的角度进行变换,这主要是因为格拉姆矩阵能够保持时间的依赖性,但是 并不能很好的区分有价值信息和高斯噪声,所以要先进行一次空间转换,最常 用的便是将笛卡尔坐标系转换成为极坐标系。
笛卡尔坐标系包括直角坐标系和斜角坐标系,两条数轴相交于原点,构成 了平面仿射坐标系,而且两数轴的度量单位一致。当两坐标轴垂直的时候就被 称为直角坐标系,否则就是斜角坐标系。提取的加速度数据一般都为二维直角 坐标系下的数据,每一个点的位置都由两个数字决定。而极坐标系也属于二维 坐标系,是指在平面取一点作为极点,并引出一个轴作为极轴,并确定单位长度与角度的正方向(一般取逆时针为正)。极坐标上的点位置都是由距离原点的距离以及和极轴的角度表示。因此笛卡尔坐标系的点可以与极坐标一一对应。
格拉姆矩阵可以计算一组向量的线性相关关系,常用于线性代数和几何中。一组n个向量的格拉姆矩阵是由一对对向量的点积组成的矩阵,如式(1)所示:

如果向量u和v的范数都为1,那么两个向量的点积可以改写为:
![]()
由此可知,如果处理的是单位向量,那么它们之间的点积只由角度所决定,这个角度可以用弧度表示,且计算出来的值将在-1和1之间。假设处理都是单 位向量,那么格拉姆矩阵将变为式(3):

式中,θi,j为两个向量之间的夹角。
1.2实现方法
斜拉索的加速度响应是典型的一维时间序列,通常在直角坐标系下,其横轴表示时间,纵坐标则代表了每一个时间点所对应的加速度的大小,单位是m/s2。
通过GAF将加速度响应转换为图形数据,实现过程如下:
步骤一,假定传感器采集加速度数据为X={x1,x2,x3,……,xn-1,xn},首 先通过式(4)进行归一化处理,并且将其缩放到[-1,1]之间。

步骤二,将步骤一中缩放后的加速度时间序列转换成为极坐标。主要注意 两个变量:加速度的值及其对应的时间戳。这两个变量可以分别用极坐标的角 度和半径来表示。在极坐标上进行编码,将缩放之后的加速度值用角余弦进行编码,值在[0,π]之间。将其对应的时间戳编码成为半径,公式如下所示:

式中,it—— i x对应的时间戳;M——归一化因子。
将区间[0,1]分成若干份,然后将0舍弃把剩余的点与时间序列数据关联起来,并且让每一个点都落到极坐标中的一个单位圆之中。当时间增加时,加速度时间序列也会以不同的角度和半径在这个单位圆之内不断的扭曲,如图1所示:

图1极坐标编码示意图
这样编码的优异性体现在:①整个编码都是双射的,即给定一段时间序列, 通过此种方式进行编码,得到的在极坐标下的结果将是唯一的。②极坐标相较 于直角坐标系,保持了绝对的时间相关性,不同间隔的时间序列经过重新缩放 并转化为极坐标,也会包含着不同的角度界限,这也为加速度一维时间序列在 转化成二维图像数据时提供了不同的信息粒度。
步骤三,加速度时间序列经过步骤二的极坐标变换,使其也蕴含了时间信
息,因此可以利用GAF对加速度时间序列进行重构。基于不同的算式可以生成 两种不同的图像,分别是格拉姆角和场(GASF)和格拉姆角差场(GADF),其表达 式分别为式(6)和式(7)。

由两个公式可知,随着时间的增加,编码的位置从矩阵的左上角一直运动
到右下角,所以时间维度就通过GAF编码到了矩阵的几何结构当中去。为了进 一步解释GAF编码过程,以图4-2为例进行说明。在加速度时间序列的波形中存在着三个较为明显的波峰,其中第一个波峰要小于后两者。在转化后的二维图像中,同样出现了三个交叉特征,波峰较小的颜色也更浅,从左上角到右下角与加速度时程波形一一对应,说明经过GAF编码技术转化后,二维图像中的相应位置处以点、线、颜色等不同的特征形式对加速度时间序列进行了完整映 射。

图2 GAF映射说明
二.MATLAB代码
本代码需要各位自行设置输入信号a,带入下列程序即可运行,本文的GASF与GDSF图像是利用BPSK调制信号生成。
load BPSK_SNR=0dB.mat% load BPSK_SNR=0dB.mati=1a=squeeze(data(i,1,:))+squeeze(data(i,2,:))*1j;%% GASF GADF%% 生成数据X = real(a');X = (X - min(X)) / (max(X) - min(X));m = length(X);%% 数据处理% 将数据归一化[1,-1]X = ((X - max(X)) + (X - min(X)))/(max(X) + min(X));% 求极坐标fai = acos(X);% 生成GASF = X' * X - sqrt(1 - X.^2)' * sqrt(1 - X.^2);GADF = sqrt(1-X.^2)' * X + X' * sqrt(1 - X.^2);%% 显示图(热力图)%im_1 = figure(1);imagesc(GASF)title('GASF')% saveas(im_1, 'GASF_2.bmp');%im_2 = figure(2);imagesc(GADF)title('GADF');% saveas(im_2, 'GADF_2.bmp');
三.仿真结果



开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献10条内容
已为社区贡献10条内容





所有评论(0)