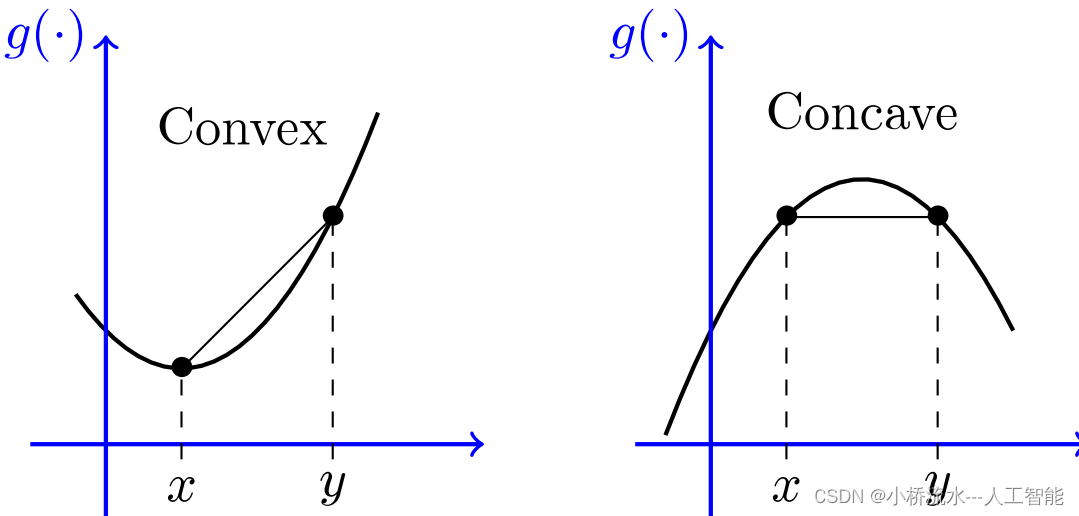
凹函数与凸函数Concave and convex functions
凸函数之所以呈现凹状,与我们主观常识不太一样,是因为凸凹性的定义是基于函数在任意两点之间的线段与函数图像之间的位置关系。具体来说,如果一个函数在任意两点之间的线段都在函数图像之上,则该函数被称为凸函数;如果线段都在函数图像之下,则该函数被称为凹函数。这个定义与我们日常生活中的直观感受可能不太一致,因为我们通常是根据一个物体或形状的表面来判断它是凸还是凹的。例如,一个凸起的山丘或球面通常被认为是凸的

凹函数与凸函数Concave and convex functions
1. 凸函数的基本概念
凸函数是一类特殊的数学函数,其由来可以追溯到丹麦数学家约翰・詹森(Jensen)和爱因斯坦在瑞士的数学老师闵科夫斯基。凸函数的基本定义是:在实数域或复数域上的向量空间中,如果对于定义域内的任意两个向量x和y,以及任意实数α(0 ≤ α ≤ 1),都有f(αx + (1 - α)y) ≤ αf(x) + (1 - α)f(y),则称f为凸函数。这个定义也可以用二阶导数来理解,即如果一个函数的二阶导数在定义域内非负,那么这个函数就是凸函数。
凸函数的一个重要特性是,函数的任意两点之间的线段都在函数图像之上,即函数图像呈现出一种“向上凸”的形状。因此,凸函数也被称为上凸函数。相反,如果函数的任意两点之间的线段都在函数图像之下,即函数图像呈现出一种“向下凸”的形状,那么这个函数就被称为凹函数。
2. 凸函数的数学公式
凸函数的数学公式是:对于定义域内的任意两个向量x和y,以及任意实数α(0 ≤ α ≤ 1),都有 f ( α x + ( 1 − α ) y ) ≤ α f ( x ) + ( 1 − α ) f ( y ) f(αx + (1 - α)y) ≤ αf(x) + (1 - α)f(y) f(αx+(1−α)y)≤αf(x)+(1−α)f(y)。这个公式也可以用二阶导数来理解,即如果一个函数的二阶导数在定义域内非负,那么这个函数就是凸函数。
在凸函数中,任意两点之间的线段都在函数图像之上,即函数图像呈现出一种“向上凸”的形状。这个特性可以通过上述公式进行证明。假设x和y是定义域内的任意两个点,α是任意实数且满足0 ≤ α ≤ 1,那么αx + (1 - α)y就是x和y之间的一个点。根据凸函数的定义,我们有 f ( α x + ( 1 − α ) y ) ≤ α f ( x ) + ( 1 − α ) f ( y ) f(αx + (1 - α)y) ≤ αf(x) + (1 - α)f(y) f(αx+(1−α)y)≤αf(x)+(1−α)f(y),这意味着函数在点αx + (1 - α)y的函数值小于等于x和y处函数值的加权平均。因此,从图像上看,线段连接x和y上的点,其上的任意一点的函数值都大于等于该点对应的函数值,即函数图像在x和y之间的线段之上。
3.凸函数在机器学习上的应用
在机器学习中,凸函数具有非常重要的应用价值。这是因为许多机器学习问题都可以转化为优化问题,而凸函数在优化问题中具有很好的性质。例如,凸函数的局部最小值就是全局最小值,这意味着在求解优化问题时,我们不需要考虑函数的局部最小值,只需要找到全局最小值即可。此外,凸函数的优化问题通常具有较为简单的拓扑结构,可以通过一些简单的算法来求解,如梯度下降法、牛顿法等。
因此,在机器学习中,我们常常希望将问题转化为凸优化问题来求解。例如,在逻辑回归、支持向量机、K-均值聚类等算法中,都涉及到了凸函数的应用。通过利用凸函数的性质,我们可以更加有效地求解这些问题,从而得到更好的模型性能。
总的来说,凸函数是一类具有特殊性质的数学函数,其由来可以追溯到早期的数学家们的研究。在机器学习中,凸函数的应用非常广泛,它可以帮助我们更好地求解优化问题,从而得到更好的模型性能。
总结(精华)
- 凸函数之所以呈现凹状,与我们主观常识不太一样,是因为凸凹性的定义是基于函数在任意两点之间的线段与函数图像之间的位置关系。具体来说,如果一个函数在任意两点之间的线段都在函数图像之上,则该函数被称为凸函数;如果线段都在函数图像之下,则该函数被称为凹函数。
- 这个定义与我们日常生活中的直观感受可能不太一致,因为我们通常是根据一个物体或形状的表面来判断它是凸还是凹的。例如,一个凸起的山丘或球面通常被认为是凸的,而一个凹陷的坑洞或碗则被认为是凹的。然而,在数学中,凸凹性的定义是基于函数图像与线段之间的位置关系,而不是基于物体的表面形状。
- 因此,当我们看到一个凸函数的图像时,它可能呈现出凹状的外观,因为函数图像在任意两点之间的线段之上。这并不意味着函数本身是凹的,只是它的图像在视觉上呈现出凹状。同样地,凹函数的图像可能在视觉上呈现出凸状。
- 需要注意的是,凸凹性的定义在不同的领域和上下文中可能有所不同。在某些领域中,凸凹性的定义可能与数学中的定义相反。因此,在具体应用中,需要根据具体的定义和上下文来理解凸凹性。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献14条内容
已为社区贡献14条内容





所有评论(0)