1 iLQR背景

对于非线性模型，求解最优控制问题：

对于一个非线性的函数，为了计算极值，我们用原来的函数，线性近似或者二次函数近似，从而计算近似函数的下降点，通过迭代，最终得到原来函数的极值。

iLQR思想也借鉴了数值优化的迭代思想，对一个非线性极值问题，使用二阶泰勒展开去近似原始函数，求解每一次近似函数的极值，通过这种方式迭代地计算非线性曲线的极值

对于iLQR问题，因为$\dot{x}=f(x,u)$是非线性的，如果直接在原始的 LQR 计算框架中，无法得到解析解，此时V(x)是一个复杂的高维度非线性函数。观察LQR框架，Q(x,u)和V(x)都是二次函数。

将f(x,u)线性化，把复杂的cost-to-go函数V(x)泰勒展开为二阶，近似原来的V(x)，这样就可以用LQR框架计算轨迹

求解最优轨迹：先给定一条轨迹，然后设定需要的代价函数cost(x,u)，每一次迭代中都计算最优解，然后 cost 函数用来调整解，直到收敛

DDP ----->iLQR
DDP状态转移方程：二阶
iLQR状态转移方程：一阶

2 线性化

LQR：状态方程是线性的，代价函数是二次的，可以通过Riccai方程得到解析解。

然而对于非线性方程，得不到解析解，只能通过数值解来计算。所以在处理非线性方程问题时，可以将状态方程线性化，转化为常规LQR可以求解的方式

一般求解求解连续的 lqr 问题，使用 HJB 方程来计算。在 iLQR 中，一般将连续的状态方程转换成离散方程，从而使用动态规划原理来计算轨迹。

离散状态方程：
$$x_{t+1}=f(x_t,u_t)$$

代价函数：
$$\underset{{\mathbf{u}}_1,\dots ,{\mathbf{u}}_T}{\min }\sum _{t=1}^{T}c\left({\mathbf{x}}_t,{\mathbf{u}}_t\right)\text{ s.t. }{\mathbf{x}}_{t+1}=f\left({\mathbf{x}}_t,{\mathbf{u}}_t\right)$$
展开求和公式：
$$\underset{{\mathbf{u}}_1,\dots ,{\mathbf{u}}_T}{\min }c\left({\mathbf{x}}_1,{\mathbf{u}}_1\right)+c\left(f\left({\mathbf{x}}_1,{\mathbf{u}}_1\right),{\mathbf{u}}_2\right)+\cdots +c\left(f(f(\dots )\dots ),{\mathbf{u}}_T\right)$$
这个方程只包括控制量u，对控制量$u=u_0,u_1,...,u_N$求偏导，为了求出最优解。但是代价函数嵌套太多，求导不易。

贝尔曼最优性原理：未来状态只和当前状态有关，而和过去状态无关。

贝尔曼最优性原理：
Q k = g ( x k , u k ) + V k + 1 ( x k + 1 ) V k = min ⁡ { Q k } \begin{array}{c} Q_{k}=g\left(x_{k}, u_{k}\right)+V_{k+1}\left(x_{k+1}\right) \\ V_{k}=\min \left\{Q_{k}\right\} \end{array} Qk​=g(xk​,uk​)+Vk+1​(xk+1​)Vk​=min{Qk​}​

要想使得 k 阶段的 cost-to-go $V_k$最优，只需要$Q_k$取极小值，因为$V_{k+1}(x_{k+1})$在上一个阶段已经计算出来了，此时$Q_k$和$x_k,u_k$有关，状态量是受控制量影响的，所以计算得到最优的$u_k$即可

动态规划DP将计算$u=u_0,u_1,...,u_N$的过程，转变成了计算单步$u_k$的过程，然后$k=N$->0迭代，整体地控制量也就可以得到，这样求解就简单多了。然后利用上 DP 的整个 backward pass 和 forward pass，就可以得到整个解。

对于 ilqr 而言，将非线性的状态转移方程、目标函数泰勒展开，然后使用 lqr 求解方式去计算近似解，得到最后结果。

泰勒展开：
$$\begin{array}{l}f\left({\mathbf{x}}_t,{\mathbf{u}}_t\right)\approx f\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)+{\nabla }_{{\mathbf{x}}_t,{\mathbf{u}}_t}f\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)\left[\begin{array}{l}{\mathbf{x}}_t-{\hat{\mathbf{x}}}_t\\ {\mathbf{u}}_t-{\hat{\mathbf{u}}}_t\end{array}\right]\\ c\left({\mathbf{x}}_t,{\mathbf{u}}_t\right)\approx c\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)+{\nabla }_{{\mathbf{x}}_t,{\mathbf{u}}_t}c\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)\left[\begin{array}{l}{\mathbf{x}}_t-{\hat{\mathbf{x}}}_t\\ {\mathbf{u}}_t-{\hat{\mathbf{u}}}_t\end{array}\right]+\frac{1}{2}{\left[\begin{array}{l}{\mathbf{x}}_t-{\hat{\mathbf{x}}}_t\\ {\mathbf{u}}_t-{\hat{\mathbf{u}}}_t\end{array}\right]}^T{\nabla }_{{\mathbf{x}}_t,{\mathbf{u}}_t}^{2}c\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)\left[\begin{array}{l}{\mathbf{x}}_t-{\hat{\mathbf{x}}}_t\\ {\mathbf{u}}_t-{\hat{\mathbf{u}}}_t\end{array}\right]\end{array}$$
移项：
$$\begin{array}{rl}f\left({\mathbf{x}}_t,{\mathbf{u}}_t\right)-f\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)& \approx {\nabla }_{{\mathbf{x}}_t,{\mathbf{u}}_t}f\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)\left[\begin{array}{l}{\mathbf{x}}_t-{\hat{\mathbf{x}}}_t\\ {\mathbf{u}}_t-{\hat{\mathbf{u}}}_t\end{array}\right]\\ c\left({\mathbf{x}}_t,{\mathbf{u}}_t\right)-c\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)& \approx {\nabla }_{{\mathbf{x}}_t,{\mathbf{u}}_t}c\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)\left[\begin{array}{l}{\mathbf{x}}_t-{\hat{\mathbf{x}}}_t\\ {\mathbf{u}}_t-{\hat{\mathbf{u}}}_t\end{array}\right]+\frac{1}{2}{\left[\begin{array}{l}{\mathbf{x}}_t-{\hat{\mathbf{x}}}_t\\ {\mathbf{u}}_t-{\hat{\mathbf{u}}}_t\end{array}\right]}^T{\nabla }_{{\mathbf{x}}_t,{\mathbf{u}}_t}^{2}c\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)\left[\begin{array}{l}{\mathbf{x}}_t-{\hat{\mathbf{x}}}_t\\ {\mathbf{u}}_t-{\hat{\mathbf{u}}}_t\end{array}\right]\end{array}$$

$\delta x,\delta u$
$$\bar{f}\left(\delta {\mathbf{x}}_t,\delta {\mathbf{u}}_t\right)=\underset{{\nabla }_{{\mathbf{x}}_t,{\mathbf{u}}_t}f\left({\hat{\mathbf{x}}}_t,{\hat{\mathbf{u}}}_t\right)}{\underbrace{{\mathbf{F}}_t}}\left[\begin{array}{l}\delta {\mathbf{x}}_t\\ \delta {\mathbf{u}}_t\end{array}\right]$$

这样整个状态转移方程、目标函数变成和 lqr 一样的形式

状态转移方程：
$$f\left(x_k+\delta x,u_k+\delta u\right)=f(x)+\frac{\partial f}{\partial x}\delta x+\frac{\partial f}{\partial u}\delta u+\text{ 高阶项 }$$

对于非线性方程，通过泰勒展开，可以对原始的函数有不同程度的局部近似

3 离散化

前向欧拉离散化：
$$\dot{\tilde{\chi }}=\frac{\tilde{\chi }(k+1)-\tilde{\chi }(k)}{T}=A\tilde{\chi }+B\tilde{\mathbf{u}}$$
离散时间状态空间表达式：

G(T) ≈ TA+1
H(T) ≈ TB

4 Backward pass反向传播

动态规划两个常见的概念：动作价值函数$Q(x,u)$和价值函数$V(x)$

阶段k到阶段N，最优的cost叫做价值函数cost-to-go($V_{k->N}$，简写为$V_k$)
在阶段 k 这里，$u_k$可以有多种选择，每一种选择都会带来不同的 cost，所以，在这里又新增加一个概念叫做 action-value 函数 Q，影响 Q 取值的变量包括 x 和 u，所以一般写成$Q(x_k,u_k)$

动作价值函数有2个代价组成，一个代价是，在阶段 k，系统处于状态 x，当前动作 u 带来的代价 g(x,u)。另一个代价是上一个阶段 k+1 的最优代价 cost to go。所以，Q 表达式为$Q\left(x_i,u_i\right)=g\left(x_i,u_i\right)+V\left(x_{i+1}\right)=g\left(x_i,u_i\right)+V\left(f\left(x_i,u_i\right)\right)$

在 k 阶段，如果得到最优的$u_k$，那么得到最优的$V_k$， V ( x i ) = min ⁡ { Q ( x i , u i ) } V\left(x_{i}\right)=\min \left\{Q\left(x_{i}, u_{i}\right)\right\} V(xi​)=min{Q(xi​,ui​)}

Q泰勒展开：


$$\begin{gathered} \frac{1}{2}{\left[\begin{array}{l}\delta x_i\\ \delta u_i\end{array}\right]}^T\left[\begin{array}{cc}{Q}_{x_i^2}& Q_{x_i{u}_i}\\ Q_{u_i{x}_i}& Q_{u_i^2}\end{array}\right]\left[\begin{array}{l}\delta x_i\\ \delta u_i\end{array}\right]+{\left[\begin{array}{l}{Q}_{x_i}\\ Q_{u_i}\end{array}\right]}^T\left[\begin{array}{l}\delta x_i\\ \delta u_i\end{array}\right] \\ =\frac{1}{2}{\left[\begin{array}{c}1\\ \delta x\\ \delta u\end{array}\right]}^T\left[\begin{array}{ccc}0& Q_x^T& Q_u^T\\ Q_x& Q_{xx}& Q_{xu}\\ Q_u& Q_{ux}& Q_{uu}\end{array}\right]\left[\begin{array}{c}1\\ \delta x\\ \delta u\end{array}\right] \end{gathered}$$
价值函数 V 泰勒展开


𝛿𝑄也可以将泰勒展开式移项，表达为

𝛿𝑄的表达式中，其中


为了求解上式，将 g 展开（代价函数有时的符号也可以为𝑙）
$$\begin{array}{rl}\ell \left(x_i+\delta x_i,u_i+\delta u_i\right)& =\ell \left(x_i,u_i\right)+\delta \ell \left(x_i,u_i\right)\\ & \approx \ell \left(x_i,u_i\right)+\frac{\partial \ell \left(x_i,u_i\right)}{\partial x_i}\delta x_i+\frac{\partial \ell \left(x_i,u_i\right)}{\partial u_i}\delta u_i\\ & +\frac{1}{2}\delta x_i^T\frac{{\partial }^2\ell \left(x_i,u_i\right)}{\partial x_i^2}\delta x_i+\frac{1}{2}\delta u_i^T\frac{{\partial }^2\ell \left(x_i,u_i\right)}{\partial u_i^2}\delta u_i\\ & +\frac{1}{2}\delta x_i^T\frac{{\partial }^2\ell \left(x_i,u_i\right)}{\partial x_i\partial u_i}\delta u_i+\frac{1}{2}\delta u_i^T\frac{{\partial }^2\ell \left(x_i,u_i\right)}{\partial u_i\partial x_i}\delta x_i\\ & \triangleq \ell \left(x_i,u_i\right)+{\ell }_{x_i}^T\delta x_i+{\ell }_{u_i}^T\delta u_i+\frac{1}{2}\delta x_i^T{\ell }_{x_i^2}\delta x_i+\frac{1}{2}\delta u_i^T{\ell }_{u_i^2}\delta u_i\\ & +\frac{1}{2}\delta x_i^T{\ell }_{x_i{u}_i}\delta u_i+\frac{1}{2}\delta u_i^T{\ell }_{u_i{x}_i}\delta x_i\end{array}$$
继续定义符号：

所以，根据向量的链式求导法则

已知$Q_x^T$，根据矩阵运算性质，计算他的转置矩阵，

根据 bellman 最优性原理，可以对系统的状态进行反向传播，即从终端状态{$x_N,u_N$}计算到{$x_0,u_0$}
（1）首先计算终端的 Q，V
$$V_N\left(x_N+\delta x_N\right)=V_N\left(x_N\right)+\frac{\partial V_N}{\partial x}\delta x_N+\frac{1}{2}(\partial x{)}^T\frac{{\partial }^2{V}_N}{\partial x^2}\delta x$$
对于末端$x_N$而言，一般不再施加控制,所以控制量$u_N=0$，此时的最优值函数往往是一个平方项
$V_N\left(x_N\right)=g_N\left(x_N\right)=\frac{1}{2}{\left(x_N-x_{rN}\right)}^T{R}_N\left(x_N-x_{rN}\right)$
那么

这样的话，得到终点的$V_x^T,V_{xx}$，就可以得到前一个点的$Q_u,Q_{xx},Q_{xu}$

（2）继续分析剩余状态，已知动作值函数 Q，为了计算最优控制序列，对𝛿𝑢直接求导

为了使得𝛿𝑄最小，令导数为 0

得到最优𝛿u

其中，
得到最优𝛿𝑢 之后，将其代入到𝛿𝑄中，利用 bellman 最优性原理，Q 和 V 的关系是

𝛿𝑄和𝛿𝑉的关系是什么呢？在$Q_k$是最优动作值函数时，那么$V_k(x_k)=Q_k(x_k)$，那么即使再增加一个小扰动𝛿𝑥,$V_k\left(x_k+\delta x\right)=Q_k\left(x_k+\delta x\right)$
联立



综述：
对于反向传播：如果知道𝑘+1阶段的$V_x(k+1)$，$V_{xx}(k+1)$，那么就能得到 k 阶段的$Q_x,Q_u,Q_{xx},Q_{xu}$，那么继续可以得到 k 阶段的反馈增益𝐾 𝑑，那么继续得到$\delta u_k$，然而由于$\delta x_k$具体值未知，不能确定具体的$\delta x_k$，没关系，这里不知道具体值并不影响整体计算。然后此时再刷新 k 阶段的$V_x(k)$，$V_{xx}(k)$，进入下一个循环

在反向传播中，并没有更新具体的 x 值和 u 值，但是更新了反馈增益 K,后续在正向传播的时候就可以利用上

5 Forward pass正向传播

和常规的 LQR 不同，iLQR 的 forward pass 的时候需要使用非线性的状态转移方程来更新。在反向传播的时候，已经更新了反馈增益序列{$K_1,K_2,...,K_N$}，根据方程$\delta u_k{}^{\ast }=-Q_{uu}^{-1}\left(Q_{ux}\delta x_k+Q_{u_k}\right)=K\delta x_k+d$，如果已知$\delta x$，那么就可以得到$\delta u_k^{\ast }$

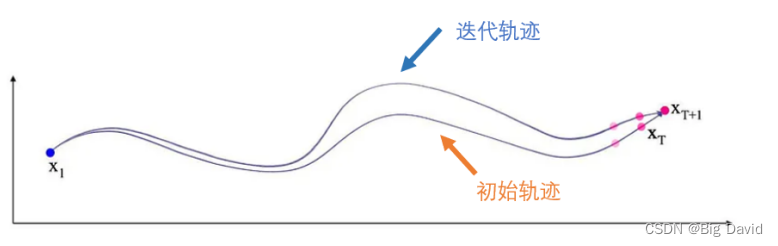
使用两次迭代轨迹点 k 的差分，更新$\delta x_k$，注意，这里并不是使用轨迹上前后两个点的位置差分，而是使用两条轨迹点，例如，在迭代i-1次，得到一条轨迹，在迭代i次，也会产生一条轨迹，那么在轨迹点k处，有$\delta x_k=x_k^i-x_k^{i-1}$，这样可以更新$\delta u_k^{\ast }$，因为$\delta u_k=d_k+K_k\delta x_k$，然后更新控制量$u_k$，因为$u_k^i=u_k^{i-1}+\delta u_k$，再根据状态转移方程，使用当前点的状态值和控制值，来更新下一个 k+1 轨迹点的值$x_{k+1}^i=f\left(x_k^i,u_k^i\right)$，这样一直增大 k 的值，整条轨迹就得到更新

6 iLQR 的迭代

在一次循环中，轨迹得到更新，那么 cost 和值函数 V 也得到更新，为了让 cost 最小，继续微调𝛿𝑢的值，直到算法收敛。假设已经给出一个较好的初始轨迹，我们对初始轨迹进行调整优化即可。收敛的准则是，

即可以使用最优值函数 V 来计算，起点到终点的cost_to_go是$J=V_{0->N}$，每一次迭代，都有$J=V_{0->N}$，然后使用前后两次迭代的性能指标，判断是否收敛

iLQR 可以存在 3 个循环

• 一个外循环，负责调整𝛿𝑢的值，从而改善轨迹性能
• 一个内循环，用来反向传播计算反馈增益
• 还有一个内环，正向传播计算具体的𝛿𝑢，𝛿𝑥,以及u,x

7 iLQR

iLQR vs DDP
f(x,u)泰勒展开，一个取一阶，一个取二阶，与DDP相比，iLQR不再具有2阶收敛性，然而使用二阶计算，会增加计算负担，影响后面的计算性能

对于iLQR问题，优化问题形式：
经典iLQR：
$$\begin{array}{rl}{x}^{\ast },u^{\ast }& =\underset{x,u}{\mathrm{argmin}}\left\{\varphi \left(x_N\right)+\sum _{k=0}^{N-1}{L}^k\left(x_k,u_k\right)\right\}\\ \text{ s.t. }{x}_{k+1}& =f^k\left(x_k,u_k\right),k=0,1,\dots ,N-1\\ x_0& =x_{\text{start }}\end{array}$$优化变量包括x（状态量）和u（控制量），目标就是找到最优的x和u，使得cost function达到最小。

cost function第一项描述终点状态，一般终点没有控制量，最后一个点的控制量不定义或者默认为0。后一项可以说是转移的cost，也就是给一个输入量，从一个状态转移到另一个状态过程中的cost是多少，一共有N-1步
系统约束：第一项就是运动学/状态转移的约束，第二项是给定一个初始状态，需要给一个初始状态，才能设计出最好的u来驱动系统获得一条轨迹。

带约束的iLQR
$$\begin{array}{rl}{x}^{\ast },u^{\ast }& =\underset{x,u}{\mathrm{argmin}}\varphi \left(x_N\right)+\sum _{k=0}{L}^k\left(x_k,u_k\right)\\ \text{ s.t. }{x}_{k+1}& =f\left(x_k,u_k\right),k=0,1,\dots ,N-1\\ x_0& =x_{\text{start }}\\ d\left(x_k,O_j^k\right)& >0,k=1,2,\dots ,N\cdot j=1,2,\dots ,m\\ \underline{u}& <u_k<\bar{u},k=1,2,\dots ,N-1\end{array}$$施加一些显式的约束，第一项是轨迹点的距离与障碍物的距离要大于0，第二项是动力学可行性约束。