【算法】最短路径——弗洛伊德 (Floyd) 算法
本文介绍了弗洛伊德 (Floyd) 算法的相关知识。
1.概述
(1)弗洛伊德 (Floyd) 算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与 Dijkstra 算法类似。该算法名称以创始人之一、1978 年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
(2)弗洛伊德 (Floyd) 算法的具体思路如下:
- 创建一个二维数组 dist,用于存储任意两个顶点之间的最短路径长度。
- 初始化 dist 数组,将每条边的权重赋值给对应的 dist[i][j],其中 i 和 j 分别表示边的起点和终点。
- 使用三重循环,分别遍历每一个顶点 k,将顶点 k 作为中间节点,更新 dist 数组。
- 对于每一对顶点 i 和 j,如果
dist[i][j]大于dist[i][k] + dist[k][j],则更新 dist[i][j] 为 dist[i][k] + dist[k][j]。 - 最终,dist 数组中存储的就是每对顶点之间的最短路径长度。
该算法的核心思想是通过动态规划逐步构建最短路径。通过逐渐扩展考虑的中间节点集合,可以确保得到最终的最短路径。通过多次迭代,每对顶点之间的最短路径逐渐更新,直到遍历完所有的中间节点,得到最后的最短路径矩阵。
(3)弗洛伊德 (Floyd) 算法的时间复杂度和空间复杂度分别如下:
- 时间复杂度为 O(V3),弗洛伊德算法使用三重循环来迭代更新所有顶点对之间的最短路径,其中 V 表示图中顶点的数量。因此,算法的时间复杂度为 O(V3)。
- 空间复杂度为 O(V2):算法需要使用一个二维数组来存储图中顶点对之间的最短路径距离,因此空间复杂度为 O(V2)。
有关 Dijkstra 算法的具体介绍可以参考【算法】最短路径——迪杰斯特拉 (Dijkstra) 算法这篇文章。
2.代码实现
(1)有关 Floyd 算法分别使用邻接矩阵和邻接表实现的说明如下:
- Floyd 算法可以使用邻接表实现,但相比邻接矩阵,使用邻接表会增加一些复杂度,因为邻接表中存储了每个节点的出边信息,并没有存储到达该节点的边的信息。因此,在计算两个节点之间的距离时,需要遍历邻接表中连接这两个节点的所有边,这可能会使得算法的时间复杂度和空间复杂度都增加。另外,使用邻接表需要额外的开销来维护节点之间的关系。
- 具体实现时,可以将每个节点的出边信息存储在一个链表、向量等动态数据结构中。为了能够以常数时间检查两个节点之间是否有边,可以使用哈希表来存储每个节点的出边信息。在遍历所有节点对时,对于每对节点 i 和 j,需要分别遍历它们的出边列表,以找到连接它们的路径。
- 总之,虽然 Floyd 算法可以使用邻接表实现,但邻接矩阵更为简单和直观,并且在实现中运行时间更短和更节省空间。只有在图的规模比较大、稀疏程度比较高时,才考虑使用邻接表来表示图和实现弗洛伊德算法。
(2)下面给出 Floyd 算法的邻接矩阵实现:
class Solution {
/*
graph: 用于表示图的邻接矩阵
返回值: 最短路径矩阵
*/
public int[][] floyd(int[][] graph) {
int n = graph.length;
//初始化距离矩阵为邻接矩阵
int[][] dist = new int[n][n];
for (int i = 0; i < n; i++) {
System.arraycopy(graph[i], 0, dist[i], 0, n);
}
//三重循环,依次计算每对节点之间的最短路径
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][k] != Integer.MAX_VALUE && dist[k][j] != Integer.MAX_VALUE) {
//如果经过中间节点 k 更短,则更新路径长度
dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
return dist;
}
}
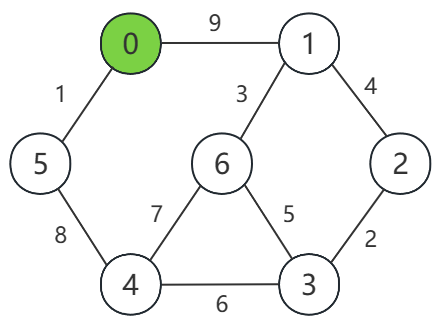
(3)本测试中的加权无向图如下所示。

class Test {
public static void main(String[] args) {
//图的顶点数
int n = 7;
int[][] graph = new int[n][n];
//初始化邻接矩阵,初始化为 Integer.MAX_VALUE 表示不可达
for (int i = 0; i < n; i++) {
Arrays.fill(graph[i], Integer.MAX_VALUE);
graph[i][i] = 0;
}
//添加图的边
graph[0][1] = 9;
graph[0][5] = 1;
graph[1][0] = 9;
graph[1][2] = 4;
graph[1][6] = 3;
graph[2][1] = 4;
graph[2][3] = 2;
graph[3][2] = 2;
graph[3][4] = 6;
graph[3][6] = 5;
graph[4][3] = 6;
graph[4][5] = 8;
graph[4][6] = 7;
graph[5][0] = 1;
graph[5][4] = 8;
graph[6][1] = 3;
graph[6][3] = 5;
graph[6][4] = 7;
Solution solution = new Solution();
int[][] dist = solution.floyd(graph);
//输出最短路径矩阵
System.out.println("The shortest path matrix:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][j] == Integer.MAX_VALUE) {
System.out.print("INF \t");
} else {
System.out.print(dist[i][j] + " \t");
}
}
System.out.println();
}
}
}
输出结果如下:
The shortest path matrix:
0 9 13 15 9 1 12
9 0 4 6 10 10 3
13 4 0 2 8 14 7
15 6 2 0 6 14 5
9 10 8 6 0 8 7
1 10 14 14 8 0 13
12 3 7 5 7 13 0
3.扩展
(1)如果要求出每对顶点最短路径之间依次经过的节点,我们可以再增加一个矩阵来保存路径信息。设 paths[i][j] 表示节点i到节点j的最短路径经过的顶点序列。则 paths[i][j] 的计算如下:
- 如果 dist[i][j] 为 INF(即节点 i 无法到达节点 j),则 paths[i][j] 为
null。 - 如果 i 和 j 之间有一条边(即 graph[i][j] 不为 INF),则 paths[i][j] 的值为
[i, j]。 - 否则,如果 dist[i][j] 可由 i 到达一个中间节点 k,然后由 k 到达 j 的路径更短,则在 paths[i][j] 中增加 k,并将 i->j 的最短路径更新为
i->k->j。
(2)具体实现时,可以在弗洛伊德算法中增加一个与 dist 矩阵同样大小的 paths 矩阵,通过修改弗洛伊德算法中更新距离的语句,同时更新 paths 矩阵中的值,最终输出 paths 矩阵中的每个元素即可。具体实现如下所示:
class Solution {
/*
graph: 用于表示图的邻接矩阵
返回值: 路径矩阵
*/
public int[][] floydWithPath(int[][] graph) {
int n = graph.length;
//初始化距离矩阵和路径矩阵
int[][] dist = new int[n][n];
int[][] paths = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dist[i][j] = graph[i][j];
if (graph[i][j] != Integer.MAX_VALUE) {
paths[i][j] = j;
} else {
paths[i][j] = -1;
}
}
}
//三重循环,依次计算每对节点之间的最短路径
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (dist[i][k] != Integer.MAX_VALUE && dist[k][j] != Integer.MAX_VALUE) {
// 如果经过中间节点 k 更短,则更新路径长度和路径矩阵
if (dist[i][j] > dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
paths[i][j] = paths[i][k];
}
}
}
}
}
return paths;
}
}
(3)本测试中的加权无向图与上面一样,测试代码如下所示:
class Test {
public static void main(String[] args) {
//图的顶点数
int n = 7;
int[][] graph = new int[n][n];
//初始化邻接矩阵,初始化为 Integer.MAX_VALUE 表示不可达
for (int i = 0; i < n; i++) {
Arrays.fill(graph[i], Integer.MAX_VALUE);
graph[i][i] = 0;
}
//添加图的边
graph[0][1] = 9;
graph[0][5] = 1;
graph[1][0] = 9;
graph[1][2] = 4;
graph[1][6] = 3;
graph[2][1] = 4;
graph[2][3] = 2;
graph[3][2] = 2;
graph[3][4] = 6;
graph[3][6] = 5;
graph[4][3] = 6;
graph[4][5] = 8;
graph[4][6] = 7;
graph[5][0] = 1;
graph[5][4] = 8;
graph[6][1] = 3;
graph[6][3] = 5;
graph[6][4] = 7;
Solution solution = new Solution();
int[][] paths = solution.floydWithPath(graph);
System.out.println("The path matrix:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (paths[i][j] == -1) {
System.out.print("null ");
} else {
List<Integer> p = new ArrayList<>();
int cur = i;
while (cur != j) {
p.add(cur);
cur = paths[cur][j];
}
p.add(j);
System.out.print(p + " ");
}
}
System.out.println();
}
}
}
输出结果如下:
The path matrix:
[0] [0, 1] [0, 1, 2] [0, 1, 2, 3] [0, 5, 4] [0, 5] [0, 1, 6]
[1, 0] [1] [1, 2] [1, 2, 3] [1, 6, 4] [1, 0, 5] [1, 6]
[2, 1, 0] [2, 1] [2] [2, 3] [2, 3, 4] [2, 1, 0, 5] [2, 1, 6]
[3, 2, 1, 0] [3, 2, 1] [3, 2] [3] [3, 4] [3, 4, 5] [3, 6]
[4, 5, 0] [4, 6, 1] [4, 3, 2] [4, 3] [4] [4, 5] [4, 6]
[5, 0] [5, 0, 1] [5, 0, 1, 2] [5, 4, 3] [5, 4] [5] [5, 0, 1, 6]
[6, 1, 0] [6, 1] [6, 1, 2] [6, 3] [6, 4] [6, 1, 0, 5] [6]
3.应用
(1)弗洛伊德 (Floyd) 算法的应用场景包括但不限于以下几个方面:
- 多源最短路径问题:弗洛伊德算法可以解决图中任意两个顶点之间的最短路径问题。这在路由算法、网络通信中非常有用,可以帮助确定从一个网络节点到其他节点的最短路径。
- 公交网络规划:在城市公交系统中,弗洛伊德算法可以用于计算任意两个站点之间的最短路径,从而帮助规划公交线路和乘车路线。
- 遗传算法中的距离计算:在遗传算法中,常常需要计算个体之间的距离或相似度,弗洛伊德算法可以用于计算从一个个体到其他个体之间的最短距离,以便进行后续的选择、交叉和变异操作。
- 最优路径规划:弗洛伊德算法可以用于在地图导航系统中计算最短路径,帮助用户在城市道路网中找到最佳的行驶路径。
- 交通流量优化:弗洛伊德算法可以用于计算交通网络中的最短路径,以优化交通流量分配,避免拥堵和优化道路资源利用。
(2)大家可以去 LeetCode 上找相关的 Floyd 算法的题目来练习,或者也可以直接查看 LeetCode 算法刷题目录 (Java) 这篇文章中的最短路径章节。如果大家发现文章中的错误之处,可在评论区中指出。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容






所有评论(0)