分享本周所学——概率论：贝叶斯更新详解

大家好，欢迎来到《分享本周所学》第六期。本人是一名人工智能初学者，因为马上要上大学了嘛，就想着提前稍微预习一下大一课程。我预习的这门课叫Mathematical Techniques for Computer Science，是一门针对计算机的数学课，所以这里面有很多内容会面向数学在计算机当中的实际应用。最近一周我学了一下基础的概率论，然后发现这里面有贝叶斯更新这个内容。我一一想，这不是机器学习的

RFdragon

8946人浏览 · 2022-09-09 18:13:38

RFdragon · 2022-09-09 18:13:38 发布

这篇文章主要参考了曼彻斯特大学一年级课程Mathematical Techniques for Computer Science的教材。教材是公开的，链接如下：

2023年5月10日更新：其实应该早点在这更新一下的。目前炉石传说和绝大部分其他暴雪游戏的国服都已经停服几个月了，之后看到这篇文章的人里面可能玩过炉石传说的会越来越少，大家可以带入一下自己喜欢的其他卡牌游戏的职业和牌名。委屈大家了。

9月20日更新：很抱歉，教材现在似乎只对在读学生公开了，根据学校的教学内容版权要求，我不得不移除文章内的所有教材链接，请大家谅解。

上期文章链接：https://blog.csdn.net/weixin_48978134/article/details/125770821https://blog.csdn.net/weixin_48978134/article/details/125770821

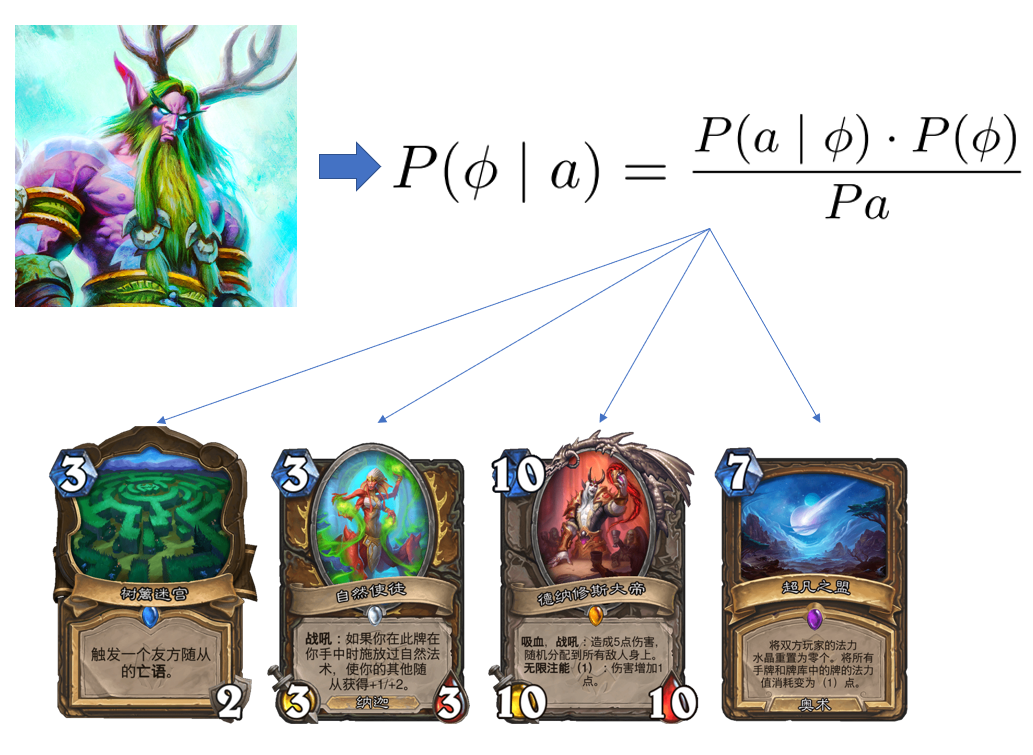
本期封面：

一、学贝叶斯更新需要知道点啥啊

贝叶斯更新是需要一点点前置知识的，但仅仅是一点点。你只需要知道什么是条件概率和全概率公式就可以了。如果你已经知道了的话，可以直接看第二章。

1. 条件概率

顾名思义，条件概率就是满足一些条件的情况下，某个事件发生的概率。什么意思呢？举个非常常见的例子。有一天，我闲的没事，决定让你猜我的电脑多少钱，然后给了你两个选项：5000块左右和10000块左右。

我们假设世界上所有的电脑都只有5000块左右和10000块左右这两个价位，有70%的人用5000块左右的电脑，剩下30%的人用10000块左右的电脑。我们可以根据这个数据来画一个非常简陋的表格：

我们用P(A)来表示一个事件A发生的概率。根据这个表格，你可以轻易的推断出P(我的电脑5000块左右)>P(我的电脑10000块左右)，所以，你理所当然会猜我的电脑5000块左右。

但是，这时我们给表格引入一个新的维度：

此时，你得知我开的车在一百万以上，那么也许你就要改变自己的猜测了，因为你要比较的两个概率从P(我的电脑5000块左右)和P(我的电脑10000块左右)变成了P(我的电脑5000块左右|我开一百万以上的车)和P(我的电脑10000块左右|我开一百万以上的车)。P(A|B)表示A在B发生的条件下发生的概率，我们把这种概率称作条件概率。

那怎么计算条件概率呢？其实就是用一个非常简单公式：

$P(A|B) = \frac {P(A \cap B)} {P(B)}$

这里 $P(A \cap B)$ 表示A和B同时发生的概率，称作A和B的联合概率。

这个公式其实很好理解，A在B发生的条件下发生的概率，其实就是A和B同时发生的概率在B发生的概率里所占的比例。根据上面的表格，我们知道P(我的电脑5000块左右 $\cap$ 我开一百万以上的车)是0.002，而P(我的电脑10000块左右|我开一百万以上的车)是0.008。

根据这个公式，我们可以计算出了P(我的电脑5000块左右|我开一百万以上的车)是0.2，而P(我的电脑10000块左右|我开一百万以上的车)是0.8。因此，显然猜我的电脑在10000左右是更好的选择。

然而现实中我既没有10000左右的电脑也没有一百万的车。唉……

2. 全概率公式

什么是全概率公式呢？我们再看一个例子。

你现在想计算我出门带伞的概率。不管是晴天、阴天还是雨天，我都有可能出门带伞。但是显然啊，在不同的天气下我出门带伞的概率是不同的。假设我晴天有1%的概率带伞、阴天有30%的概率带伞、雨天有90%的概率带伞。另外，你还知道，我住的城市有50%的概率是晴天，有30%的概率是阴天，有20%的概率是雨天。那么，综合以上这些信息，我在任意一天出门带伞的概率是多少呢？

这就要用到全概率公式了：

$P(A)=P(A|B_{1}) \times P(B_{1})+P(A|B_{2}) \times P(B_{2})+...+P(A|B_{n}) \times P(B_{n})$

如果写得简洁一点就是：

$P(A)= \sum_{i=1}^{n} P(A|B_{i}) \times P(B_{i})$

这里面，A是我们要计算概率的事件， $B_{1}$ , $B_{2}$ , $B_{3}$ ,…, $B_{n}$ 是两两互斥的事件，并且它们的概率之和为1。为了以防有人不知道，这里提一句，如果两个事件是互斥事件，说明它们不可能同时发生。

这个公式也很好理解。我们要计算一个事件发生的概率，可以把这个事件拆分成不同的情况，每种情况下A发生的概率就是公式中的 $P(A|B_{i})$ ，然后再乘上发生这种情况的可能性，也就是 $P(B_{i})$ 。

我们这里要计算的是P(我出门带伞)，那么我们可以把它拆分成P(我出门带伞|今天是晴天)×P(今天是晴天)+P(我出门带伞|今天是阴天)×P(今天是阴天)+P(我出门带伞|今天是雨天)×P(今天是雨天)。晴天、阴天、雨天显然是互斥事件，而且它们的概率之和为1，因此我们可以使用全概率公式。我们把上面的条件带入公式，就可以得到我任何一天出门带伞的概率是0.275。

二、啥是贝叶斯更新啊

要想搞清楚贝叶斯更新，我们要先搞清楚四个概念：先验概率、后验概率、证据和似然。这四个概念听起来很高级，但其实很好理解。为了方便理解，我们设想这样一个场景。你正在玩一个叫作《炉石传说》的卡牌游戏，这个卡牌游戏允许你选择一些卡牌来组成一个套牌，然后再用这个套牌去与其他玩家对战。对战过程中，双方并不能知道对方的套牌，但是可以根据对方使用的卡牌来进行猜测。作为一个新手，你总是被一些自己预料不到的牌扭转局势，因此，你认为在对战中猜测对手的套牌是很有必要的。在一场对战中，你决定要用贝叶斯更新来猜测对方的套牌。

1. 先验概率

在开始测之前，你觉得自己应该先预估一下对方有可能使用什么套牌。这个卡牌游戏有10个职业，每个职业能够使用的套牌都不同。在对战开始前，你可以看到对方的职业，所以你也可以根据对方的职业来预估对方的套牌。假设你看到对方是德鲁伊，德鲁伊常见的套牌有：亡语德鲁伊（亡语德）、快攻德鲁伊（快攻德）、德纳修斯大帝德鲁伊（大帝德）和超凡之盟德鲁伊（超凡德）（数据来源于2022年9月标准天梯）。但是，你并不能确定对方到底是这四个套牌中的哪一个。因此，你将这四个套牌的预估概率全部设为0.25。

这样以来，我们就得到了一个概率表。这个概率表就是先验概率，表示进行贝叶斯更新之前预估的概率。

2. 似然

第一回合，你的对手使用了一张卡牌，是暗礁德鲁伊！可恶，竟然在第一回合就使用了如此强大的卡牌，看来对手的实力不容小觑。你并没有被这张暗礁德鲁伊打得不知所措，而是冷静下来，开始分析对手的套牌。你将“对手第一回合使用了暗礁德鲁伊”这个事件记为事件 $a_{1}$ 。

快攻德、大帝德和超凡德都有可能携带暗礁德鲁伊，但这三个套牌第一回合打出暗礁德鲁伊的概率并不是均等的。而亡语德则不太可能携带暗礁德鲁伊。我们可以根据下面的表格来描述不同套牌第一回合打出暗礁德鲁伊的概率。

这个表格就是我们的似然。那具体什么是似然呢？可以说似然是一个和概率相反的概念。概率是根据已知的条件计算某个事件发生的可能性，而似然则是通过发生的事件去反推概率。比如，在我们的例子中，发生的事件是“对手第一回合使用暗礁德鲁伊”，而大帝德第一回合使用暗礁德鲁伊的概率是最大的，我们就可以反推出对方的套牌有较大概率是大帝德。

有的朋友可能要问了，这个似然是怎么算出来的呢？嗯，这个是我根据这四个德鲁伊套牌携带暗礁德鲁伊的情况和一般情况下的出牌思路估出来的，不一定准。如果你认为我给出的似然有问题，以你为准。

3. 证据因子

得到先验概率和似然之后，我们还差一步就可以进行贝叶斯更新了。我们现在需要计算证据因子。

什么是证据因子呢？我们在根据观察到的某个事件去估计其他事件发生的概率时，我们观察到的事件发生的概率就是证据因子。比如在这个例子中，我们根据事件 $a_{1}$ 估计“对方的套牌是亡语德/快攻德/大帝德/超凡德”的概率，那么P( $a_{1}$ )就是证据因子。

那怎么计算对方第一回合使用暗礁德鲁伊的概率呢？这里可以使用全概率公式，把P( $a_{1}$ )转化成P( $a_{1}$ |亡语德)×P(亡语德)+P( $a_{1}$ |快攻德)×P(快攻德)+P( $a_{1}$ |大帝德)×P(大帝德)+P( $a_{1}$ |超凡德)×P(超凡德)。我们可以计算出结果为0.13。

4. 后验概率

现在，我们已经有了先验概率、似然和证据因子，可以计算用贝叶斯更新来计算后验概率了。我们先来看一下贝叶斯更新的公式：

$P(\phi | a)=\frac{P(a| \phi) \times P(\phi)}{P(a)}$

这里面，Φ是我们要使用贝叶斯更新计算概率的事件，也就是“对方的套牌是亡语德/快攻德/大帝德/超凡德”，而a是我们观察到的事件，也就是“第一回合使用暗礁德鲁伊”。相信大家可以看出来，等式右侧的P(a|Φ)是似然，P(Φ)是先验概率，而P(a)是证据因子。等式左侧的P(Φ|a)就是后验概率，也是我们要计算的概率。

我们以亡语德为例。对方套牌是亡语德的后验概率P(亡语德| $a_{1}$ )=P( $a_{1}$ |亡语德)×P(亡语德)÷P( $a_{1}$ )=0.019。我们也可以用同样的方法算出P(快攻德| $a_{1}$ )=0.138、P(大帝德| $a_{1}$ )=0.549、P(超凡德| $a_{1}$ )=0.294。我们可以验算一下，0.019+0.138+0.549+0.294刚好等于1。

这样，根据对手第一回合使用了暗礁德鲁伊这一事件，我们就可以推出对手的套牌为亡语德、快攻德、大帝德和超凡德的概率分别为：

这就是一次完整的贝叶斯更新的流程：估计先验概率、计算似然和证据因子、利用贝叶斯更新公式计算后验概率。

虽然我们现在还没有足够的证据来证明对手使用的具体是什么套牌，但已经基本能够排除对方不是亡语德了。为了进一步确定对手使用的套牌，我们还需要继续观察对手出的牌，并使用贝叶斯更新计算新的概率。注意，我们前一次贝叶斯更新中算出的后验概率，会在下一次贝叶斯更新中作为先验概率。

5. 复习一遍贝叶斯更新流程

第二回合，你的对手使用了应急木工！不妙，又是一张如此强力的卡牌，仅仅花费两点法力水晶，就获得了两张额外的卡牌，还在战场上召唤了一个足足有两点攻击力的可怕怪物！

沉着冷静的你将对手第二回合使用应急木工记为事件 $a_{2}$ 。你脑中飞快地将似然计算了出来：

随后，将之前计算出的后验概率作为新的一次贝叶斯更新的先验概率，又计算出了证据因子：P( $a_{2}$ )=P( $a_{2}$ |亡语德)×P(亡语德)+P( $a_{2}$ |快攻德)×P(快攻德)+P( $a_{2}$ |大帝德)×P(大帝德)+P( $a_{2}$ |超凡德)×P(超凡德)=0.3。

最后，根据贝叶斯更新公式，你计算出了新的后验概率：