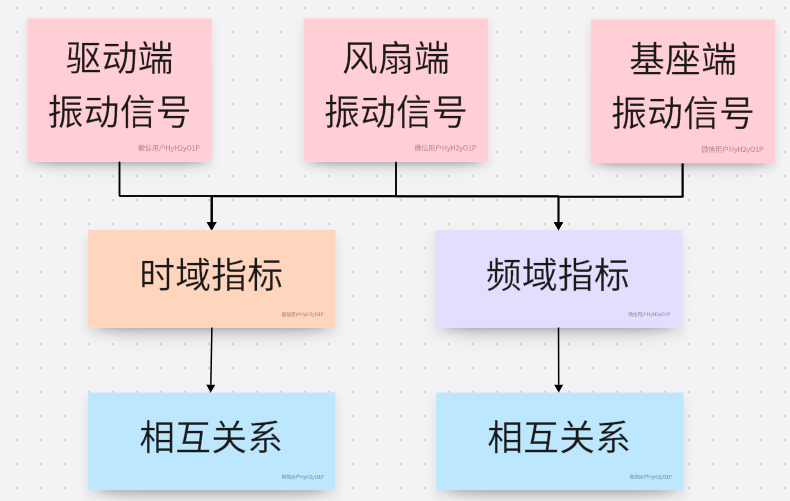
信号特征提取——常用时域和频域指标
信号处理中,一些常用的时域、频域指标
1、概括
在旋转机械的信号处理中,时域波形和频域波形的特征提取也是一个重要的话题。它能综合评价信号的某种特性,如冲击、波动、频率分布等,在故障诊断中也到了广泛的应用。
因此,本文归纳总结了一些常用的时域波形指标(11个)和频域波形指标(13个),以西储大学内圈故障数据(105.mat)为例,采用不同特征指标,分析不同测点位置处信号的之间的差异。具体技术路线如下:

关于时域指标和频域指标,参考了一些文献和一些博客介绍:
1.雷亚国.混合智能技术及其在故障诊断中的应用研究[D].西安交通大学,2007.
2.信号处理各项指标时域与频域指标https://zhuanlan.zhihu.com/p/621622520
3.频域特征指标及其MATLAB代码实现(重心频率、均方频率、均方根频率、频率方差、频率标准差)https://zhuanlan.zhihu.com/p/425141767
代码采用了Matlab 2024a进行运行,欢迎大家测试和提出问题!
2、时域指标
在时域指标中,主要分为有量纲的指标和无量纲的指标。有量纲的指标主要包括:均值、标准差、均方根值、峰值、峰峰值。无量纲的指标主要包括:峰值因子、偏度、峭度、脉冲因子、波形因子和裕度因子。在介绍这些指标前,假设每个采样周期内采集的振动信号为X=[x(1),...,x(i),...,x(N)],N表示单个采样周期内振动信号的采样点数。
1、均值表示振动信号的偏移量,计算如下:
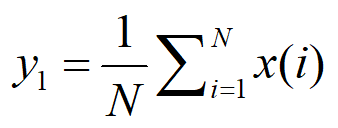
2、标准差表示振动信号的波动程度,计算如下:
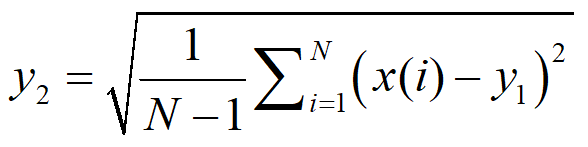
3、均方根值(RMS)表示振动信号在一段时间内的能量大小,计算如下:
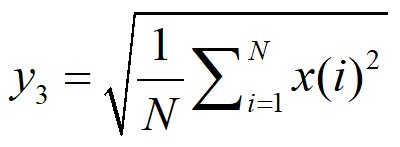
4、峰值(Peak)表示一段时间内振动信号的幅值的最大值,计算如下:
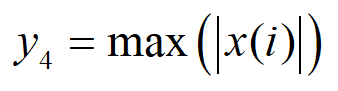
5、峰-峰值(Peak-to-Peak)表示一段时间内振动信号幅值最大值和最小值之间的差值,它反应了信号的变化范围,计算如下:
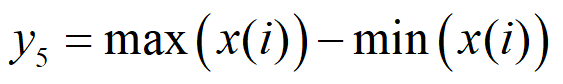
6、峰值因子(Crest Factor)表示振动信号中尖峰的大小,它为峰值和均方根值的比值,计算如下:
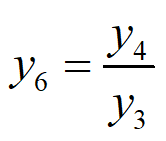
7、偏度(Skewness)能衡量振动信号概率密度函数的偏斜程度,它是振动信号的三阶标准化矩,计算如下:
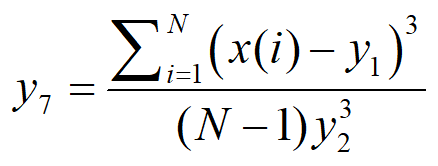
8、峭度(Kurtosis)表示一段时间内信号分布的尖锐程度,它是振动信号的四阶标准化矩,计算如下:
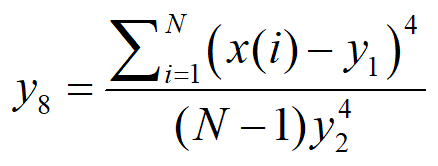
9、脉冲因子(Impulse Factor)能用来检测信号中是否含有冲击成分,计算如下:
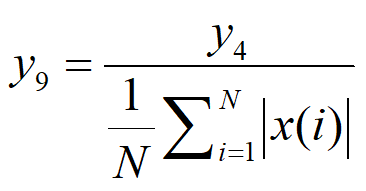
10、波形因子(Form Factor)也能反映信号波形的尖锐程度,它比脉冲因子更加稳定,计算如下:
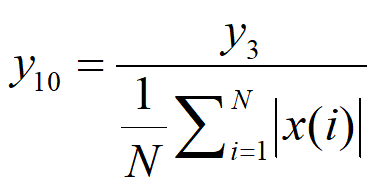
11、裕度因子(Clearance Factor)也能评估设备的故障程度,计算如下:
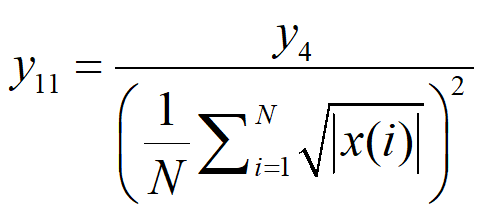
3、频域指标
在频域指标中,有一些具体含义的指标,如:频率的均值、频率重心、均方根频率、标准差频率。同时,一些不常用的指标也进行了整理,具体如下表所示。这里,假设s(k)是信号x(n)的频谱,k=1,2,...,K, K是谱线数,f(k)是第k条谱线的频率值(在下文中,f_k(k是下角标)就是f(k))。
1、频率的均值表示信号在频域内不同频率成分幅值的均值,计算如下:
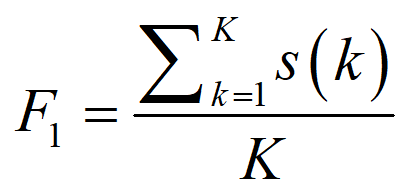
2、频率重心表示信号频谱的重心位置,描述了频谱中分量较大的峰值对用的横坐标频率,计算如下:
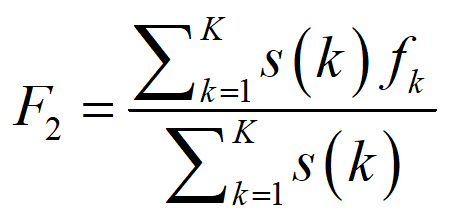
3、均方根频率能描述信号频域内整体能量分布情况,计算如下,而频率重心主要描述信号的主频带位置:
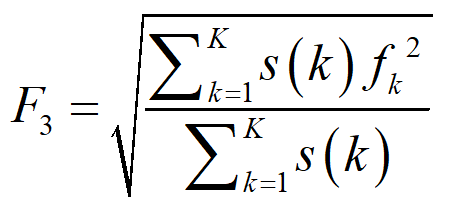
4、标准差频率反映了信号频谱的离散程度或集中程度(这里分子根号下选择了绝对值,部分论文中采用括号会出现根号下的负数,欢迎大家批评指正),计算如下:
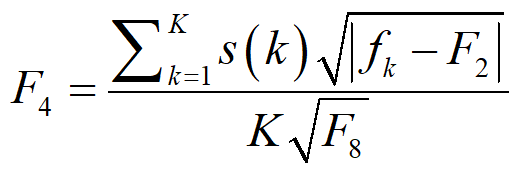
其余指标的计算等式具体如下:

4、具体案例

实验数据采用凯斯西楚大学(CWRU)的轴承数据,相关数据说明可参考如下软文:
本文选择了0HP、1797rpm的105.mat数据,它为内圈故障,缺陷尺寸为0.007英寸。该信号的采样频率为12000Hz,分别选择了驱动端、风扇端和基座端的数据,每个位置处信号的长度为4096,利用上述时域和频域指标,分析不同位置处信号之间的差异。
5、结果分析
分析驱动端、风扇端和基座端的振动信号,其时域波形和频域波形如下图所示:
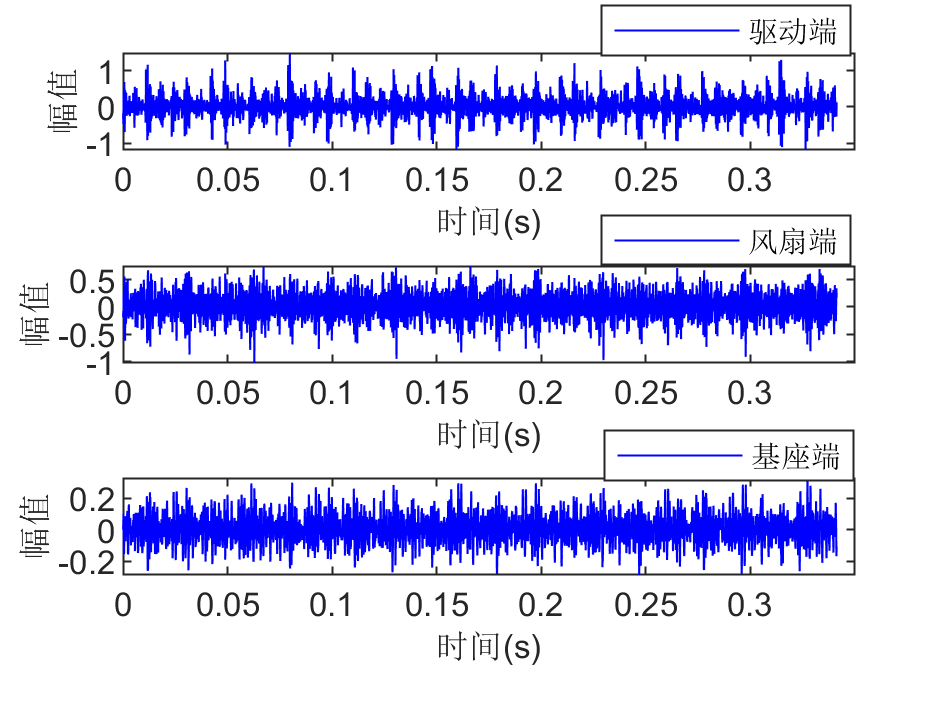
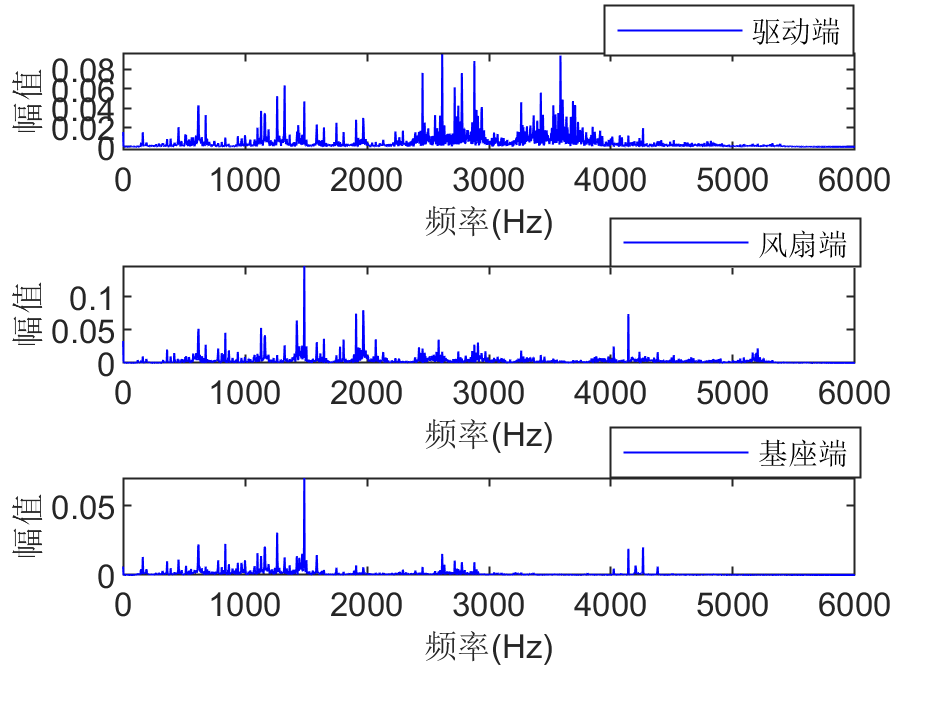
从图中能发现,不同位置处振动信号的时域波形在幅值上存在较大差异,在频域中风扇端和基座端的频谱分布较为相似,但幅值大小存在差异。
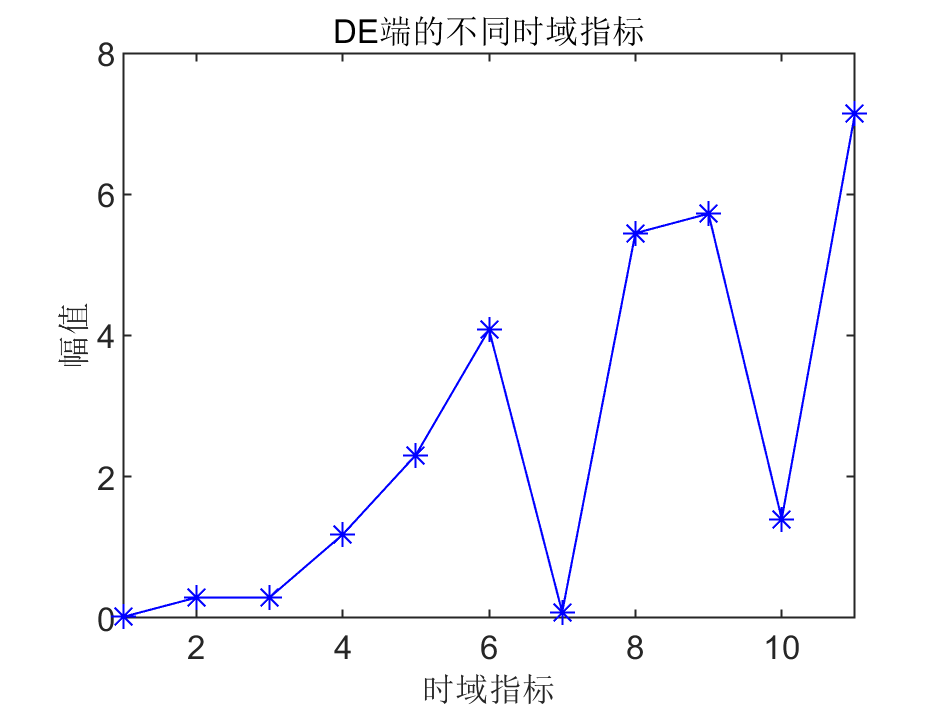
下图为驱动端某个样本11个时域指标的计算曲线:
在本例中,分别选择时域指标——峰峰值和频域指标——频率重心,分析不同位置处信号的差异,这里每个位置处长度为4096的信号被分成4个长度为1024的子信号进行分析,分别计算其不同指标,结果如下图所示:
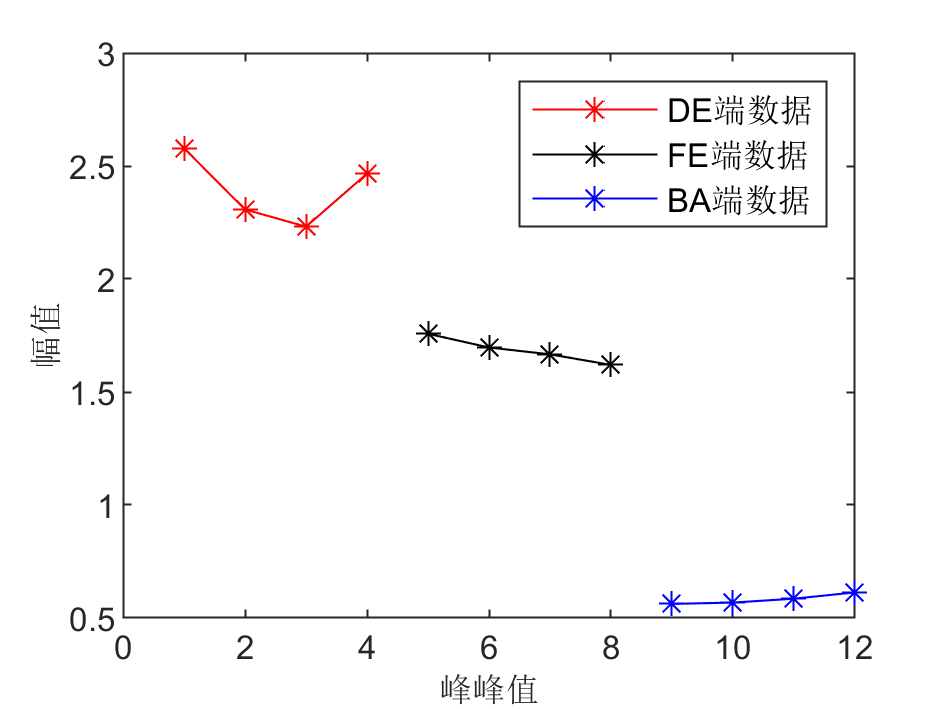
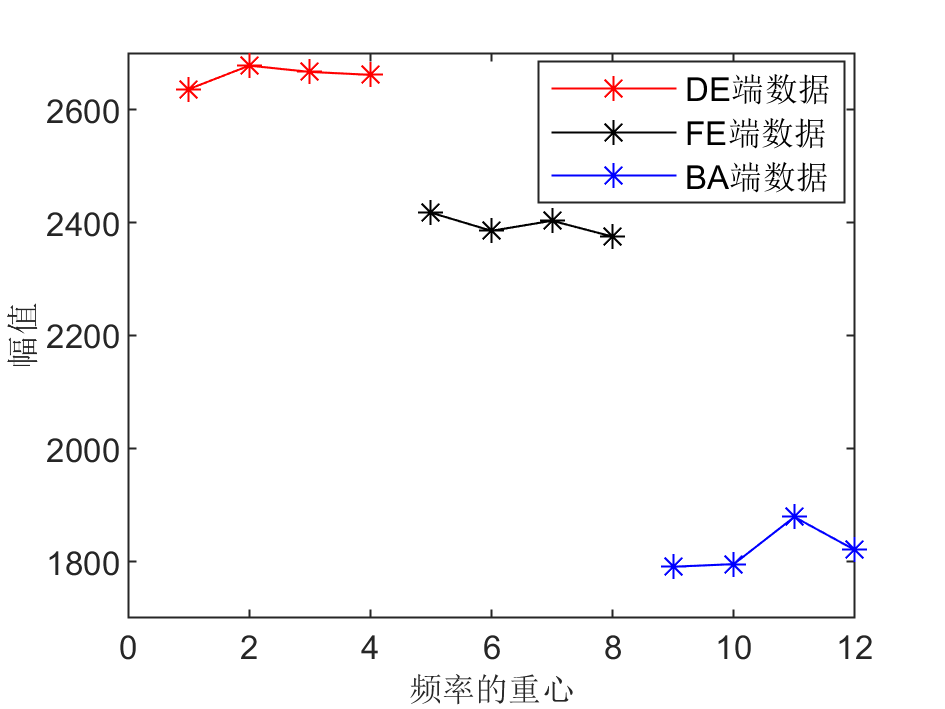
从图中能发现,不同位置处振动信号的峰峰值和频率重心存在较大差异,同一位置处的峰峰值和频率重心差异较小。因此,这些指标可用于判断信号的来源。
进一步分析不同位置处信号频域内频率重心(从上到小依次为驱动端、风扇端和基座端),结果下图所示
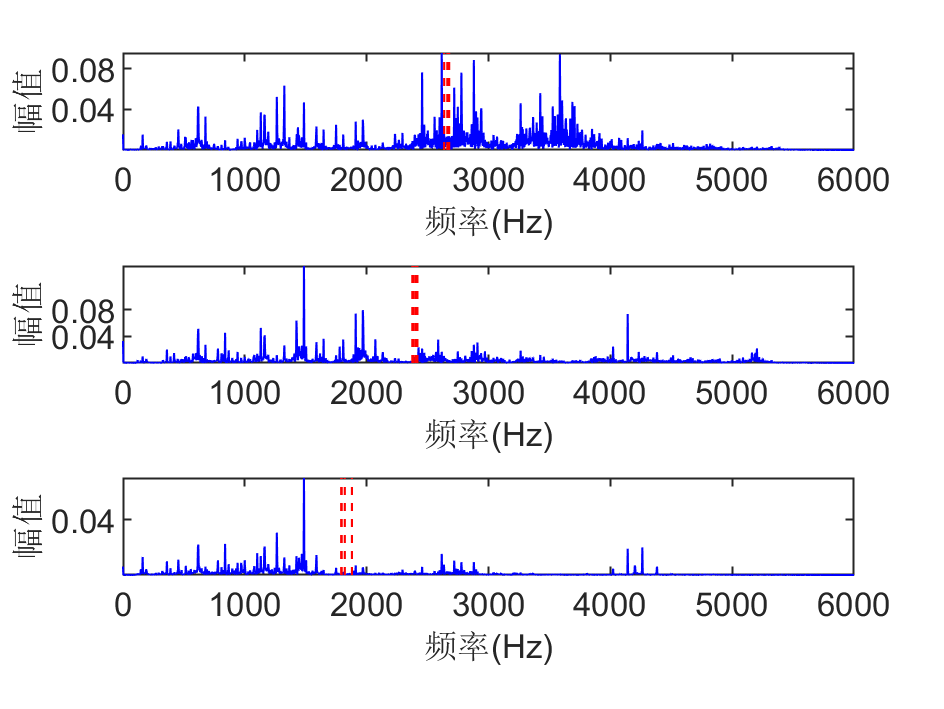
上图中,红色虚线分别为不同位置处4个子样本的频率重心位置。从图中能发现,在整个频域分析范围内,不同子样本频率重心差异小,不同位置处频率重心差异大。频率重心能直接地反映信号的主频带位置,但是也会受到无关分量的干扰而发生偏移,如风扇端和基座端的信号。
6、 代码分享
代码主要有4个(1个主程序、3个函数):
1、main.m(主函数:信号的时域和频域分析)
2、frequ_am_phase.m(幅值谱和相位谱计算函数)
调用形式:
[freq,P1,Theta]=frequ_am_phase(y,fs,tol)
输入:
y:所分析信号,矩阵,行X列=单个信号的采样索引X信号数,比如信号的大小为8192X12,表示一个有12个信号的数据矩阵,每个信号长度为8192。注意,如果仅有一个信号,则y应该是一个列向量。同时,y的行数尽量为偶数,奇数的话会引起程序索引的警告。
fs:采样频率,标量
tol:相位阈值参数,标量(可缺省)
输出
freq:表示幅值谱的横轴,向量,HzX1
P1:表示幅值谱的纵轴,矩阵,单个信号的采样索引X信号数,类比信号y
Theta:表示相位谱的纵轴,矩阵,单个信号的采样索引X信号数,类比信号y
3、GetTimeDomainFeature.m(时域指标计算函数)
调用形式:
SYPara=GetTimeDomainFeature(x)
输入:
x:所分析信号,矩阵,行X列=单个信号的采样索引X信号数,比如信号的大小为8192X12,表示一个有12个信号的数据矩阵,每个信号长度为8192。
输出:
SYPara:计算得到的时域统计特征参数(11×信号数,矩阵),比如11×10表示一个有10个信号的数据矩阵,每一列为该列信号的11个时域特征指标。
备注:
SYPara(1,:)-均值(MV);SYPara(2,:)-标准差(SD);SYPara(3,:)-均方根值(RMS);SYPara(4,:)-峰值(Peak);SYPara(5,:)-峰峰值(PPV);SYPara(6,:)-峰值因子(CRE);SYPara(7,:)-偏度(SKE);SYPara(8,:)-峭度(KUR);SYPara(9,:)-脉冲因子(IMP)SYPara(10,:)-波形因子(FOR); SYPara(11,:)-裕度因子(CLE);
4、GetFrequencyDomainFeature.m(频域指标计算函数)
调用形式:
Para=GetFrequencyDomainFeature(x,Fs)
输入:
x:所分析信号,矩阵,行X列=单个信号的采样索引X信号数,比如信号的大小为8192X12,表示一个有12个信号的数据矩阵,每个信号长度为8192。
Fs: 采样频率
输出:
Para:计算得到的频域统计特征参数(13×信号数,矩阵),比如13×10表示一个有10个信号的数据矩阵,每一列为该列信号的13个频域特征指标。
备注:
各个指标分别对应雷亚国老师的混合智能技术及其在故障诊断中的应用研究中表4-1。其中,Para(1,:)-频谱均值;Para(5,:)-频率重心;Para(7,:)-均方根频率;Para(13,:)-标准差频率;
1、main.m(主函数:信号的时域和频域分析)
%% 信号特征提取——常用时域和频域指标
%% 作者:冷漠
%% 时间:2024年8月19日
%% 关注公众号 :"故障诊断与寿命预测工具箱",每天进步一点点
clc
clear all
close all
%% 信号分析
load('105.mat')
f(:,1)=X105_DE_time(1001:1000+2^12,1)';
f(:,2)=X105_FE_time(1001:1000+2^12,1)';
f(:,3)=X105_BA_time(1001:1000+2^12,1)';
fs=12*10^3; %采样频率
L=size(f,1); %信号长度
t=(0:L-1)/fs; %时间序列
[freq,P1,~]=frequ_am_phase(f,fs); %幅值谱和相位谱 相位谱的阈值参数为1e-6
%时域波形
figure
subplot(311);plot(t,f(:,1),'b-');xlabel('时间(s)');ylabel('幅值');
subplot(312);plot(t,f(:,2),'b-');xlabel('时间(s)');ylabel('幅值');
subplot(313);plot(t,f(:,3),'b-');xlabel('时间(s)');ylabel('幅值');
%频域波形
figure
subplot(311);plot(freq,P1(:,1),'b-');xlabel('频率(Hz)');ylabel('幅值');
subplot(312);plot(freq,P1(:,2),'b-');xlabel('频率(Hz)');ylabel('幅值');
subplot(313);plot(freq,P1(:,3),'b-');xlabel('频率(Hz)');ylabel('幅值');
% 提取时域特征
feature_time_domain_all=[];
sub_count=4; %子样本的数量
for i=1:size(f,2)
sub_f=reshape(f(:,i),[],sub_count);
feature_time_domain=GetTimeDomainFeature(sub_f);
feature_time_domain_all=[feature_time_domain_all,feature_time_domain];
end
% 时域指标分析
figure;
plot(feature_time_domain_all(:,2),'b*-');xlabel('时域指标');ylabel('幅值');
title('DE端的不同时域指标')
%峰峰值
figure;
plot(1:sub_count,feature_time_domain_all(5,1:sub_count),'r-*');hold on;
plot(sub_count+1:2*sub_count,feature_time_domain_all(5,sub_count+1:2*sub_count),'k-*');
plot(2*sub_count+1:3*sub_count,feature_time_domain_all(5,2*sub_count+1:3*sub_count),'b-*');
xlabel('峰峰值');ylabel('幅值');
legend('DE端数据','FE端数据','BA端数据')
% 提取频域特征
feature_fre_domain_all=[];
sub_count=4; %子样本的数量
for i=1:size(f,2)
sub_f=reshape(f(:,i),[],sub_count);
feature_fre_domain=GetFrequencyDomainFeature(sub_f,fs);
feature_fre_domain_all=[feature_fre_domain_all,feature_fre_domain];
end
% 频率的重心对比
figure
plot(1:sub_count,feature_fre_domain_all(5,1:sub_count),'r-*');hold on;
plot(sub_count+1:2*sub_count,feature_fre_domain_all(5,sub_count+1:2*sub_count),'k-*');
plot(2*sub_count+1:3*sub_count,feature_fre_domain_all(5,2*sub_count+1:3*sub_count),'b-*');
xlabel('频率的重心');ylabel('幅值');
legend('DE端数据','FE端数据','BA端数据')
figure;
% DE端数据
subplot(311);plot(freq,P1(:,1),'b-');xlabel('频率(Hz)');ylabel('幅值');axis tight;hold on
ylimit = get(gca, 'YLim');
for i=1:1:sub_count
point=feature_fre_domain_all(5,i); %频率重心的位置
plot([point,point],ylimit,'r--');hold on;
end
% FE端数据
subplot(312);plot(freq,P1(:,2),'b-');xlabel('频率(Hz)');ylabel('幅值');axis tight;hold on
ylimit = get(gca, 'YLim');
for i=sub_count+1:2*sub_count
point=feature_fre_domain_all(5,i); %频率重心的位置
plot([point,point],ylimit,'r--');hold on;
end
% BA端数据
subplot(313);plot(freq,P1(:,3),'b-');xlabel('频率(Hz)');ylabel('幅值');axis tight;hold on
ylimit = get(gca, 'YLim');
for i=2*sub_count+1:3*sub_count
point=feature_fre_domain_all(5,i); %频率重心的位置
plot([point,point],ylimit,'r--');hold on;
end
2、frequ_am_phase.m(幅值谱和相位谱计算函数)
function [freq,P1,Theta]=frequ_am_phase(y,fs,tol)
%% 作者:冷漠
%% 时间:2024年6月01日
%% 关注公众号 :"故障诊断与寿命预测工具箱",每天进步一点点
%% 绘制信号频域的幅值谱和相位谱
%% 参数解释:
% y: 表示输入信号,它可以为一个矩阵,行X列,具体为单个信号的采样索引X信号数
% 比如y的大小为8192X12,表示一个有12个信号的数据矩阵,每个信号长度为8192
% 注意,如果仅有一个信号,则y应该是一个列向量
% 同时,y的行数尽量为偶数,奇数的话会引起程序索引的警告
% fs:表示采样频率
% tol:相位阈值参数
% freq:表示幅值谱的横轴
% P1:表示幅值谱的纵轴
% Theta:表示相位谱的纵轴
if nargin==2
tol=1e-6; %计算误差的默认阈值
end
L=size(y,1); % 信号长度
% Y=fft(y,2^nextpow2(L)); % FFT 快速傅里叶变换
Y=fft(y,L); % FFT 快速傅里叶变换
freq=(0:L/2)*fs/L; % 设置频率刻度 横轴Hz
%幅值谱
P2 = abs(Y/L);
P1 = P2(1:L/2+1,:);
P1(2:end-1,:) = 2*P1(2:end-1,:); %纵轴 幅值
%相位谱
P2(2:end-1,:)=2*P2(2:end-1,:);
for i=1:size(Y,2)
Y(P2(:,i)<tol,i) = 0;
theta(:,i) = angle(Y(:,i))/pi;
end
Theta=theta(1:L/2+1,:);
end3、GetTimeDomainFeature.m(时域指标计算函数)
function SYPara=GetTimeDomainFeature(x)
% GetTimeDomainFeature.m 函数:计算给定信号的时域统计特征值
% x 输入:所分析的信号,维度:行X列=单个信号的采样索引X信号数,
% 比如信号的大小为8192X12,表示一个有12个信号的数据矩阵,每个信号长度为8192
% SYPara 输出:计算得到的时域统计特征参数(11×信号数,矩阵)
% 比如11×10表示一个有10个信号的数据矩阵,每一列为该列信号的11个时域特征指标
% 具体的时域特征指标:
% SYPara(1,:)-均值(MV); SYPara(2,:)-标准差(SD);SYPara(3,:)-均方根值(RMS)
% SYPara(4,:)-峰值(Peak); SYPara(5,:)-峰峰值(PPV);SYPara(6,:)-峰值因子(CRE)
% SYPara(7,:)-偏度(SKE); SYPara(8,:)-峭度(KUR);SYPara(9,:)-脉冲因子(IMP)
% SYPara(10,:)-波形因子(FOR); SYPara(11,:)-裕度因子(CLE);
if nargin~=1
error('The Wrong Input');
end
%有量纲
MV=mean(x,1); %均值
SD=std(x,0,1); %标准差
RMS=sqrt(mean(x.^2,1)); %均方根值
Peak=max(abs(x),[],1); %峰值(Peak)
PPV=max(x,[],1)-min(x,[],1); %峰峰值(PPV)
%无量纲
CRE=Peak./RMS; %峰值因子
SKE=skewness(x,1,1); %偏度
KUR=kurtosis(x,1,1); %峭度
IMP=Peak./mean(abs(x),1); %脉冲因子
FOR=RMS./mean(abs(x),1); %波形因子
CLE=Peak./mean(sqrt(abs(x)),1).^2; %裕度因子
SYPara(1,:)=MV;SYPara(2,:)=SD;SYPara(3,:)=RMS;SYPara(4,:)=Peak;
SYPara(5,:)=PPV;SYPara(6,:)=CRE;SYPara(7,:)=SKE;SYPara(8,:)=KUR;
SYPara(9,:)=IMP;SYPara(10,:)=FOR;SYPara(11,:)=CLE;
end
4、GetFrequencyDomainFeature.m(频域指标计算函数)
function Para=GetFrequencyDomainFeature(x,Fs)
% GetFrequencyDomainFeature.m 函数:计算给定信号的频域统计特征值
% x 输入:要计算频域特征参数的信号,维度:行X列=单个信号的采样索引X信号数,
% 比如信号的大小为8192X12,表示一个有12个信号的数据矩阵,每个信号长度为8192
% Fs 输入:采样频率
% Para 输出:计算得到的频域统计特征参数(13×信号数,矩阵),
% 比如13×10表示一个有10个信号的数据矩阵,每一列为该列信号的13个频域特征指标。
T = 1/Fs; % Sampling period
L = size(x,1); % Length of signal
t = (0:L-1)*T; % Time vector
f_pin_yu=fft(x);
P2 = abs(f_pin_yu/L);
P1 = P2(1:L/2+1,:); %%频谱图纵坐标
P1(2:end-1,:) = 2*P1(2:end-1,:);
frequ = Fs*(0:(L/2))/L; %%频谱图的横坐标频率
N=size(P1,1); %频谱的长度
%频域指标
Para=zeros(13,size(x,2));
Para(1,:)=sum(P1,1)./N; %对应论文的P12 频谱均值
Para(2,:)=sum((P1-Para(1,:)).^2,1)./(N-1); %对应论文的P13
Para(3,:)=sum((P1-Para(1,1)).^3,1)./N./(sqrt(Para(2,:))).^3;%对应论文的P14
Para(4,:)=sum((P1-Para(1,1)).^4,1)./N./(Para(2,:).^2); %对应论文的P15
Para(5,:)=frequ*P1./sum(P1,1); %对应论文的P16 频率重心
Para(6,:)=sqrt(sum(P1.*(frequ-Para(5,:)')'.^2,1)./N); %对应论文的P17
Para(7,:)=sqrt(frequ.^2*P1./sum(P1,1)); %对应论文的P18 均方根频率
Para(8,:)=sqrt(frequ.^4*P1./(frequ.^2*P1)); %对应论文的P19
Para(9,:)=frequ.^2*P1./sqrt(sum(P1.*(frequ.^4*P1),1)); %对应论文的P20
Para(10,:)=Para(6,:)./Para(5,:); %对应论文的P21
Para(11,:)=sum(P1.*(frequ'-Para(5,:)).^3,1)./N./(Para(6,:)).^3;%对应论文的P22
Para(12,:)=sum(P1.*(frequ'-Para(5,:)).^4,1)./N./(Para(6,:)).^4;%对应论文的P23
Para(13,:)=sum(P1.*sqrt(abs(frequ'-Para(5,:))),1)./N./sqrt(Para(6,:));%对应论文的P24 标准差频率
end
7、细节说明
1、时域和频域指标可被用于分析不同信号的特点,具体用途读者自行尝试,本例只是为了给大家分享时域指标和频域指标计算函数,方便大家使用。
2、时域指标计算中,一些指标可用matlab的现成函数计算,顾不自行写具体计算过程代码。
3、频域指标计算过程中,根据公式,计算不同的频域指标。函数能同时计算若干个信号的频域指标,其中涉及到矩阵运算,来加速计算过程,欢迎各位读者推敲和指正。
8、总结
上述案例计算了不同信号的时域波形指标和频域波形指标,通过对比分析这些指标,可用于区分不同位置的振动信号,其中,常用的时域波形指标11个,频域波形指标13个。
为了更快速地计算各个特征指标,该代码实现了同时计算若干信号时域指标和频域指标,加速了信号的分析过程。
9、相关资料
vsqe
1、上述源码
①代码:
105.mat(数据文件)
main.m(主函数);
frequ_am_phase.m(幅值谱和相位谱计算函数)
GetTimeDomainFeature.m(时域指标计算函数)
GetFrequencyDomainFeature.m(频域指标计算函数)
2、相关参考
①雷亚国.混合智能技术及其在故障诊断中的应用研究[D].西安交通大学,2007.
②信号处理各项指标时域与频域指标https://zhuanlan.zhihu.com/p/621622520
③频域特征指标及其MATLAB代码实现(重心频率、均方频率、均方根频率、频率方差、频率标准差)https://zhuanlan.zhihu.com/p/425141767
更多内容,请关注公众号“故障诊断与寿命预测工具箱”,每天进步一点点。

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献11条内容
已为社区贡献11条内容







所有评论(0)