超详细的主动学习Active Learning介绍【理论+代码】
机器学习主要研究计算机如何利用经验数据提高自身性能。在监督学习中,数据的质量和数量直接决定模型的性能高低,监督学习不仅要求数据全部是标记好的,并且需要大量的数据,然而人工标注大量数据需要耗费巨大的时间和精力,一个更合理的方案是挑选一部分数据进行标注,这就要提到机器学习中的主动学习。
超详细的主动学习Active Learning介绍【理论+代码】
一、为什么要主动学习?
机器学习主要研究计算机如何利用经验数据提高自身性能。在监督学习中,数据的质量和数量直接决定模型的性能高低,监督学习不仅要求数据全部是标记好的,并且需要大量的数据,然而人工标注大量数据需要耗费巨大的时间和精力,一个更合理的方案是挑选一部分数据进行标注,这就要提到机器学习中的主动学习。
实际上,不同数据样本对于学习模型的贡献度不一样,过多的低质量数据反而会降低模型的鲁棒性,如果我们能够选取一部分最有价值的数据进行标注,就有可能仅基于少量数据就能获得同样高效的模型。实现这一目标的关键在于,如何选择出最有价值的数据样本并去获取它们的标记信息。
主动学习地目的是通过标记少量的数据训练处表现较好的模型。其核心任务是制定选择样本的标准,从而选择尽可能少的样本进行标注来选出一个好的学习模型。
二、主动学习的应用场景
1.基于数据池的主动学习
是最常见的一种场景,给定未标记的样本数据池,通过算法每次从未标记数据池中选择最具代表性的样本,交给标注者标注,然后向训练集中添加这些新的样本更新训练集,基于新训练集继续更新模型,进入下一次迭代。
2.基于数据流的主动学习
基于数据流的主动学习将未标记的数据逐一通过选择算法决定是否需要标注当前样本,若不选择则丢弃样本。该场景适用于数据量较大且数据源是流式而又无法保存下来所有数据的情况。
3.基于合成样本查询的主动学习
基于合成样本查询的主动学习并不是从已有的样本中选择来查询标记信息,而是直接从特征空间里合成出新的样本进行查询。这种方法可以解决标记数据难以获得的问题,但是由于新和成的样本可能是特征空间里任意取值组合产生的,因此在某些应用问题中可能导致人类专家也无法标注这些合成样本。例如在图像分类任务中,任意像素取值合成的图片可能并不能呈现清晰的语义,因此合成样本的质量和真实性可能会对算法的效果产生影响。
三、主动学习的流程
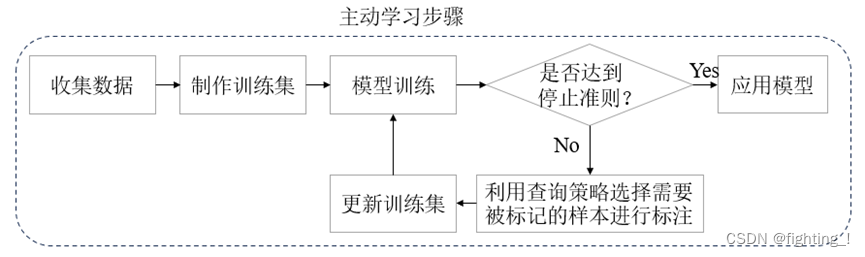
1.主动学习的步骤
主动学习的步骤如下图所示:

1)首先在未标记的数据集中选取少量样本进行标注,构成训练集;
2)选取训练模型,使用少量标注样本的训练集对模型进行训练,此时模型的性能不高;
3)使用训练好的模型预测未标注的样本;
4)定义查询策略(包括度量预测的不确定度以及应用于请求标注的查询策略),根据策略返回未标注样本的优先级评分,选择出的需要标注的数据,进行人工标注;
5)将新选择的数据加入到训练集中更新训练集,使用更新后的训练集来训练模型;
6)判断模型是否达到停止准则?若未达到停止标准,则继续利用查询策略选择需要被标记的样本并进行人工标注,循环第4-5-6步,直到达到停止标准(这个准则可以是迭代次数,也可以是准确率等指标达到设定值例如模型精度超过99%),表示模型已训练好可以应用。
2.主动学习的模型
主动学习算法模型定义为:A= (C, L, S, Q, U);其中C为一个或一组分类器(当有多个模型时,可使用集成模型),L为已标注的训练样本集,U为整个未标注样本集,S为督导者,对U中未标注样本进行标注,Q为查询函数,用于在U中查询信息量大的样本。

3.常用查询策略
查询策略(Query Strategy Frameworks)是主动学习的核心之处:按照什么准则来选择被查询的样本?目前的方法分为三种:基于信息量的查询策略、基于代表性的查询策略和综合多种准则的查询策略。
- 基于信息量的查询策略
最常见的一种,基本思想是选择那些能最大限度减小当前模型不确定性的样本进行查询。具体而言,信息量又可以通过模型预测的置信度、模型错误率下降期望、委员会投票等多种形式进行度量。这类方法选择样本时只基于现有的已标记样本,忽略了大量的未标记样本中蕴含的数据分部信息,可能导采样偏差问题。
- 基于代表性的查询策略
倾向于选择那些更能刻画数据整体分布的未标记数据进行标记查询。这些方法往往通过聚类或密度估计等无监督技术来评估样本的代表性,由于忽略了已标记样本因此整体性能也可能会依赖于聚类结果的好坏。
- 综合多种准则的查询策略
能够同时考虑选择样本的信息量和代表性,能够有效避免采样偏差和依赖聚类结果的问题。近年来已有研究者从不同角度提出综合多种查询准则的主动学习方法,并展示出较好的实验性能。
这里给出最常用的不确定性度量的查询策略:
(1)不确定性采样的查询
① 最小置信度(Least confidence)
选择那些最大概率最小的样本进行标注。即对于每个数据点的选择概率的最大值从小到大进行排序。用公式表示就是:


其中, y ^ \hat{y} y^对x而言是模型预测概率最大的类别, P θ ( y ^ │ x ) \ P_\theta (\hat{y}│x) Pθ(y^│x)指的是最大概率的类别对应的概率。举例:假设两个样本预测结果如下:
| Data | Class1 | Class2 |
|---|---|---|
| x1 | 0.9 | 0.1 |
| x2 | 0.58 | 0.42 |
那么第一样本预测概率最大的类别是Class1,概率为0.9,第二个样本预测概率最大的类别是Class1,概率为0.58,这时0.58<0.9,因此第二个样本更“难”被区分,因此更有被继续标注的价值。再如:
| Data | Class1 | Class2 | Class3 |
|---|---|---|---|
| x1 | 0.9 | 0.05 | 0.05 |
| x2 | 0.58 | 0.22 | 0.2 |
| x3 | 0.2 | 0.6 | 0.2 |
| x4 | 0.1 | 0.1 | 0.8 |
那么第一个样本预测概率最大的类别是Class1,概率为0.9,第二个样本预测概率最大的类别是Class1,概率为0.58,第三个样本预测概率最大的类别是Class2,概率为0.6,第四个样本预测概率最大的类别是Class3,概率是0.8,此时0.58<0.6<0.8<0.9,因此第二个样本更 “难”被区分,更有被继续标注的价值。
最小置信度方法考虑那些模型预测概率最大但是可信度较低的样本数据。是最简单,最常用的方法,它通过置信度排序以最低的置信度对其预测的样本进行采样。
② 边际抽样(Margin Sampling)
该方法与最小置信度法类似,不同在于该方法考虑最大概率和第二大概率的差异。边际抽样选择那些极容易被判定成两类的样本数据,这些数据被判定成两类的概率相差不大,即选择模型预测最大和第二大的概率差值最小的样本。公式表示为:

其中
y
^
1
\hat{y}_1
y^1和
y
^
2
\hat{y}_2
y^2对x而言分别是模型预测概率最大的类别和第二大可能的类别。举例:
| Data | Class1 | Class2 | Class3 |
|---|---|---|---|
| x1 | 0.9 | 0.05 | 0.05 |
| x2 | 0.58 | 0.22 | 0.2 |
| x3 | 0.2 | 0.6 | 0.2 |
| x4 | 0.05 | 0.15 | 0.8 |
那么第一个样本预测为最大可能的类别为Class1,概率为0.9,第二大可能的类别为Class2/ Class3,概率为0.05,因此最大可能类别与第二大可能类别的概率差为0.9-0.05=0.85,同样地第二个样本的概率差为0.58-0.22=0.36,第三个样本的概率差为0.6-0.2=0.4,第四个样本的概率差为0.8-0.15=0.65,优先级排序为0.36<0.4<0.65<0.85,因此第二个样本更 “难”被区分,更有被继续标注的价值。
边际抽样得分较低的数据点是被标记为最可能类的点;同时是模型在最可能的类别和第二个最可能的类别之间不确定的数据点。
③ 熵(Entropy)
熵指的是系统的混乱程度或无序程度。熵越大反映系统不确定性越大。因此,选择熵大的样本进行标注有利于提升模型性能。基于熵选取样本的公式如下:

该方法考虑了模型对某个样本的所有类别判定的结果。举例:
| Data | Class1 | Class2 | Class3 |
|---|---|---|---|
| x1 | 0.9 | 0.05 | 0.05 |
| x2 | 0.58 | 0.22 | 0.2 |
| x3 | 0.2 | 0.6 | 0.2 |
| x4 | 0.05 | 0.15 | 0.8 |
对于第一个样本-0.9ln0.9-0.05ln0.05-0.05ln0.05=0.394,对于第二个样本-0.58ln0.58-0.22ln0.22-0.2ln0.2=0.97,对于第三个样本-0.2ln0.2-0.6ln0.6-0.2ln0.2=0.95,对于第四个样本-0.05ln0.05-0.15ln0.15-0.8ln0.8=0.613,优先级排序0.97>0.95>0.613>0.394,因此第二个样本更 “难”被区分,更有被继续标注的价值。
(2)基于委员会的查询(Query-By-Commitee)
不确定性采样的查询策略只使用单个模型,基于委员会的查询考虑多个模型。类似于集成学习。它通过多个模型进行投票的方式选择出较为难区分的数据。包括两个步骤:首先使用多个模型构成委员会;然后委员会中所有模型对所有未标记样本进行预测,筛选出投票最不一致的样本进行标注。
① 投票熵(Vote Entropy)
当多个模型将样本都投票为某一类,代表该样本容易区分,当多个模型对某个样本的投票结果都不一致时,代表带样本难以区分,需要重点关注。这种场景下可以用熵来衡量数据被多个模型投票的难易程度,数学公式表达如下:

其中,
y
i
{y}_i
yi表示第i类,V(
y
i
{y}_i
yi)表示样本被投票为
y
i
{y}_i
yi类的模型数,C表示模型总数,且
∑
i
V
(
y
i
)
=
C
\sum_iV({y}_i)=C
∑iV(yi)=C。
② 平均KL散度(Average KL Divergence)
KL散度可以衡量两个概率分布之间的“距离”,也就是两个概率分布之间的相似程度,因此可以使用KL散度计算出偏差较大的数据样本。数学公式表达如下:

其中
P
c
(
y
i
∣
x
)
=
1
C
∑
c
=
1
C
P
θ
(
y
i
∣
x
)
P_c(y_i|x)=\frac{1}{C}\sum_{c=1}^CP_\theta(y_i|x)
Pc(yi∣x)=C1∑c=1CPθ(yi∣x)也是概率分布,
D
(
P
θ
(
c
)
∣
∣
P
C
)
=
∑
i
P
θ
(
c
)
(
i
)
log
P
C
(
i
)
P
θ
(
c
)
(
i
)
D(P_{\theta^(c)}||P_C)=\sum_i{P_{\theta^(c)}(i)}\log_{P_C(i)}^{P_{\theta^(c)}(i)}
D(Pθ(c)∣∣PC)=∑iPθ(c)(i)logPC(i)Pθ(c)(i)表示两个概率分布的KL散度。
(3)模型变化期望(Expected Model Change)
模型错误率下降越多证明模型越好,让模型变化最大可以选择使得梯度变化最大的样本数据。
(4)基于误差减少的查询
选择那些通过增加一个样本就使得 loss函数减少最多的样本数据。
(5)基于方差减少的查询
选择方差降低最多的样本数据。
(6)基于密度权重减少的查询
当数据分布不均匀时,某个数据可能位于稀疏区或者是异常点,不太适合作为主动学习标注的样本,或者数据具有明显的聚类结构,即不同类别的数据点在特征空间中有较大的区分度时,使用密度权重可以更准确地反映数据点的重要性和捕捉聚类这样的结构。这时考虑那些稠密的较难区分的数据点价值更大。公式为:

其中,
Θ
A
\Theta_A
ΘA表示不确定性采样方法或基于委员会查询的方法,
β
\beta
β表示指数参数,
x
(
u
)
x^{(u)}
x(u)表示第u类的代表元,𝑈表示类别数。加上权重表示会选择那些与代表元相似度较高的元素作为标注候选集。
四、主动学习的代码
1.举例:回归任务(使用不确定性采样的查询策略)
首先导入需要的包
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import WhiteKernel, RBF
from modAL.models import ActiveLearner
然后定义数据
# 生成回归数据集
X = np.random.choice(np.linspace(0, 20, 10000), size=200, replace=False).reshape(-1, 1)
y = np.sin(X) + np.random.normal(scale=0.3, size=X.shape)
对原始数据可视化
with plt.style.context('seaborn-white'):
plt.figure(figsize=(10, 5))
plt.scatter(X, y, c='k', s=20)
plt.title('sin(x) + noise')
plt.show()

对初始数据进行选择
n_initial = 5 # 最开始随机选取5个标注好的数据集进行训练
initial_idx = np.random.choice(range(len(X)), size=n_initial, replace=False)
X_training, y_training = X[initial_idx], y[initial_idx]
定义查询策略
def GP_regression_std(regressor, X):
_, std = regressor.predict(X, return_std=True) # 不确定度度量
query_idx = np.argmax(std) # 样本的选取
return query_idx, X[query_idx]
定义高斯模型核函数
kernel = RBF(length_scale=1.0, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(noise_level=1, noise_level_bounds=(1e-10, 1e+1))
定义ActiveLearner
regressor = ActiveLearner(
estimator=GaussianProcessRegressor(kernel=kernel),
query_strategy=GP_regression_std,
X_training=X_training.reshape(-1, 1), y_training=y_training.reshape(-1, 1)
)
对初始模型结果进行可视化
X_grid = np.linspace(0, 20, 1000)
y_pred, y_std = regressor.predict(X_grid.reshape(-1, 1), return_std=True)
y_pred, y_std = y_pred.ravel(), y_std.ravel()
with plt.style.context('seaborn-white'):
plt.figure(figsize=(10, 5))
plt.plot(X_grid, y_pred)
plt.fill_between(X_grid, y_pred - y_std, y_pred + y_std, alpha=0.2)
plt.scatter(X, y, c='k', s=20)
plt.title('Initial prediction')
plt.show()

定义待标记样本数并进行模型迭代
n_queries = 10
for idx in range(n_queries):
query_idx, query_instance = regressor.query(X)
regressor.teach(X[query_idx].reshape(1, -1), y[query_idx].reshape(1, -1))
y_pred_final, y_std_final = regressor.predict(X_grid.reshape(-1, 1), return_std=True)
y_pred_final, y_std_final = y_pred_final.ravel(), y_std_final.ravel()
可视化最终结果:
with plt.style.context('seaborn-white'):
plt.figure(figsize=(10, 8))
plt.plot(X_grid, y_pred_final)
plt.fill_between(X_grid, y_pred_final - y_std_final, y_pred_final + y_std_final, alpha=0.2)
plt.scatter(X, y, c='k', s=20)
plt.title('Prediction after active learning')
plt.show()

2.举例:分类任务(使用基于委员会的查询)
导入需要的包
from copy import deepcopy
import matplotlib.pyplot as plt
import numpy as np
from modAL.models import ActiveLearner, Committee
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier
加载数据集并对不同类别可视化
# loading the iris dataset
iris = load_iris()
# visualizing the classes
with plt.style.context('seaborn-white'):
plt.figure(figsize=(7, 7))
pca = PCA(n_components=2).fit_transform(iris['data'])
plt.scatter(x=pca[:, 0], y=pca[:, 1], c=iris['target'], cmap='viridis', s=50)
plt.title('The iris dataset')
plt.show()

生成数据池
X_pool = deepcopy(iris['data'])
y_pool = deepcopy(iris['target'])
初始化委员会成员
n_members = 2
learner_list = list()
for member_idx in range(n_members):
# initial training data
n_initial = 5
train_idx = np.random.choice(range(X_pool.shape[0]), size=n_initial, replace=False)
X_train = X_pool[train_idx]
y_train = y_pool[train_idx]
# creating a reduced copy of the data with the known instances removed
X_pool = np.delete(X_pool, train_idx, axis=0)
y_pool = np.delete(y_pool, train_idx)
# initializing learner
learner = ActiveLearner(
estimator=RandomForestClassifier(),
X_training=X_train, y_training=y_train
)
learner_list.append(learner)
构成委员会
committee = Committee(learner_list=learner_list)
可视化初始预测结果:
# visualizing the initial predictions
with plt.style.context('seaborn-white'):
plt.figure(figsize=(7, 7))
prediction = committee.predict(iris['data'])
plt.scatter(x=pca[:, 0], y=pca[:, 1], c=prediction, cmap='viridis', s=50)
plt.title('Committee initial predictions, accuracy = %1.3f' % committee.score(iris['data'], iris['target']))
plt.show()

定义待标记样本数并进行迭代
# query by committee
n_queries = 10
for idx in range(n_queries):
query_idx, query_instance = committee.query(X_pool)
committee.teach(
X=X_pool[query_idx].reshape(1, -1),
y=y_pool[query_idx].reshape(1, )
)
# remove queried instance from pool
X_pool = np.delete(X_pool, query_idx, axis=0)
y_pool = np.delete(y_pool, query_idx)
可视化最终结果
with plt.style.context('seaborn-white'):
plt.figure(figsize=(7, 7))
prediction = committee.predict(iris['data'])
plt.scatter(x=pca[:, 0], y=pca[:, 1], c=prediction, cmap='viridis', s=50)
plt.title('Committee predictions after %d queries, accuracy = %1.3f'
% (n_queries, committee.score(iris['data'], iris['target'])))
plt.show()

五、ModAL库和ALiPy库的官方文档与代码
ModAL库官网:https://modal-python.readthedocs.io/en/latest/index.html
ModAL库代码:https://github.com/modAL-python/modAL
ALiPy库官网:http://parnec.nuaa.edu.cn/huangsj/alipy/
ALiPy库代码:https://github.com/NUAA-AL/ALiPy
查阅了很多其他博主的博客后进行了总结与理解,再次感谢各位
1.机器学习中的主动学习
2.人工智能之机器学习篇——主动学习
3.主动学习的基本过程
4.计算机视觉中的主动学习(Active Learning)介绍
5.主动学习 (Active learning) 综述
6.主动学习(Active Learning,AL)综述
7.Active Learning 主动学习
8.主动学习框架
9.主动学习(Active Learning,AL)的理解以及代码流程讲解
10.深度学习 神经网络 人工智能 PYTHON 主动学习(ACTIVE LEARNING,AL)的理解以及代码流程讲解

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容





所有评论(0)