GBDT 梯度提升树（Gradient Boosting Decision Tree）长篇全解

GBDT梯度提升树

Wing以一

7409人浏览 · 2022-11-21 12:02:07

Wing以一 · 2022-11-21 12:02:07 发布

【参考视频】

1、视频课程：【技术干货】集成算法专题：梯度提升树GBDT（2022新版）_哔哩哔哩_bilibili

2、原理书籍：李航老师的《统计学习》第8章，相关讲解视频：8.提升方法_哔哩哔哩_bilibili

3、可参考的其它博客：梯度提升树(GBDT)原理小结 - 刘建平Pinard - 博客园 (cnblogs.com)

（1）n_estimators（迭代次数）

（2）learning_rate（学习率参数）

(3) init (输入计算初始预测结果编辑的估计器对象)

（4）属性init_ (模型被拟合完毕之后，返回输出编辑的评估器对象)

2、分类任务涉及的参数

(5) 属性n_estimators_ （实际迭代次数）

(6) 属性estimators_ （实际建立的弱评估器数量）

3、损失函数涉及的参数

（7）loss （损失函数）

(8)alpha (选取huber为损失函数时的阈值/选取quantile为损失函数时用以辅助计算输出结果，默认0.9）

损失函数的选择：

（9）属性loss_（返回具体的损失函数对象，而不会返回公式）

4、弱评估器结构相关的参数及属性

（10）max_depth：弱评估器被允许的最大深度

（11）min_samples_split：弱评估器分枝时，父节点上最少要拥有的样本个数

（12）min_samples_leaf：弱评估器的叶子节点上最少要拥有的样本个数

（14）min_weight_fraction_leaf：叶子节点所需最小权重和

（15）max_leaf_nodes：弱评估器上最多可以有的叶子节点数量

（16）min_impurity_decrease：弱评估器分枝时允许的最小不纯度下降量

（17）criterion：弱评估器分枝时的不纯度衡量指标

5、与提前停止问题相关的参数

（18）validation_fraction（验证集占比）

（19）n_iter_no_change（多少次下降无效则停止迭代）

（20）tol（损失函数下降的阈值）

6、和随机提升树相关的参数

（21）subsample (对数据的随机有放回抽样比例)

（22）max_features（对特征的有放回抽样比例由参数）

（23）random_state（随机数种子）

（24）属性oob_improvement_ （袋外分数的变化值）

（25）属性 train_score_（袋内分数的变化值）

一、相关基础知识

Boosting三要素：

损失函数 $L(x,y)$ ：用以衡量模型预测结果与真实结果的差异
弱评估器 $f(x)$ ：（一般为）决策树，不同的boosting算法使用不同的建树过程
综合集成结果 $H(x)$ ：即集成算法具体如何输出集成结果

Boosting算法的基本建模流程：

依据上一个弱评估器 $f(x)_{t-1}$ 的结果，计算损失函数 $L(x,y)$
使用 $L(x,y)$ 自适应地影响下一个弱评估器 $f(x)_t$ 的构建
集成模型输出的结果，受到整体所有弱评估器 $f(x)_0$ ~ $f(x)_T$ 的影响

拟合残差：每次用于建立弱评估器的是样本 $X$ 以及当下集成输出 $H(x_i)$ 与真实标签 $y$ 的差异（ $y - H(x_i)$ ）。这个差异在数学上被称之为残差（Residual），因此GBDT不修改样本权重，而是通过拟合残差来影响后续弱评估器结构。

二、调用sklearn实现GBDT

sklearn当中集成了GBDT分类与GBDT回归，我们使用如下两个类来调用它们：

(可查看scikitlearn官网：1.11. Ensemble methods — scikit-learn 1.1.3 documentation

1、梯度提升回归树

#梯度提升回归树
gbr = GBR(random_state=1024)    #模型实例化
result_gbdt = cross_validate(gbr, X, y, cv=cv
                             ,scoring="neg_root_mean_squared_error"  #评估指标：负根均方误差
                             ,return_train_score=True   #是否返回训练分数
                             ,verbose=True  #是否打印建模流程
                             ,n_jobs=-1)    #调用全部cpu来运行
print(RMSE(result_gbdt,"train_score"))
print(RMSE(result_gbdt,"test_score"))

2、梯度提升分类树

#梯度提升分类数
clf = GBC(random_state=1024)    #实例化
cv = KFold(n_splits=5,shuffle=True,random_state=1024)
result_clf = cross_validate(clf,X_clf,y_clf,cv=cv
                            ,return_train_score=True
                            ,verbose=True
                            ,n_jobs=-1)
print(result_clf)
print(result_clf["train_score"].mean())     ##均方根误差de另一种写法
print(result_clf["test_score"].mean())

三、参数&属性详解

1、迭代过程涉及的参数

（1）n_estimators（迭代次数）

=100，默认迭代100次

（2）learning_rate（学习率参数）

=0.1，默认学习率为0.1

对于样本 $x_i$ ，集成算法当中一共有 $T$ 棵树，则参数`n_estimators`的取值为 $T$ 。假设现在正在建立第 $t$ 个弱评估器，则则第 $t$ 个弱评估器上 $x_i$ 的结果可以表示为 $f_t(x_i)$ 。假设整个Boosting算法对样本 $x_i$ 输出的结果为 $H(x_i)$ ，则该结果一般可以被表示为 $t$ =1~ $t$ = $T$ 过程当中，所有弱评估器结果的加权求和：

$H(x_i) = \sum_{t=1}^{T}\phi _{t}f_{t}(x_{i})$

$\phi_t$ 为第t棵树的权重。对于第 $t$ 次迭代来说，则有：

$H_t(x_i) = H_{t-1}(x_i) + {\color{blue}\phi_t}f_t(x_i)$

每次将本轮建好的决策树加入之前的建树结果时，可以在权重 $\phi$ 前面增加参数 $\eta$ ，表示为第t棵树加入整体集成算法时的学习率，对标参数`learning_rate`。

$H_t(x_i) = H_{t-1}(x_i) + \boldsymbol{\color{red}\eta} \phi_tf_t(x_i)$

学习率很大时， $H(x_i)$ 增长得更快，所需的`n_estimators`更少;

当学习率较小时， $H(x_i)$ 增长较慢，所需的`n_estimators`就更多

因此boosting算法往往会需要在`n_estimators`与`learning_rate`中做出权衡。

(3) init (输入计算初始预测结果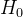 $H_0$ 的估计器对象)

可以输入任意评估器、字符串"zero"、或者None对象，默认为None对象。

建立第一个弱评估器时有： $H_1(x_i) = H_{0}(x_i) + \phi_1f_1(x_i)$

由于没有第0棵树的存在，因此 $H_0(x_i)$ 的值在数学过程及算法具体实现过程中都需要进行单独的确定，这一确定过程由参数`init`确定。

当输入任意评估器时，评估器必须要具备fit以及predict_proba功能，可以使用决策树、逻辑回归等可以输出概率的模型。如果输出一个已经训练过、且精细化调参后的模型,将会使得GBDT产生更好的效果。
填写为字符串"zero"，则代表令 $H_0 = 0$ 来开始迭代。（稳妥的做法，但一般不会得到较好的结果）
不填写，或填写为None对象，sklearn则会自动选择类`DummyEstimator`中的某种默认方式进行预测作为 $H_0$ 的结果

（4）属性init_ (模型被拟合完毕之后，返回输出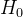 $H_0$ 的评估器对象)

一般用于在建模过程中进行监控打印时、或在大量初始化模型中选择最佳初始化模型时。

实验对比不同的init对最终结果的影响：

tree_reg = DTR(random_state=1409)  #决策树
rf = RFR(n_estimators=89, max_depth=22, max_features=14, min_impurity_decrease=0
              ,random_state=1409, verbose=False, n_jobs=-1)     #随机森林
for init in[tree_reg, rf, "zero", None]:
    reg = GBR(init = init, random_state=1409)
    cv = KFold(n_splits=5, shuffle=True, random_state=1409)
    result_reg = cross_validate(reg,X,y,cv=cv,scoring="neg_root_mean_squared_error"
                                ,return_train_score=True
                                ,verbose=False
                                ,n_jobs=-1)
    print("\n")
    print("init=",init)
    print(RMSE(result_reg, "train_score"))
    print(RMSE(result_reg, "test_score"))

2、分类任务涉及的参数

(5) 属性n_estimators_ （实际迭代次数）

(6) 属性estimators_ （实际建立的弱评估器数量）

GBDT与AdaBoost及随机森林的关键区别之一，是GBDT中所有的弱评估器都是回归树，因此在实际调用梯度提升树完成分类任务时，需要softmax函数或sigmoid函数对回归树输出的结果进行处理。

二分类问题：

$H(x_i) = \sum_{t=1}^T\phi_tf_t(x_i)$

$p(\hat{y}_i = 1 |x_i) = \sigma(H(x_i))$

其中 $\sigma$ 是sigmoid函数，当 $p(\hat{y}_i = 1 |x_i)$ 大于0.5时，样本 $x_i$ 的预测类别为1，反之则为0。

多分类问题：

GBDT对于多分类也只能输出集成算法回归结果 $H(x_i)$ ，因此需要使用softmax函数将回归值转化为概率，而Softmax函数是接受K个连续型结果，并输出K个相对概率的函数。

$K$ 分类、且每个类别为[1,2,3...k]时，我们则分别按照y = 1, y = 2,...,y = k进行建模，总共建立K棵树，每棵树输出的结果为：

$H^1(x_i), H^2(x_i),...,H^k(x_i)$

总共K个输出结果。然后，我们分别将 $H^1(x_i)$ 到 $H^k(x_i)$ 的结果输入softmax，来计算出每个标签类别所对应的概率。具体地来说，softmax函数的表达式为：

$Softmax(H^k(x)) = \frac{e^{H^k(x)}}{\sum_{k=1}^Ke^{H_k(x)}}$

其中e为自然常数，H是集成算法的输出结果，K表示标签中的类别总数为 $K$ ， $k$ 表示任意标签类别， $H_k$ 则表示以类别 $k$ 为真实标签进行训练而得出的H。

softmax函数的分子时多分类状况下某一个标签类别的H(x)的指数函数，分母时多分类状况下所有标签类别的H(x)的指数函数之和，因此Softmax函数的结果代表了样本的预测标签为类别k的概率。

三分类[1,2,3]，则样本i被分类为1类的概率为：

$p^1(x_i) = \frac{e^{H^1(x)}}{\sum_{k=1}^Ke^{H_k(x)}} = \frac{e^{H^1(x)}}{e^{H^1(x)}+e^{H^2(x)}+e^{H^3(x)}}$

最终得到K个相对概率 $p^k(x_i)$ ，并求解出相对概率最高的类别。

在执行多分类任务时，如果要求模型迭代10次，模型则会按照实际的多分类标签数n_classes建立10 * n_classes个弱评估器。可以通过属性n_estimators_以及属性estimators_查看到。

clf = GBC(n_estimators=10   #迭代次数为10次
          ,random_state=1409)
clf = clf.fit(X_clf,y_clf)
print(clf.n_estimators_)    #实际迭代数量为10
print(clf.estimators_.shape)
print(clf.estimators_[0])

多分类计算繁琐的问题一般只在弱评估器为回归器的各类boosting算法中出现。

3、损失函数涉及的参数

（7）loss （损失函数）

A：对于梯度提升分类树来说，loss的备选项有：

分类器中的loss：字符串型，可输入{"deviance", "exponential"}，默认值="deviance"

"deviance"（偏差），特指逻辑回归的损失函数——交叉熵损失函数
"exponential"特指AdaBoost中使用的指数损失函数

对任意样本i而言， $y_i$ 为真实标签， $\hat{y_i}$ 为预测标签， $H(x_i)$ 为集成算法输出结果， $p(x_i)$ 为基于 $H(x_i)$ 和sigmoid/softmax函数计算的概率值。

loss = "deviance"时：

如果是二分类交叉熵损失函数为： $L = -\left( y\log p(x) + (1 - y)\log(1 - p(x)) \right)$

（注意区分：对于GBDT来说 $p(x_i) = Sigmoid(H(x_i))$ ；而之前的逻辑回归 $p = H(x)$ ）

如果是多分类交叉熵损失函数为： $L = -\sum_{k=1}^Ky^*_k\log(P^k(x))$

$P^k(x)$ 是概率值，对于多分类GBDT来说， $p^k(x) = Softmax(H^k(x))$ 。 $y^*$ 是由真实标签转化后的向量。在3分类情况下，真实标签 $y_i$ 为2时， $y^*$ 为[ $y^*_{1}$ , $y^*_{2}$ , $y^*_{3}$ ]，取值分别为：[0,1,0]。

loss = "exponential"时：

如果是二分类指数损失函数为： $L = e^{-yH(x)}$
如果是多分类指数损失函数为： $L =e^{ -\frac{1}{K}y^{*}\cdot H^{*}(x)} = e^{ -\frac{1}{K}(y^1H^1(x)+y^2H^2(x) \ + \ ... + y^kH^k(x))}$

（指数损失中的 $y^*$ 与交叉熵损失中的 $y^*$ 不是同样的向量）

一般梯度提升分类器默认使用交叉熵损失，(即设置loss="deviance"）如果使用指数损失，则相当于执行没有权重调整的AdaBoost算法。

B：对于梯度提升回归树来说，loss的备选项有：

回归器中的loss：字符串型，可输入{"squared_error", "absolute_error", "huber", "quantile"}，默认值="squared_error"

'squared_error'是指回归的平方误差，'absolute_error'指的是回归的绝对误差，这是一个鲁棒的损失函数。'huber'是以上两者的结合。'quantile'则表示使用分位数回归中的弹球损失pinball_loss。

对任意样本i而言， $y_i$ 为真实标签， $H(x_i)$ 为预测标签（回归类问题中 $H(x_i)$ 不需要转化），则各个损失的表达式为：

squared_error： $L = \sum{(y_i - H(x_i))^2}$
absolute_error： $L = \sum{|y_i - H(x_i)|}$
huber： $L = \sum{l(y_i,H(x_i))}$ $l =\left\{\begin{matrix} \frac{1}{2}(y_i - H(x_i))^2& |y_i - H(x_i)|\leq\alpha & \\ \alpha(|y_i - H(x_i)|-\frac{\alpha}{2}) &|y_i - H(x_i)|>\alpha & \alpha \in (0, 1) \end{matrix}\right.$
quantile： $L = \sum{l(y_i,H(x_i))}$

$l =\left\{\begin{matrix} \alpha (y_i - H(x_i)),& y_i - H(x_i) > 0 & \\ 0, & y_i - H(x_i) = 0 & \alpha \in (0, 1)\\ (1-\alpha) (y_i - H(x_i)),& y_i - H(x_i) < 0 & \end{matrix}\right.$

(8)alpha (选取huber为损失函数时的阈值/选取quantile为损失函数时用以辅助计算输出结果，默认0.9）

损失函数的选择：

GBDT是工业应用最广泛的模型，工业数据大部分都极度偏态、具有长尾，因此GBDT必须考虑离群值带来的影响。Boosting是天生更容易被离群值影响的模型、也更擅长学习离群值的模型。

当高度关注离群值、并且希望将离群值预测正确时，选择平方误差。

工业中大部分的情况在实际进行预测时，离群值往往比较难以预测，因此离群样本的预测值和真实值之间的差异一般会较大。MSE作为预测值和真实值差值的平方，会放大离群值的影响，会让算法更加向学习离群值的方向进化，这可以帮助算法更好地预测离群值。

除离群值的影响、更关注非离群值的时候，选择绝对误差

MAE对一切样本都一视同仁，对所有的差异都只求绝对值，因此会保留样本差异最原始的状态。

试图平衡离群值与非离群值、没有偏好时，选择Huber或者Quantileloss。

Huberloss损失结合了MSE与MAE，在Huber的公式中，当预测值与真实值的差异大于阈值时，则取绝对值，小于阈值时，则取平方。HuberLoss是位于MSE和MAE之间的、对离群值相对不敏感的损失。

（9）属性loss_（返回具体的损失函数对象，而不会返回公式）

4、弱评估器结构相关的参数及属性

限制树模型生长结构的三个参数：

（10）max_depth：弱评估器被允许的最大深度

默认3；一般是树的最大生长深度（不含根），即总的迭代次数（迭代一次长一层）

对GBDT来说，无论是分类器还是回归器，默认的弱评估器最大深度都为3，因此GBDT默认就对弱评估器有强力的剪枝机制。

（11）min_samples_split：弱评估器分枝时，父节点上最少要拥有的样本个数

（12）min_samples_leaf：弱评估器的叶子节点上最少要拥有的样本个数

（14）min_weight_fraction_leaf：叶子节点所需最小权重和

当样本权重被调整时，叶子节点上最少要拥有的样本权重

（15）max_leaf_nodes：弱评估器上最多可以有的叶子节点数量

（16）min_impurity_decrease：弱评估器分枝时允许的最小不纯度下降量

（17）criterion：弱评估器分枝时的不纯度衡量指标

在sklearn当中，GBDT中的弱学习器 $f$ 是CART树，因此每棵树在建立时都依赖于CART树分枝的规则进行建立。CART树每次在分枝时都只会分为两个叶子节点（二叉树），它们被称为左节点(left)和右节点(right)。

不纯度下降量(impurity decrease)：父节点的不纯度与左右节点不纯度之和之间的差值。

GBDT中不纯度的衡量指标有2个：弗里德曼均方误差friedman_mse与平方误差squared_error。

弗里德曼均方误差friedman_mse

弗里德曼均方误差是由Friedman在论文《贪婪函数估计：一种梯度提升机器》（Greedy Function Approximation: A Gradient Boosting Machine）中提出的全新的误差计算方式。链接如下，pdf版本论文请点击文末链接下载。https://www.jstor.org/stable/2699986

基于弗里德曼均方误差的不纯度下降量：（大部分时候，也是默认使用的！！！不要轻易改动）

【左右叶子节点上样本量的调和平均 * (左叶子节点上均方误差 - 右叶子节点上的均方误差)^2】

$\frac{w_lw_r}{w_l \space + \space w_r} * \left( \frac{\sum_l{(r_i - \hat{y_i})^2}}{w_l} - \frac{\sum_r{(r_i - \hat{y_i})^2}}{w_r}\right)^2$

其中 $w$ 是左右叶子节点上的样本量，当我们对样本有权重调整时， $w$ 则是叶子节点上的样本权重。 $r_i$ 是样本i上的残差（父节点中样本i的预测结果与样本i的真实标签之差），也可能是其他衡量预测与真实标签差异的指标， $\hat{y_i}$ 是样本i在当前子节点下的预测值。

论文中：

弗里德曼均方误差使用调和平均数（分子上相乘分母上相加）来控制左右叶子节点上的样本数量，相比普通地求均值，调和平均必须在左右叶子节点上的样本量/样本权重相差不大的情况下才能取得较大的值。

在决策树进行分枝时，会偏向于建立一个不纯度非常非常低的子集，然后将剩下无法归入这个低不纯度子集的样本全部打包成另外一个子集。直接使用两个子集之间的MSE差距来衡量不纯度的下降量。

基于平方误差的不纯度下降量：

$\frac{\sum_p{(r_i - \hat{y_i})^2}}{w_l + w_r} - (\frac{w_l}{w_l+w_r} * \sum_l{(r_i - \hat{y_i})^2} + \frac{w_r}{w_l+w_r} * \sum_r{(r_i - \hat{y_i})^2})$

5、与提前停止问题相关的参数

一般情况下，无论使用什么算法，只要我们能够找到损失函数上真正的最小值，那模型就达到“收敛”状态，迭代就应该被停止。

在机器学习训练流程中，往往是通过给出一个极限资源来控制算法的停止，比如，我们通过超参数设置允许某个算法迭代的最大次数，或者允许建立的弱评估器的个数。

对于复杂度较高、数据量较大的Boosting集成算法来说，无效的迭代常常发生。比如在20次迭代时已经很接近最小值，为了完成我们最初设定的100次迭代，模型又进行了80次迭代，而这80次迭代带来的效果并不明显（只比20次迭代的结果小了一点点点点）。

我们根据以下原则来帮助梯度提升树实现提前停止：

在GBDT迭代过程中，只要损失函数的值持续减小、或验证集上的分数持续上升，我们就可以认为GBDT的效果还有提升空间。

GBDT已经达到了足够好的效果（非常接近收敛状态），持续迭代下去不会有助于提升算法表现

当测试集上的损失不再下降、持续保持平稳时，继续训练会浪费训练资源，迭代下去模型也会停滞不前，因此需要停止。如上图，我们应该在1000次迭代左右就停止迭代。

GBDT还没有达到足够好的效果（没有接近收敛），但迭代过程中呈现出越迭代算法表现越糟糕的情况

当测试集上的损失开始升高时，往往训练集上的损失还是在稳步下降，继续迭代下去就会造成训练集损失比测试集损失小很多的情况，也就是过拟合。如上图在迭代2500次左右就需要停止，如果继续迭代下去就会出现严重的过拟合的情况。

虽然GBDT还没有达到足够好的效果，但是训练时间太长/速度太慢，我们需要重新调整训练

可以通过参数verbose打印结果来观察，如果GBDT的训练时间超过半个小时，建树平均时长超出1分钟，我们就可以打断训练考虑重调参数。

（18）validation_fraction（验证集占比）

在实际数据训练时，我们需要从训练集中划分出一小部分数据，专用于验证是否应该提前停止。

从训练集中提取出、用于提前停止的验证数据占比，值域为[0,1]。

（19）n_iter_no_change（多少次下降无效则停止迭代）

验证集上的损失函数值连续n_iter_no_change次没有下降或下降量不达阈值时，则触发提前停止。默认设置为None，表示不进行提前停止。

（20）tol（损失函数下降的阈值）

默认值为1e-4，根据不同的损失函数设置不同的阈值。

当连续`n_iter_no_change`次迭代中，验证集上损失函数的减小值都低于阈值`tol`，或者验证集的分数提升值都低于阈值`tol`的时候，就令迭代停止

提前停止问题的实验：

#提前停止问题相关实验
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size=0.2,random_state=1409)

start = time.time()
reg_prestop = GBR(n_estimators=1000
          ,validation_fraction=0.2,n_iter_no_change=10,tol=0.001
          ,random_state=1409).fit(Xtrain,Ytrain)
print('提前停止：')
print(time.time()-start)
print(reg_prestop.n_estimators_)
print(reg_prestop.score(Xtest,Ytest))

start = time.time()
reg_norm = GBR(n_estimators=1000,random_state=1409).fit(Xtrain,Ytrain)
print('常规情况：')
print(time.time()-start)
print(reg_norm.n_estimators_)
print(reg_norm.score(Xtest,Ytest))

对比发现用少于十分之一的迭代时间和次数，迭代到了一个较好的测试集得分结果，后续900多次的迭代，只优化了不到0.007的得分。

用早停法的经验总结：

数据量非常大，迭代速度十分缓慢，用早停法节约运算时间。
n_estimators参数范围极广（需要500~1000棵树时），使用早停法来寻找可能的更小的n_estimators取值
当数据量非常小，模型很可能快速陷入过拟合状况时，开启提前停止来防止过拟合

6、和随机提升树相关的参数

随机森林中的袋外数据：随机森林在构建每棵树时，会对训练集使用不同的bootstrap sample（随机且有放回地抽取）。对于每棵树而言（假设对于第k棵树），大约有40%的训练实例没有参与第k棵树的生成，这40%的数据就称为第k棵树的袋外数据样本。

这40%的袋外数据可以用于对随机森林的结果进行验证。

在梯度提升树的原理当中，当每次建树之前进行随机抽样时，这种梯度提升树叫做随机提升树（Stochastic Gradient Boosting）。

（21）subsample (对数据的随机有放回抽样比例)

该参数被设置为1时，则不进行抽样，直接使用全部数据集进行训练。该参数不可设置为0.

（22）max_features（对特征的有放回抽样比例由参数）

（23）random_state（随机数种子）

在GBDT中进行又放回的随机抽样，也会产生和随机森林一样的袋外数据，也可以用于对每一个若评估器的结果进行验证。模型会保留这个过程的验证结果（上升或下降的结果）。

（24）属性oob_improvement_ （袋外分数的变化值）

（25）属性 train_score_（袋内分数的变化值）

7、其它注意点

klearn中的GBDT分类器并没有提供调节样本不均衡问题的参数class_weights；如果样本存在严重不均衡的状况，那我们可能会考虑不使用梯度提升树，或者先对数据进行样本均衡的预处理后，再使用梯度提升树。

GBDT中的树必须一棵棵建立、且后面建立的树还必须依赖于之前建树的结果，因此GBDT很难在某种程度上实现并行。

四、GBDT的参数空间和超参数优化

1、参数空间

learning_rate（整体学习速率）：单一弱评估器对整体算法的贡献。
init（初始化H0）：如果在其中填入具体的算法，过拟合可能会变得更加严重。
max_depth（粗剪枝）：GBDT中的默认值是3，无法通过降低来大规模降低模型复杂度，更难以用来控制过拟合，在GBDT当中，`max_depth`的调参方向是放大/加深，以探究模型是否需要更高的单一评估器复杂度。相对的在随机森林当中，`max_depth`的调参方向是缩小/剪枝，用以缓解过拟合。

最好的控制过拟合的方法就是增加随机性/多样性：

max_features（随机性）：对特征进行抽样。
subsamples（随机性）：对样本进行抽样。

选定参数空间，调参范围：

2、基于TPE对GBDT进行优化

（1）导包读数据

（2）建立benchmark

GBDT未进行参数优化前：5折验证运行时间0.49s；最优分数(RMSE)28793.994

可多验证几个基本算法：随机森林，TPE后的随机森林、AdaBoost等

（3）定义参数`init`需要的算法

之前实验init为调参后的随机森林效果最好。

（4）定义目标函数

#目标函数
def hyperopt_objective(params):
    reg = GBR(n_estimators = int(params["n_estimators"])
              ,learning_rate = params["lr"]
              ,criterion = params["criterion"]
              ,loss = params["loss"]
              ,max_depth = int(params["max_depth"])
              ,max_features = params["max_features"]
              ,subsample = params["subsample"]
              ,min_impurity_decrease = params["min_impurity_decrease"]
              ,init = rf
              ,random_state = 1409
              ,verbose = False)
    cv = KFold(n_splits=5, shuffle=True, random_state=1409)
    validation_loss = cross_validate(reg,X,y
                                     ,scoring="neg_root_mean_squared_error"
                                     , cv=cv
                                     , verbose=False
                                     , n_jobs=-1
                                     , error_score='raise')  
    return np.mean(abs(validation_loss["test_score"]))  #RMSE

（5）定义参数空间

param_grid_simple = {'n_estimators':hp.quniform("n_estimators",25,200,25)
                    ,"lr": hp.quniform("learning_rate",0.05,2.05,0.05)
                    ,"max_features": hp.choice("max_features",["log2","sqrt",16,32,64,"auto"])
                    ,"subsample": hp.quniform("subsample",0.1,0.9,0.1)
                    ,"loss":hp.choice("loss",["squared_error","absolute_error", "huber", "quantile"])
                    , "criterion": hp.choice("criterion", ["friedman_mse", "squared_error", "mse", "mae"])
                    ,"max_depth": hp.quniform("max_depth",2,30,2)
                    ,"min_impurity_decrease":hp.quniform("min_impurity_decrease",0,5,1)
                     }

这个参数空间的大小为：13171200（超大参数空间）

（6）优化函数

#优化函数
def param_hyperopt(max_evals=100):
    trials = Trials()       #保存迭代过程
    early_stop_fn = no_progress_loss(100)   #设置提前停止
    #定义代理模型
    params_beat = fmin(hyperopt_objective
                       ,space = param_grid_simple   #参数空间
                       ,algo = tpe.suggest  #最优化代理模型
                       ,max_evals = max_evals   #最大迭代次数
                       ,verbose = True  #打印迭代过程
                       ,trials = trials #保存迭代过程
                       , early_stop_fn = early_stop_fn    #设置提前停止
                        )
    print("\n", "\n", "best params: ", params_best,     #打印最优参数
          "\n")
    return params_best, trials

（7）验证函数

（可选）文末链接取py源码。本次实验暂不使用。

（8）初试训练贝叶斯优化器

刚开始用小的迭代次数30先试一试。

#训练贝叶斯
params_best, trials = param_hyperopt(30)

（9）调整参数空间及对应的目标函数

根据搜索结果修改空间范围、增加空间密度，一般以被选中的值为中心向两边拓展，并减小步长，同时范围可以向我们认为会被选中的一边倾斜。

根据上述三次实验的结果，发现：

loss参数的最优选择都是0号的“squared_error”，可以将本参数设为固定值，缩小参数空间。

criterion参数的最优选择都是“friedman_mse”，同样设为固定值，缩小参数空间。

max_depth被选为22，30，我们则将原本的范围(2,30,2)修改为(15,35,1)。

max_features被选为5和4，将原本的范围["log2","sqrt",16,32,64,"auto"]修改为（30，70，2）

……

#调整后的参数空间
param_grid_simple = {'n_estimators': hp.quniform("n_estimators",50,200,10)
                     ,"lr": hp.quniform("learning_rate",0.05,3,0.05)
                     ,"max_depth": hp.quniform("max_depth",15,35,1)
                     ,"subsample": hp.quniform("subsample",0.3,1,0.05)
                     ,"max_features": hp.quniform("max_features",30,70,2)
                     ,"min_impurity_decrease":hp.quniform("min_impurity_decrease",0,5,0.5)
                    }

根据上述结果继续修改空间范围、增加空间密度。也可增加迭代次数。

我们设定的是100次迭代无明显效果就停止，这个数值告诉我们迭代到107次就达到了我们理想数值。

（10）选定参数

选定参数后用（7）的验证函数进行的验证

#选定一组参数
start = time.time()
last_result = hyperopt_validation({'criterion': "friedman_mse",
                     'learning_rate': 0.8,
                     'loss': "squared_error",
                     'max_depth': 29.0,
                     'max_features': 64,
                     'min_impurity_decrease': 3.5,
                     'n_estimators': 190.0,
                     'subsample': 0.925})
print(last_result)
end = (time.time() - start)
print(end)

（11)分析总结

目前我们通过对GBDT的调参获得了目前最好的结果，RMSE为25243.304454969.。

这一组参数时间消耗较高，这个过程中构造了190棵树，在无法并行的情况下，逐棵构造用时消耗较大。但相比于未调参前的28792已经有了很大的提高。它具有较好的学习能力。

如果你看到了最后，想自己执行一遍代码。

所有评论(0)

查看更多评论

Wing以一

@qq_49183286

已为社区贡献2条内容

GBDT 梯度提升树（Gradient Boosting Decision Tree）长篇全解

Wing以一

一、相关基础知识

二、调用sklearn实现GBDT

1、梯度提升回归树

​

2、梯度提升分类树

三、参数&属性详解

1、迭代过程涉及的参数

（1）n_estimators（迭代次数）

（2）learning_rate（学习率参数）

(3) init (输入计算初始预测结果的估计器对象)

（4）属性init_ (模型被拟合完毕之后，返回输出的评估器对象)

2、分类任务涉及的参数

(5) 属性n_estimators_ （实际迭代次数）

(6) 属性estimators_ （实际建立的弱评估器数量）

3、损失函数涉及的参数

（7）loss （损失函数）

(8)alpha (选取huber为损失函数时的阈值/选取quantile为损失函数时用以辅助计算输出结果，默认0.9）

损失函数的选择：

（9）属性loss_（返回具体的损失函数对象，而不会返回公式）

4、弱评估器结构相关的参数及属性

（10）max_depth：弱评估器被允许的最大深度

（11）min_samples_split：弱评估器分枝时，父节点上最少要拥有的样本个数

（12）min_samples_leaf：弱评估器的叶子节点上最少要拥有的样本个数

（14）min_weight_fraction_leaf：叶子节点所需最小权重和

（15）max_leaf_nodes：弱评估器上最多可以有的叶子节点数量

（16）min_impurity_decrease：弱评估器分枝时允许的最小不纯度下降量

（17）criterion：弱评估器分枝时的不纯度衡量指标

5、与提前停止问题相关的参数

（18）validation_fraction（验证集占比）

（19）n_iter_no_change（多少次下降无效则停止迭代）

（20）tol（损失函数下降的阈值）

6、和随机提升树相关的参数

（21）subsample (对数据的随机有放回抽样比例)

（22）max_features（对特征的有放回抽样比例由参数）

（23）random_state（随机数种子）

（24）属性oob_improvement_ （袋外分数的变化值）

（25）属性 train_score_（袋内分数的变化值）

7、其它注意点

四、GBDT的参数空间和超参数优化

1、参数空间

2、基于TPE对GBDT进行优化

（1）导包读数据

（2）建立benchmark

（3）定义参数`init`需要的算法

（4）定义目标函数

（5）定义参数空间

（6）优化函数

（7）验证函数

（8）初试训练贝叶斯优化器

（9）调整参数空间及对应的目标函数

（10）选定参数

（11)分析总结

所有评论(0)

Wing以一

(3) init (输入计算初始预测结果 $H_0$ 的估计器对象)

（4）属性init_ (模型被拟合完毕之后，返回输出 $H_0$ 的评估器对象)