PID控制器算法-Simulink仿真
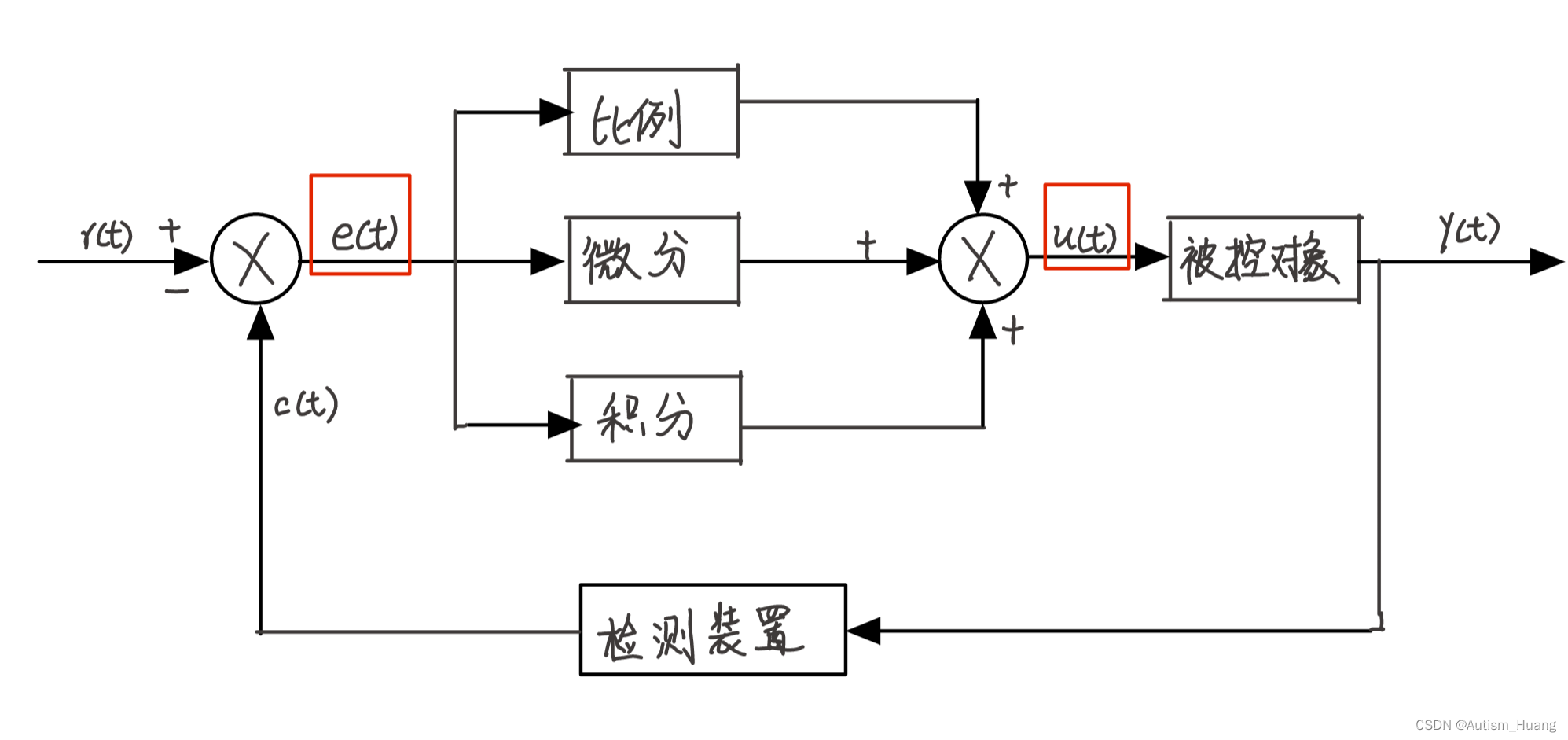
上图是一个闭环控制系统地框图:假设是调试一个电机的速度,上图的r(t)是目标速度,y(t)是速度输出量,e(t)是速度误差,u(t)是PID计算后发送给电机的输出值,被控对象是电机,假设PID控制器为C(s)=U(s)E(s)C(s)=\frac{U(s)}{E(s)}C(s)=E(s)U(s),传递函数为G(s)=Y(s)U(s)G(s)=\frac{Y(s)}{U(s)}G(s)=U(s)Y
PID控制算法
概述

上图是一个闭环控制系统地框图:
假设是调试一个电机的速度,上图的r(t)是目标速度,y(t)是速度输出量,e(t)是速度误差,u(t)是PID计算后发送给电机的输出值,被控对象是电机,假设PID控制器为 C ( s ) = U ( s ) E ( s ) C(s)=\frac{U(s)}{E(s)} C(s)=E(s)U(s),传递函数为 G ( s ) = Y ( s ) U ( s ) G(s)=\frac{Y(s)}{U(s)} G(s)=U(s)Y(s),检测装置为H(s),也就是反馈函数。
那么该系统闭环传递函数就为 ϕ ( s ) = Y ( s ) R ( s ) = C ( s ) G ( s ) 1 + C ( s ) G ( s ) H ( s ) \phi(s)=\frac{Y(s)}{R(s)}=\frac{C(s)G(s)}{1+C(s)G(s)H(s)} ϕ(s)=R(s)Y(s)=1+C(s)G(s)H(s)C(s)G(s)。
PID传递函数形式:
G
(
s
)
=
U
(
s
)
E
(
s
)
=
K
s
[
1
+
1
T
i
s
+
T
d
s
]
G(s)=\frac{U(s)}{E(s)}=K_s[1+\frac{1}{T_is}+T_ds]
G(s)=E(s)U(s)=Ks[1+Tis1+Tds]

PID的微分方程形式:
u
(
t
)
=
K
c
[
e
(
t
)
+
1
T
i
∫
0
t
e
(
t
)
d
t
+
T
d
d
e
(
t
)
d
t
]
+
u
0
u(t)=K_c[e(t)+\frac{1}{T_i}\int_0^te(t)dt+T_d\frac{de(t)}{dt}]+u_0
u(t)=Kc[e(t)+Ti1∫0te(t)dt+Tddtde(t)]+u0
式中: K c 、 T i 、 T d K_c、T_i、T_d Kc、Ti、Td分别为模拟调节器的比例增益、积分时间和微分时间,u0为偏差e=0时的调节器输出,又称之为稳态工作点。
也可以写成 u ( t ) = [ K p e ( t ) + K i ∫ 0 t e ( t ) d t + K d d e ( t ) d t ] + u 0 u(t)=[K_pe(t)+K_i\int_0^te(t)dt+K_d\frac{de(t)}{dt}]+u_0 u(t)=[Kpe(t)+Ki∫0te(t)dt+Kddtde(t)]+u0
其中:
比例系数
K
p
=
K
c
K_p=K_c
Kp=Kc
积分系数 K i = K c T i K_i=\frac{K_c}{T_i} Ki=TiKc
微分系数 K d = K c T d K_d=\frac{K_c}{T_d} Kd=TdKc
误差e(t)
对于我们为什么需要PID
对于为什么需要做闭环控制,因为我们在实际应用中可能需要要求量纲在一定时间内保持恒定,因此一个系统就必须不断地接收输出的反馈进而控制输入的大小。以控制一个温度为例,一个加热棒需要保持在30摄氏度,但是由于天气的原因,可能没有办法自然加热到30摄氏度,因此在一个温控系统接收到温度达不到目标温度时,就会加大自身的功率来加热,使得加热棒达到目标温度。反之,如果加热过高了,系统接收到反馈量就会自主地降低自身的输入,从而保持温度的恒定。

所以我们一般会将受控对象的反馈(measured output)与我们期望的reference输入相减,那么我们就可以得到一个error误差值,得到这个误差值之后,我们可以将该误差作为输入量给PID控制器Controller,控制器最后输出结果control input直接传给受控对象Plant
浅析 K p K_p Kp的作用(有差调节)
比例项: K p × e r r ( t ) K_p×err(t) Kp×err(t)
-
对偏差量e(t)瞬间作出反应,只与当前的偏差有关,产生相应的控制量u(t)。
-
控制作用的强弱取决于比例系数 K p K_p Kp
也就是说 K p K_p Kp越大,作用越强,过程越快,静态偏差也就越小。
-
但是 K p K_p Kp越大,也越容易产生振荡,增加系统的超调量,系统的稳定性会变差。
总结:如果一味地增大比例项,静差虽然会减小,但是超调也增大了很多。所以我们可以看出纯比例控制所遇到的一个矛盾的问题,系数太小则存在静差,系数太大则存在超调,所以为了解决这一问题,我们需要提高系统阶数,引入积分项。

当 K i 、 K d K_i、K_d Ki、Kd都为0时, K p K_p Kp的大小影响着输出曲线的形状。
浅析 K i K_i Ki的作用
其实 K i = K c T i K_i=\frac{K_c}{T_i} Ki=TiKc,积分项: K i × ∫ e r r ( t ) d t K_i×\int err(t)dt Ki×∫err(t)dt
- 只要偏差e(t)存在,积分作用就会不断地增加(前提条件是控制器没有饱和),偏差e(t)就不断减小,当偏差e(t)=0时,积分控制作用才会停止。
- 积分控制会降低系统的响应速度。
- 积分作用太强会增加系统的超调量,系统的稳定性会变差。
总结:积分项虽然可以消除静差,但是在一定程度上会助长超调的影响,使得系统趋于稳定的时间变得更久。

当 K p = 1 、 K d = 0 K_p=1、K_d=0 Kp=1、Kd=0时, K i K_i Ki的大小影响着输出曲线的形状。
浅析 K d K_d Kd的作用
其实 K d = K c T i K_d={K_c}{T_i} Kd=KcTi,微分项: K d × d e r r ( t ) d t K_d×\frac{derr(t)}{dt} Kd×dtderr(t)
微分就是求导,求导体现的就是斜率、变化率,是一种趋势,微分越大,就证明微分的作用越强。
- 微分环节可以根据偏差e(t)的变化趋势(变化速度)预先给出纠正作用,能在偏差变大之前进行修正。
- 有助于减小超调量,克服震荡,使系统趋于稳定,它加快了系统的跟踪速度,减少调节时间。
- 但微分作用对输入信号的噪声很敏感,对那些噪声较大的系统一般不用微分,或在微分之前对输入信号进行滤波。
总结:每当_err(t)_产生急剧变化时,就会产生一个很大的微分项来抵消这一急剧的变化。这就恰好和我们的超调现象相对应,因为超调正是一个急剧上升后急剧下降的尖峰,而微分项是来和它做抵消的。

当 K p = 1 、 K i = 1 K_p=1、K_i=1 Kp=1、Ki=1时, K d K_d Kd的大小影响着输出曲线的形状。(Kd=1的效果好)
将连续函数转化为离散函数
关于前面讲到的其实是时域上的操作,单片机内部是一个数字系统,数字系统必然是离散的,所以我们要把连续型PID转化为离散型PID,积分转为离散其实就是求和,微分转为离散就是差分而已,即:
U
(
n
)
=
K
p
∗
e
r
r
(
n
)
+
K
p
T
T
i
∗
∑
e
r
r
(
n
)
+
K
p
T
d
T
∗
[
e
r
r
(
n
)
−
e
r
r
(
n
−
1
)
]
U(n)=K_p*err(n)+\frac{K_pT}{T_i}*\sum err(n)+\frac{K_pT_d}{T}*[err(n)-err(n-1)]
U(n)=Kp∗err(n)+TiKpT∗∑err(n)+TKpTd∗[err(n)−err(n−1)]
但是由于T是一个周期常数,所以公式也可以转化为:
U
(
n
)
=
K
p
∗
e
r
r
(
n
)
+
K
i
∗
∑
e
r
r
(
n
)
+
K
d
∗
[
e
r
r
(
n
)
−
e
r
r
(
n
−
1
)
]
U(n)=K_p*err(n)+K_i*\sum err(n)+K_d*[err(n)-err(n-1)]
U(n)=Kp∗err(n)+Ki∗∑err(n)+Kd∗[err(n)−err(n−1)]
要求:
-
PID运算必须要在周期任务内(可以理解为定时器中断)完成。
-
采样周期和控制周期会影响到系数。
一般来说增加控制周期和采样周期是可以让我们的控制变得更加平滑,控制周期即执行控制代码的周期,一般是放置运算PID代码的定时器的周期,采样周期即获取传感器数据的周期,比如电机的采样周期就是CAN接收中断的周期。
结合官方开源代码
这是pid.c下的pid_calculate函数,结合公式可以很容易理解含义。set即期望,get即反馈,两者相减得到误差err,pid→pout即比例项,直接将err线性放大,pid→iout即积分项,对err进行累加,pid→dout即微分项,对err做差分。最后将三者叠加得到pid控制器输出。
/**
* @brief calculate delta PID and position PID
* @param[in] pid: control pid struct
* @param[in] get: measure feedback value
* @param[in] set: target value
* @retval pid calculate output
*/
float pid_calculate(struct pid *pid, float get, float set)
{
pid->get = get;
pid->set = set;
pid->err = set - get;
if ((pid->param.input_max_err != 0) && (fabs(pid->err) > pid->param.input_max_err))
return 0;
pid->pout = pid->param.p * pid->err;
pid->iout += pid->param.i * pid->err;
pid->dout = pid->param.d * (pid->err - pid->last_err);
abs_limit(&(pid->iout), pid->param.inte_limit);
pid->out = pid->pout + pid->iout + pid->dout;
abs_limit(&(pid->out), pid->param.max_out);
return pid->out;
}
Simulator仿真图

关于系统辨识以及根据系统辨识的结果设计控制器,可以参考官方的开源教程:
https://bbs.robomaster.com/thread-4941-1-1.html
https://bbs.robomaster.com/thread-5059-1-1.html
从本质上理解PID控制:

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容





所有评论(0)