大纲

一、背景

二、入门

三、进阶

四、放弃

五、验证

背景

dp即dynamic programming，动态规划的英文缩写。

本质上，它是一种多阶段决策的最优解模型，一般用来求最值问题。

多阶段决策（重叠子问题），意味着过程可拆解，每个阶段的子问题重复叠加变成最终问题。

最优解模型（最优子结构），由每个子问题的最优，进而递推到全局最优。

最值问题，比如满足xx情况下使用的最小代价，最大收益等等。

什么情况下考虑用dp解决，或者说什么场景下满足dp：

1、可以拆解成重叠子问题，且能找到最优子结构。

2、无后向性：当前阶段的最优解，只关注前面的数据和产出，不会受到后续内容的影响。

确定了是dp问题之后的核心目标：确定状态转移方程

状态转移方程是求解的关键步骤。

简单版：本阶段的状态是上一个阶段的状态和上一个阶段决策的结果转移的方式。

复杂版：本阶段的状态是前面阶段的状态和前面阶段决策，基于一定的条件筛选，得到的结果转移方式。

转移方程体现形式：dp[i] = func(dp[0], dp[1], dp[2], ... dp[i-1])

比如：dp[i] = dp[i-2] + dp[i-1]

所以dp问题主要分两步：

1、确定是dp问题。

2、确定状态转移方程。

入门

目标：感受dp的过程，理解状态转移方程是怎么回事。

核心思想：dp解题思想的建立。

题目：

1、斐波那契数列

给定数列：1，1，2，3，5。。。

求第n项。

2、跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。

求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

正常解题 -> dp思想转变

1、斐波那契数列

给定数列：1，1，2，3，5。。。

求第n项。

正常解题

递归即可搞定，递归复杂度过高，则利用变量，循环即可搞定。

public int Fibonacci(int n) {
    if (n <= 2) {
        return 1;
    }
    int first = 1;
    int second = 1;
    for (int idx = 3; idx <= n; idx ++) {
        int cur = first + second;
        first = second;
        second = cur;
    }
    return second;
}

dp思想

一、确定是不是dp？

1、当前每步都是和前面几步有关系，当前第n步是第n-1和第n-2步影响的。

2、每步的结果只受前面步子的影响。

结论成立，dp。

二、确定状态转移方程

本质上就是确定dp[i]怎么来。

很明显，斐波那契数列给了公式：

if i == 1 or i == 2:
	dp[i] = 1
else:
	dp[i] = dp[i-1] + dp[i-2]

产出代码：

public int Fibonacci(int n) {
    if (n <= 2) {
        return 1;
    }
    int[] dp = new int[n];
    dp[0] = dp[1] = 1;
    for (int idx = 2; idx < n; idx ++) {
        dp[idx] = dp[idx-1] + dp[idx-2];
    }
    return dp[n-1];
}

可以看到，当前的dp，每个位置存的值都是当前位置对应的结果。

回顾一下做法：

1、找到当前dp[i]的赋值方式，使用的内容主要考虑为dp[0],dp[1],...dp[n-1]，

这里主要使用dp[i-1]和dp[i-2]

2、当前dp满足最小自动推动的有两项，即dp[0] 和 dp[1]，所以前两项需要手动赋值。

2、跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。

求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

正常解题

看不看得出来，先列几项答案总没错。

第一级台阶，智能跳1级。共一种跳法。
第二级台阶，可以是一次跳2级，可以是连续两次1级。共两种跳法。
        	穷举一下，可以是[1,1] 和 [2],共两种。
第三级台阶，可以是从第一级台阶直接跳两级，也可以是第二级台阶直接跳一级。
					穷举一下，可以是[1,1,1],[1,2],[2,1],共三种。
第四级台阶。。。
。。。规律出来了。。。
第n级台阶，可以是第n-1级台阶直接跳一级，也可以是第n-2级台阶直接跳两级。
          即将n-1级跳法的种数 + n-2级跳法的种数 得到结果。

同斐波那契数列数列基本大差不差，就差了初始项。

public int jumpFloor(int target) {
    if (target <= 3) {
        return target;
    }
    int first = 1;
    int second = 2;
    for (int idx = 3; idx <= target; idx ++) {
        int temp = first + second;
        first = second;
        second = temp;
    }
    return second;
}

dp思想

一、确定是不是dp？

1、当前每步都是和前面几步有关系，当前第n步是第n-1和第n-2步影响的。

2、每步的结果只受前面步子的影响。

结论成立，dp。

二、确定状态转移方程

本质上就是确定dp[i]怎么来。

很明显：

if i == 1 or i == 2:
	dp[i] = i
else:
	dp[i] = dp[i-1] + dp[i-2]

产出代码：

public int jumpFloor2(int target) {
    if (target <= 3) {
        return target;
    }

    int[] dp = new int[target];
    dp[0] = 1;
    dp[1] = 2;
    for (int idx = 2; idx < target; idx ++) {
        dp[idx] = dp[idx-1] + dp[idx-2];
    }
    return dp[target-1];
}

回顾一下做法：

1、找到当前dp[i]的赋值方式，使用的内容主要考虑为dp[0],dp[1],...dp[n-1]，

这里仍然是使用dp[i-1]和dp[i-2]

2、当前dp满足最小自动推动的也是两项，即dp[0] 和 dp[1]，所以前两项需要手动赋值。

到这里，可以说，dp是入门了，知道什么是dp，知道dp的效果是怎么回事。

但还做不了题。

进阶

目标：可以上手做一些简单的dp问题。

核心思想：递推公式摸索，最小辅助准备。

题目列表：

1、爬楼梯最小费用

给定一个整数数组cost，其中cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用，下标从0开始。

一旦你支付此费用，即可选择向上爬一个或者两个台阶。你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例：

输入：[2,5,20]

返回值：5

说明：你将从下标为1的台阶开始，支付5 ，向上爬两个台阶，到达楼梯顶部。总花费为5

2、严格上升子序列的长度

给定一个长度为 n 的数组 arr，求它的最长严格上升子序列的长度。

所谓子序列，指一个数组删掉一些数（也可以不删）之后，形成的新数组。例如 [1,5,3,7,3] 数组，其子序列有：[1,3,3]、[7] 等。但 [1,6]、[1,3,5] 则不是它的子序列。

我们定义一个序列是 严格上升 的，当且仅当该序列不存在两个下标 i 和 j 满足 i<j 且 arri ≥arrj。

示例：

输入：[6,3,1,5,2,3,7]

返回值：4

说明：该数组最长上升子序列为 [1,2,3,7] ，长度为4

3、最大连续子数组的和

输入一个长度为n的整型数组array，数组中的一个或连续多个整数组成一个子数组，子数组最小长度为1。求所有子数组的和的最大值。

示例：

输入：[1,-2,3,10,-4,7,2,-5]

返回值：18

说明：经分析可知，输入数组的子数组[3,10,-4,7,2]可以求得最大和为18

1、爬楼梯最小费用

给定一个整数数组cost，其中cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用，下标从0开始。

一旦你支付此费用，即可选择向上爬一个或者两个台阶。你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例：

输入：[2,5,20]

返回值：5

说明：你将从下标为1的台阶开始，支付5 ，向上爬两个台阶，到达楼梯顶部。总花费为5

补充说明：这里指的是要爬过最后一格为止，比如这里就是到达第4格。

一、分析题目，确认dp

支付当前格费用，就可以选择上爬一格或两格。

所以无论到多少格，都可以和前面的两格进行关联，

同时也只取决于前面两格历史积累及当前费用的最小挂钩，dp无疑。

二、状态转移方程

用一维数组，每个位置对应的数代表当前格子的开销。

dp[i] = min(dp[i-2] + cost[i-2]，dp[i-1] + cost[i-1])

这里的dp[i] 代表当前位置对应的最小开销。

看起来，最小自动前推需要有前两项。

上代码

public int minCostClimbingStairs (int[] cost) {
    if (cost.length <= 1) {
        return 0;
    }
    int[] result = new int[cost.length + 1];
    result[0] = 0;
    result[1] = 0;

    for (int idx = 2; idx <= cost.length; idx ++) {
        result[idx] = Math.min(result[idx-1] + cost[idx-1], result[idx-2] + cost[idx-2]);
    }
    return result[cost.length];
}

2、严格上升子序列的长度

给定一个长度为 n 的数组 arr，求它的最长严格上升子序列的长度。

所谓子序列，指一个数组删掉一些数（也可以不删）之后，形成的新数组。例如 [1,5,3,7,3] 数组，其子序列有：[1,3,3]、[7] 等。但 [1,6]、[1,3,5] 则不是它的子序列。

我们定义一个序列是 严格上升 的，当且仅当该序列不存在两个下标 i 和 j 满足 i<j 且 arri ≥arrj。

示例：

输入：[6,3,1,5,2,3,7]

返回值：4

说明：该数组最长上升子序列为 [1,2,3,7] ，长度为4

一、分析题目，确认dp

当前步子的最长依赖于前面步子的最长，且等于前面步子最后一个小于当前位置数值的长度+1。

满足重叠子问题 & 最优子结构 & 无后向性，dp问题无疑。

二、状态转移方程

当前位置可能会比前面若干个位置的值都大，找到最大的那个，进行加一，即为当前位置的目标值。

dp[0] = 1, dp[i] = max(dp[idx]) + 1, idx = [0,i-1] if num[i] > dp[idx], 如果都没有符合条件，dp[i] = 1

这里dp[i] 代表当前位置对应的最大上升序列长度。

看起来依赖项只需要一个，因此对第一项进行赋初值就ok。

上代码

public int LIS (int[] arr) {
    if (arr.length <= 1) {
        return arr.length;
    }

    int[] result = new int[arr.length];
    result[0] = 1;
    for (int idx = 1; idx < arr.length; idx ++) {
        int maxNum = 0;
        for (int idy = 0; idy < idx; idy ++) {
            if (arr[idx] > arr[idy]) {
                maxNum = Math.max(result[idy] + 1, maxNum);
            }
        }
        result[idx] = maxNum == 0 ? 1 : maxNum;
    }

    int maxNum = 0;
    for (int each : result) {
        maxNum = Math.max(each, maxNum);
    }
    return maxNum;
}

3、最大连续子数组的和

输入一个长度为n的整型数组array，数组中的一个或连续多个整数组成一个子数组，子数组最小长度为1。求所有子数组的和的最大值。

示例：

输入：[1,-2,3,10,-4,7,2,-5]

返回值：18

说明：经分析可知，输入数组的子数组[3,10,-4,7,2]可以求得最大和为18

一、分析题目，确认dp

当前步子的数是前面子数组的延伸，若子数组和在变大，则继续往后，且当前步子只受前面的影响。

满足重叠子问题 & 最优子结构 & 无后向性，dp问题无疑。

二、状态转移方程

dp[i] = max(dp[i-1] + array[i], array[i])

dp[i] 代表连续到当前位置，最大的值

上代码

public int FindGreatestSumOfSubArray(int[] array) {
    if (array.length == 1) {
        return array[0];
    }

    int[] result = new int[array.length];
    result[0] = array[0];
    int maxNum = result[0];
    for (int idx = 1; idx < array.length; idx++) {
        result[idx] = Math.max(array[idx], result[idx-1] + array[idx]);
        maxNum = Math.max(maxNum, result[idx]);
    }
    return maxNum;
}

放弃

目标：可以做一些比较难的dp问题。

题目列表

1、最长公共子序列

给定两个字符串str1和str2，输出两个字符串的最长公共子序列。如果最长公共子序列为空，则返回"-1"。目前给出的数据，仅仅会存在一个最长的公共子序列

示例：

输入："1A2C3D4B56","B1D23A456A"

返回值："123456"

2、最长公共子串

给定两个字符串str1和str2,输出两个字符串的最长公共子串

题目保证str1和str2的最长公共子串存在且唯一。

示例：

输入："1AB2345CD","12345EF"

返回值："2345"

3、编辑距离

给定两个字符串 str1 和 str2 ，请你算出将 str1 转为 str2 的最少操作数。

你可以对字符串进行3种操作：

1.插入一个字符

2.删除一个字符

3.修改一个字符。

示例：

输入："nowcoder","new"

返回值：6

说明："nowcoder"=>"newcoder"(将'o'替换为'e')，修改操作1次 "nowcoder"=>"new"(删除"coder")，删除操作5次

1、最长公共子序列

给定两个字符串str1和str2，输出两个字符串的最长公共子序列。如果最长公共子序列为空，则返回"-1"。目前给出的数据，仅仅会存在一个最长的公共子序列

示例：

输入："1A2C3D4B56","B1D23A456A"

返回值："123456"

一、分析题目，确认dp

用两个指针来看，一个指针对第一个串从前往后，第二个指针对第二个串从前往后。

当前位置的串是否一致，若一致，则长度与前面一个有关联。

若不一致，则延续两者最大的。

满足重叠子问题 & 最优子结构 & 无后向性，dp问题无疑。

二、状态转移方程

if str[i] == str[j]：
		then dp[i][j] = dp[i-1][j-1] + 1
else：
    dp[i][j] = max(dp[i-1][j],dp[i][j-1])

举个例子

 *   1 A 2 C 3 D 4 B 5 6
 * B 0 0 0 0 0 0 0 1 1 1
 * 1 1 1 1 1 1 1 1 1 1 1
 * D 1 1 1 1 1 2 2 2 2 2
 * 2 1 1 2 2 2 2 2 2 2 2
 * 3 1 1 2 2 3 3 3 3 3 3
 * A 1 2 2 2 3 3 3 3 3 3
 * 4 1 2 2 2 3 3 4 4 4 4
 * 5 1 2 2 2 3 3 4 4 5 5
 * 6 1 2 2 2 3 3 4 4 5 6
 * A 1 2 2 2 3 3 4 4 5 6

上代码

public String LCS (String s1, String s2) {
    if (null == s1 || null == s2 || s1.length()== 0 || s2.length()==0) {
        return "-1";
    }
    int row = s2.length();
    int column = s1.length();

    // 整型数组默认值都为0，此时第0行第0列还不需要额外赋初值了
    int[][] result = new int[row+1][column+1];
    for (int idxRow = 1; idxRow < row+1; idxRow++) {
        for (int idxColumn = 1; idxColumn < column+1; idxColumn++){
            if (s1.charAt(idxColumn-1) == s2.charAt(idxRow-1)) {
                result[idxRow][idxColumn] = result[idxRow-1][idxColumn-1] + 1;
            } else {
                result[idxRow][idxColumn] = Math.max(result[idxRow-1][idxColumn],result[idxRow][idxColumn-1]);
            }
        }
    }

    // 多造一列数据的好处在于回找时不用担心边界。。。
    StringBuilder strResult = new StringBuilder();
    int idxRow = row, idxColumn = column;
    while (idxRow >= 0 && idxColumn >= 0 && result[idxRow][idxColumn] > 0) {
        if (s1.charAt(idxColumn-1) == s2.charAt(idxRow-1)) {
            strResult.append(s1.charAt(idxColumn-1));
            idxRow--;
            idxColumn--;
        } else if (result[idxRow-1][idxColumn] > result[idxRow][idxColumn-1]) {
            idxRow--;
        } else {
            idxColumn--;
        }
    }

    return strResult.length() == 0 ? "-1" : strResult.reverse().toString();
}

2、最长公共子串

给定两个字符串str1和str2,输出两个字符串的最长公共子串

题目保证str1和str2的最长公共子串存在且唯一。

示例：

输入："1AB2345CD","12345EF"

返回值："2345"

一、分析题目，确认dp

用两个指针来看，一个指针对第一个串从前往后，第二个指针对第二个串从前往后。

当前位置的串是否一致，若一致，则长度与前面一个有关联。

若不一致，则当前位置可以置0，代表当前位置不同，每一步均相同的方式，且无关于后续。

满足重叠子问题 & 最优子结构 & 无后向性，dp问题无疑。

二、状态转移方程

如果当前两个位置的值不同，则认为当前两者位置到当前位置为止，其公共子序列为0。

若当前两个位置的值相同，则考虑是两串前一个位置的结果值 + 1。

dp[i][j] = dp[i-1][j-1] + 1 if str1[i] == str2[j] else dp[i][j] = 0

上代码

public String LCS (String str1, String str2) {
    if (null == str1 || null == str2 || str1.length() == 0 || str2.length() == 0) {
        return "";
    }
  	// 考虑第0行和第0列，均赋值为0，获取一个辅助数组
    int[][] result = new int [str2.length() + 1][str1.length() + 1];
    int maxLength = 0;
    int lastIndex = 0;
    for (int row = 1; row < str2.length() + 1; row ++) {
        for (int column = 1; column < str1.length() + 1; column ++) {
            if (str1.charAt(column - 1) == str2.charAt(row - 1)) {
                result[row][column] = result[row-1][column-1] + 1;
                if (result[row][column] > maxLength) {
                    maxLength = result[row][column];
                    lastIndex = column - 1;
                }
            } else {
                result[row][column] = 0;
            }
        }
    }
    // 这个需要注意最后的位置，两者都要加一，subString是左闭右开。
    return str1.substring(lastIndex - maxLength + 1, lastIndex + 1);
}

3、编辑距离

给定两个字符串 str1 和 str2 ，请你算出将 str1 转为 str2 的最少操作数。

你可以对字符串进行3种操作：

1.插入一个字符

2.删除一个字符

3.修改一个字符。

示例：

输入："nowcoder","new"

返回值：6

说明："nowcoder"=>"newcoder"(将'o'替换为'e')，修改操作1次 "nowcoder"=>"new"(删除"coder")，删除操作5次

一、分析题目，确认dp

类同上题，用两个指针来看，一个指针对第一个串从前往后，第二个指针对第二个串从前往后。

每个串的变动依赖于之前的吻合情况，在之前最小改动下满足两者一致即可。

满足重叠子问题 & 最优子结构 & 无后向性，dp问题无疑。

二、状态转移方程

两个串遍历过程中存在快慢，比如可以是快者删一个，可以是慢者加一个，也可以是修改一个。

本质上对应三个位置，即当前位置的上方、左边（看是谁快），和左上方（修改）。

dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1

上代码

public int editDistance(String str1, String str2) {
    if (null == str1 || str1.length() == 0) {
        return str2.length();
    }
    if (null == str2 || str2.length() == 0) {
        return str1.length();
    }

    int[][] dp = new int[str2.length()][str1.length()];
    dp[0][0] = str1.charAt(0) == str2.charAt(0) ? 0 : 1;
    for (int row = 1; row < str2.length(); row++) {
        dp[row][0] = dp[row - 1][0] + 1;
    }
    for (int column = 1; column < str1.length(); column++) {
        dp[0][column] = dp[0][column - 1] + 1;
    }

    for (int row = 1; row < str2.length(); row++) {
        for (int column = 1; column < str1.length(); column++) {
            if (str1.charAt(column) == str2.charAt(row)) {
                dp[row][column] = dp[row - 1][column - 1];
            } else {
                dp[row][column] = Math.min(dp[row - 1][column - 1], Math.min(dp[row - 1][column], dp[row][column - 1])) + 1;
            }
        }
    }

    return dp[str2.length() - 1][str1.length() - 1];
}

验证

目标：找几道不同难度的题验证验证整体水平

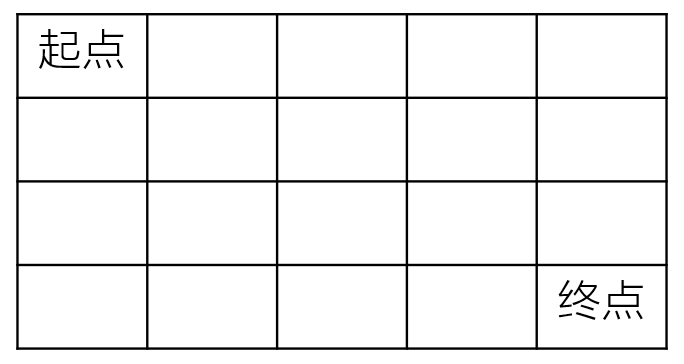
1、不同路径数I

一个机器人在m×n大小的地图的左上角（起点）。

机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。

可以有多少种不同的路径从起点走到终点？

备注：m和n小于等于100,并保证计算结果在int范围内

2、不同路径数II

给定一个m*n的地图，其中加入了一些障碍。每次只能向下或者向右走，问从左上角走到右下角有多少不同的路径？分别用0和1代表空区域和障碍。

备注：m和n不超过100.

示例：

[
    [0,0,0],
    [0,1,0],
    [0,0,0]
]

有2条不同的路径

3、打家劫舍I

你是一个经验丰富的小偷，准备偷沿街的一排房间，每个房间都存有一定的现金，为了防止被发现，你不能偷相邻的两家，即，如果偷了第一家，就不能再偷第二家；如果偷了第二家，那么就不能偷第一家和第三家。

给定一个整数数组nums，数组中的元素表示每个房间存有的现金数额，请你计算在不被发现的前提下最多的偷窃金额。

示例：

输入：[1,2,3,4]

返回值：6

说明：最优方案是偷第 2，4 个房间

4、打家劫舍II

你是一个经验丰富的小偷，准备偷沿湖的一排房间，每个房间都存有一定的现金，为了防止被发现，你不能偷相邻的两家，即，如果偷了第一家，就不能再偷第二家，如果偷了第二家，那么就不能偷第一家和第三家。沿湖的房间组成一个闭合的圆形，即第一个房间和最后一个房间视为相邻。

给定一个长度为n的整数数组nums，数组中的元素表示每个房间存有的现金数额，请你计算在不被发现的前提下最多的偷窃金额。

示例：

输入：[1,2,3,4]

返回值：6

说明：最优方案是偷第 2 4 个房间