概率论的学习整理4:全概率公式
全概率公式,联合概率之和,条件概率* 条件发生概率之和
·
1全概率的前置概念
弄清楚 全概率,全概率公式之前,需要先搞明白 条件概率和 联合概率的概念。
1.1 联合概率,joint probability
两个事件同时发生的概率
- 也可以称为 相交概率?
- P(AB)
- 两个事件同时发生的概率
- P(AB) = P(A ∩ B)
- P(A ∩ B) = P(B)P(A | B) = P(A)P(B | A)
1.2 条件概率, Conditional probability
在其他事件已经发生之后,此事件发生的概率。
- 条件概率
- P(B | A) =P(AB) / P(A)
- 条件概率等于,两者同时发生概率/ 先发生事件的概率
1.3 全概率
- 一般来说,没有这个概率吧
- 全概率=概率=1个完整的概率而已
- 这个概率一般是 [0,1] ,一般来说都是小于1的
1.4 有人说, 全概率 =1? NO!
- 全概率=1? NO
- 全概率只是某一个事件的全部概率,并不是全部概率空间!!!
- 所以全概率公式,只是用来计算某一个概率的公式,不存在全概率必须=1这么无厘头的问题
2 全概率公式
2.1 定义
- 百度的定义:
- 若事件A1,A2,…构成一个完备事件组且都有正概率,则对任意一个事件B,有如下公式成立:
- 就是联合概率之和
- P(B)=P(BA1)+P(BA2)+...+P(BAn)
- 也是条件概率*条件发生概率之和
- P(B) =P(B|A1)P(A1) + P(B|A2)P(A2) + ... + P(B|An)P(An)=P(BA1)+P(BA2)+...+P(BAn)
- 此公式即为全概率公式。
- 如果这个空间划分完备空间的事件,刚好是两个对立事件。
- P(B)=P(B|A)P(A)+P(B|A')P(A')
- 其中A A'是一个空间的完整划分
2.2 重点1: 全概率公式里,几个划分事件必须组成一个完备空间S,并且互斥不相交
全概率公式里
- 几个划分事件必须组成一个完备空间S的全划分(完整划分)
- 既然a1--an是一个空间的完整花费,这些概率之和为1
- 并且互斥不相交
2.2.1 为什么必须互斥不相交
- 见下图
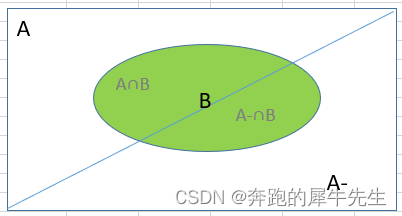
- 图1,A和A- 不相交
- 图2,A和A- 相交,相交部分是两个正方形的 红 & 黄 生成的橙色部分
- 如果空间划分的事件,A,A-,有重合/相交的部分,那么 P(A ∩B) 和 P(B ∩A') 就会有重合的部分,如图中椭圆里抠出来的竖条橙色的部分,会被计算2次,所以P(B) < P(AB) + P(BA') ,因此得到反证。


2.2.2 为什么必须是能组成完备的一个全划分呢(完整划分)?
- 很显然,如上图
- P(B)=P(AB) + P(BA')
- 显然,
- P(B) <>! P(AB)
- P(B) <>!P(BA')
2.3 全概率公式
某一个事件概率 = 这个事件*其他完备事件划分联合概率之和
- 对 P(B)=P(AB) + P(BA')
- 错 P(B)=P(A) + P(A')
某一个事件概率=条件概率*条件发生概率之和
- 对 P(B)=P(A) *P(B|A) + P(A')*P(B|A')
- 对 P(B)=P(A) *P(B|A) + P(A')*P(B|A') + P(A'')*P(B|A'')
下图是网图,可以借助理解


开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献64条内容
已为社区贡献64条内容





所有评论(0)