Marching Cubes 算法初探

浅浅学习一下 Marching Cubes 算法（较原始版本），这是将隐式表面提取为显示 mesh 的常见方法。主要基于前辈们的博客和笔记进行整理。

WoooChi

4817人浏览 · 2023-05-19 09:28:12

WoooChi · 2023-05-19 09:28:12 发布

Marching Cubes 学习笔记

一、背景
二、理论
三、改进
四、算法

一、背景

浅浅学习一下 Marching Cubes 算法（较原始版本），这是将隐式表面提取为显示 mesh 的常见方法。主要基于前辈们的博客和笔记进行整理。主要参考：

二、理论

摘要

Marching cubes （行进立方体）算法可以描述如下：给定一个三维对象，确定任意点是否在三维对象内以及确定三维对象的表面。
将边界内的空间划分为任意数量的立方体。测试每个立方体的顶点是否在对象内部。若一个立方体的某些顶点在对象内，某些顶点在对象外，那该三维对象表面必穿过该立方体。若立方体的一条边的两个端点分别在对象内和对象外，则该边与表面相交。求得相交点，并连接这些交点以在每个立方体中绘制一个表面，则可以对真实的三维对象表面进行拟合。

在2D空间中

为了了解 Marching cubes 算法的工作原理，先以2D案例为例，称之为 Marching Squares 算法。
真实对象如下：
在这里插入图片描述
根据其大致边界将其所在2D空间分块：

判断哪些顶点在对象内部，哪些在对象外部，对其进行标记，红色表示内部，蓝色表示外部：

很容易看出，在内部顶点和外部顶点之间的每条边上的某处，原始表面必与正方形（紫色点）相交：
在这里插入图片描述
让我们连接每个方块的紫色点。得到原始表面的近似值（紫色线）：

现在不将紫色点放在红色和蓝色点中间，计算表面与各个边的实际交点作为紫色点。得到准确的表面。

在3D空间中

在 3D 中实现该算法的工作原理与在 2D 中执行的大致相同。你现在有一堆带有标记角的立方体。对于每个立方体，您知道表面与立方体沿着相对分类的角之间的边缘相交。每个立方体应该看起来像这样：
在这里插入图片描述
在 2D 中，为了近似表面，我们只需在每个紫色点之间画线即可。但在 3D 中，这会给我们一个奇怪的线条图，如下所示：

我们想要做的是对立方体进行三角剖分，其中实心三角形将表示穿过立方体的表面，类似这样：
在这里插入图片描述
但这并不像在一个正方形中画一条连接所有紫色点的线那么容易。一方面，一个三角形连接 3 个点，另一方面，很难辨别哪个三角形连接哪三个点。如果随机连接三角形中的点，可能会得到类似的东西：

另一个问题是，由于要对很多多维数据集执行此操作，如何找到快速的何解决方案。
什么是真正的快？——查询表。
一个立方体有8个顶点，每个顶点可以在对象内部或外部。意味着需要处理 2⁸ 种不同的可能性来确定三角形的外观。幸运的是，实际上只有 15 个独特的三角剖分：
请添加图片描述
每个三角剖分包含零到四个三角形，可以存储为三角形列表，三角形可用其 3 顶点所在的边的索引表示。
在这里插入图片描述
例如，如果顶点 0 的值为负值，而所有其他顶点的值为正值。鉴于我们的等值面为 0，我们可以得出结论，顶点 0 在三维对象外，三维对象与边 0、3 和 8 相交，则这个三角形可以用 [0, 8, 3] 表示。

知道了边的索引，然后根据边的 2 个顶点的实际坐标在边上进行插值，估计交点（估计的顶点可通过沿边插值来计算，或者默认它们的位置在边的中间，插值方式一般会有更光滑的表面）。再连接交点，添加三角形。接着调整立方体的实际全局位置。

迭代所有立方体，将三角形添加到列表中，最终的网格是所有这些三角形的并集。设定的立方体越小，网格三角形就越小，近似值就更接近目标函数。

请添加图片描述

实际上，在创建网格时，（某些程序）会并行处理立方体，而非逐个处理。

三、改进

顶点法线

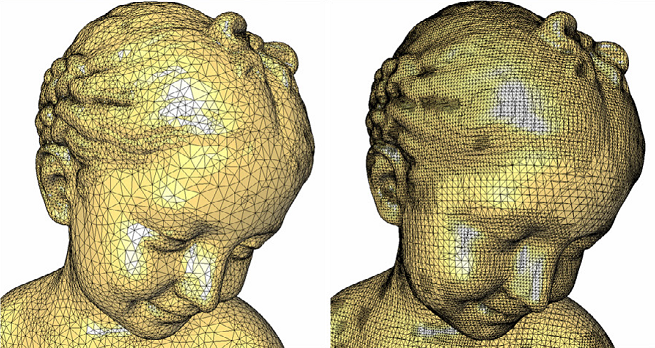
通常需要为三角形面的每个顶点创建法线以实现平滑渲染。最初的论文通过对立方体顶点处的法线进行插值来计算顶点处的法线。这些立方体顶点法线是使用体积数据的中心差分计算的。在创建三角形面后执行此操作的一种方法是对共享三角形顶点的所有面的法线进行平均。如下左图的每个顶点都应用了小平面的单个法线，右图展示了平均法线的平滑结果。
在这里插入图片描述

另一种常见的方法是在每个顶点处使用共享该顶点的多边形法线的加权平均值。权重是多边形面积的倒数，因此小的多边形具有更大的权重。这个想法是小多边形可能出现在高表面曲率的区域。
在这里插入图片描述

多分辨率

更智能的行进立方体形式会调整其立方体分辨率以匹配局部表面复杂性，但生成的网格质量相当低。作为比较，在下图中，右侧网格是使用行进立方体制作的，而左侧网格是 Variational Reconstruction 制作的。
在这里插入图片描述

经典行进立方体方法简单实用。且隐式函数在计算机图形学和其他领域经常出现，很多地方都直接使用的经典行进立方体方法。

行进四面体

基本思想与“移动立方体”算法一致，其基本采样结构是一个四面体。
每个立方体网格单元被分成 6 个四面体，四面体边缘与相邻盒子单元格上的边缘对齐。为每个四面体独立计算等值面的平面小平面近似值。小平面顶点通过线性插值确定，其中等值面切割四面体的边缘。

在这里插入图片描述
有 8 种不同的情况。其中7中为四面体顶点处的空心圆和实心圆表示顶点位于等值面的不同侧。还有一种是所有顶点都在等值面上方或下方，在这种情况下不会生成小平面。

在这里插入图片描述

这种技术不会受到传统行进立方体算法中的歧义的影响。
由于这是离散采样，因此如果等值面在单元内变化，则可能会错过部分等值面。这是任何离散采样数据集中的标准问题，必须满足奈奎斯特准则。
如果切面的方向很重要（顺时针或逆时针），那么就需要对上述相同的情况进行单独处理。每一对的切面都有相同的顶点，但根据被多边形化的对象的 “内部” 是高值还是低值而有不同的排序。

深度学习

较近的，有用深度学习方法（2021 NMC）进行改进的，效果看上去不错，这里暂不展开，有兴趣可移步原文。

在这里插入图片描述

四、算法

最后简单看一下sdfstudio中的 marching_cubes 。

from pathlib import Path

import numpy as np
import pymeshlab
import torch
import trimesh
from skimage import measure

avg_pool_3d = torch.nn.AvgPool3d(2, stride=2)
upsample = torch.nn.Upsample(scale_factor=2, mode="nearest")
max_pool_3d = torch.nn.MaxPool3d(3, stride=1, padding=1)

def get_surface_sliding(
    sdf,
    resolution=512,
    bounding_box_min=(-1.0, -1.0, -1.0),
    bounding_box_max=(1.0, 1.0, 1.0),
    return_mesh=False,
    level=0,
    coarse_mask=None,
    output_path: Path = Path("test.ply"),
    simplify_mesh=True,
):
    assert resolution % 512 == 0
    if coarse_mask is not None:
        # we need to permute here as pytorch's grid_sample use (z, y, x)
        coarse_mask = coarse_mask.permute(2, 1, 0)[None, None].cuda().float()

    resN = resolution   
    cropN = 512
    level = 0
    N = resN // cropN		#数除法运算符，用于执行整数除法运算并返回结果的整数部分

    grid_min = bounding_box_min
    grid_max = bounding_box_max
    xs = np.linspace(grid_min[0], grid_max[0], N + 1)
    ys = np.linspace(grid_min[1], grid_max[1], N + 1)
    zs = np.linspace(grid_min[2], grid_max[2], N + 1)

    # print(xs)
    # print(ys)
    # print(zs)
    meshes = []
    # 三层循环，三个维度的行进过程
    for i in range(N):
        for j in range(N):
            for k in range(N):
                # print(i, j, k)
                x_min, x_max = xs[i], xs[i + 1]
                y_min, y_max = ys[j], ys[j + 1]
                z_min, z_max = zs[k], zs[k + 1]

                x = np.linspace(x_min, x_max, cropN)
                y = np.linspace(y_min, y_max, cropN)
                z = np.linspace(z_min, z_max, cropN)

                xx, yy, zz = np.meshgrid(x, y, z, indexing="ij")
                points = torch.tensor(np.vstack([xx.ravel(), yy.ravel(), zz.ravel()]).T, dtype=torch.float).cuda()

                def evaluate(points):
                    z = []
                    for _, pnts in enumerate(torch.split(points, 100000, dim=0)):
                        z.append(sdf(pnts))		#根据顶点估计sdf值
                    z = torch.cat(z, axis=0)	
                    return z

                # construct point pyramids	构建点金字塔
                # 将points重塑为一个四维数组，并重新排列维度顺序为 (3, cropN, cropN, cropN)。
                points = points.reshape(cropN, cropN, cropN, 3).permute(3, 0, 1, 2)
                if coarse_mask is not None:
                    # breakpoint()
                    points_tmp = points.permute(1, 2, 3, 0)[None].cuda()
                    current_mask = torch.nn.functional.grid_sample(coarse_mask, points_tmp)
                    current_mask = (current_mask > 0.0).cpu().numpy()[0, 0]
                else:
                    current_mask = None

                points_pyramid = [points]
                for _ in range(3):
                    points = avg_pool_3d(points[None])[0]
                    points_pyramid.append(points)
                points_pyramid = points_pyramid[::-1]

                # evalute pyramid with mask
                mask = None
                threshold = 2 * (x_max - x_min) / cropN * 8
                for pid, pts in enumerate(points_pyramid):
                    coarse_N = pts.shape[-1]
                    pts = pts.reshape(3, -1).permute(1, 0).contiguous()		# (N, 3)

                    if mask is None:
                        # only evaluate
                        if coarse_mask is not None:
                            pts_sdf = torch.ones_like(pts[:, 1])
                            valid_mask = (
                                torch.nn.functional.grid_sample(coarse_mask, pts[None, None, None])[0, 0, 0, 0] > 0
                            )
                            if valid_mask.any():
                                pts_sdf[valid_mask] = evaluate(pts[valid_mask].contiguous())
                        else:
                            pts_sdf = evaluate(pts)		# 估计出每个顶点的sdf值
                    else:
                        mask = mask.reshape(-1)
                        pts_to_eval = pts[mask]

                        if pts_to_eval.shape[0] > 0:
                            pts_sdf_eval = evaluate(pts_to_eval.contiguous())
                            pts_sdf[mask] = pts_sdf_eval
                        # print("ratio", pts_to_eval.shape[0] / pts.shape[0])

                    if pid < 3:
                        # update mask
                        mask = torch.abs(pts_sdf) < threshold
                        mask = mask.reshape(coarse_N, coarse_N, coarse_N)[None, None]
                        mask = upsample(mask.float()).bool()

                        pts_sdf = pts_sdf.reshape(coarse_N, coarse_N, coarse_N)[None, None]
                        pts_sdf = upsample(pts_sdf)
                        pts_sdf = pts_sdf.reshape(-1)

                    threshold /= 2.0

                z = pts_sdf.detach().cpu().numpy()

                # skip if no surface found
                if current_mask is not None:
                    valid_z = z.reshape(cropN, cropN, cropN)[current_mask]
                    if valid_z.shape[0] <= 0 or (np.min(valid_z) > level or np.max(valid_z) < level):		
                        continue

                if not (np.min(z) > level or np.max(z) < level):	# 顶点都为正或负
                    z = z.astype(np.float32)
                    # 在这一步正式使用 marching_cubes 估计三角形面及法线
                    verts, faces, normals, _ = measure.marching_cubes(
                        volume=z.reshape(cropN, cropN, cropN),  # .transpose([1, 0, 2]),
                        level=level,
                        spacing=(
                            (x_max - x_min) / (cropN - 1),
                            (y_max - y_min) / (cropN - 1),
                            (z_max - z_min) / (cropN - 1),
                        ),
                        mask=current_mask,
                    )
                    # print(np.array([x_min, y_min, z_min]))
                    # print(verts.min(), verts.max())
                    verts = verts + np.array([x_min, y_min, z_min])		# 计算顶点的实际位置
                    # print(verts.min(), verts.max())

                    meshcrop = trimesh.Trimesh(verts, faces, normals)	# 构建 mesh
                    # meshcrop.export(f"{i}_{j}_{k}.ply")
                    meshes.append(meshcrop)

    combined = trimesh.util.concatenate(meshes)		# 合并所有三角形面

	# 导出
    if return_mesh:
        return combined
    else:
        filename = str(output_path)
        filename_simplify = str(output_path).replace(".ply", "-simplify.ply")
        combined.merge_vertices(digits_vertex=6)
        combined.export(filename)
        if simplify_mesh:		# 简化
            ms = pymeshlab.MeshSet()
            ms.load_new_mesh(filename)

            print("simply mesh")
            ms.meshing_decimation_quadric_edge_collapse(targetfacenum=2000000)
            ms.save_current_mesh(filename_simplify, save_face_color=False)

其中，skimage.measure.marching_cubes 基于经典方法实现。

def marching_cubes(volume, level, spacing=(1., 1., 1.),
                   gradient_direction='descent'):
    """
    Marching cubes algorithm to find iso-valued surfaces in 3d volumetric data

    Parameters
    ----------
    volume : (M, N, P) array of doubles
        Input data volume to find isosurfaces. Will be cast to `np.float64`.
    level : float
        Contour value to search for isosurfaces in `volume`.
    spacing : length-3 tuple of floats
        Voxel spacing in spatial dimensions corresponding to numpy array
        indexing dimensions (M, N, P) as in `volume`.
    gradient_direction : string
        Controls if the mesh was generated from an isosurface with gradient
        descent toward objects of interest (the default), or the opposite.
        The two options are:
        * descent : Object was greater than exterior
        * ascent : Exterior was greater than object

    Returns
    -------
    verts : (V, 3) array
        Spatial coordinates for V unique mesh vertices. Coordinate order
        matches input `volume` (M, N, P).
    faces : (F, 3) array
        Define triangular faces via referencing vertex indices from ``verts``.
        This algorithm specifically outputs triangles, so each face has
        exactly three indices.