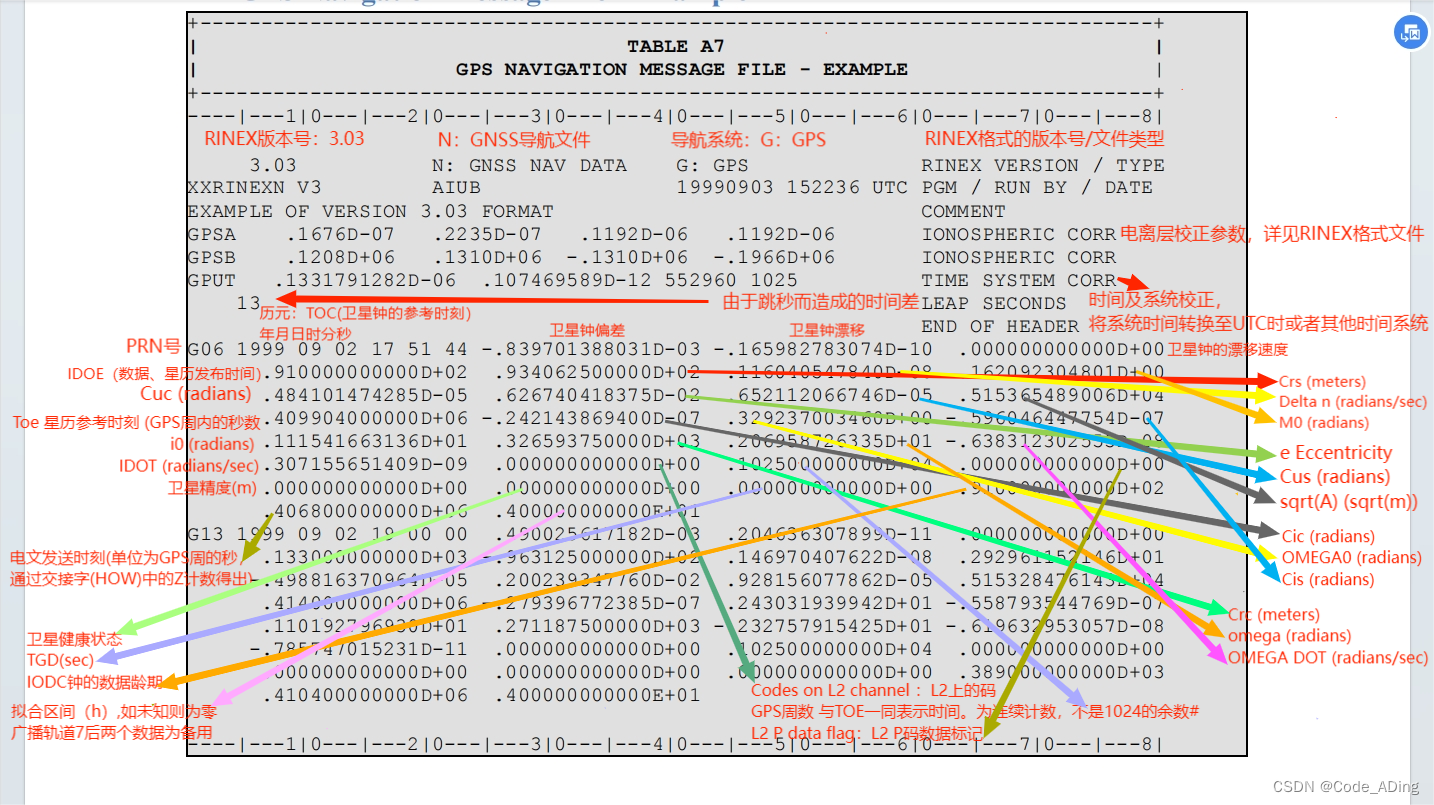
使用广播星历进行 GPS 卫星位置的计算

目录1.计算卫星运动的平均角速度 n2.计算观测瞬间卫星的近地点角3.计算偏近点角4.计算真近点角 f5.计算升交角距 6.计算摄动改正项7.进行摄动改正 8.计算卫星在轨道面坐标系中的位置9.计算观测瞬间升交点的经度 L10.计算卫星在瞬时地球坐标系中的位置11.计算卫星在协议地球坐标系中的位置使用广播星历进行GPS卫星位置的计算的详细步骤如下：关于在广播星历中各参数的分布情况可以参考下图：首先

Code_ADing

3302人浏览 · 2023-12-15 18:40:18

Code_ADing · 2023-12-15 18:40:18 发布

使用广播星历进行GPS卫星位置的计算的详细步骤如下：

关于在广播星历中各参数的分布情况可以参考下图：

1.计算卫星运动的平均角速度 n

首先根据广播星历中给出的参数 $\sqrt{A}$ 计算参考时刻(TOE) $t_{oe}$ 的平均角速度 $n_{0}$

$n_{0} = \frac{\sqrt{GM}}{(\sqrt{A})^{3}}$

式中，GM为万有引力常数 G 与地球总质量 M 之乘积，其值为 $GM = 3.986005 \times 10^{14} m^{3} / s^{2}$ 然后根据广播星历中给定的摄动参数 $\Delta n$ 计算观测时刻卫星的平均角速度 n

$n = n_{0} + \Delta n$

注：观测时刻：地面站观测的时间；参考时刻：卫星发出信号的时间

2.计算观测瞬间卫星的近地点角

式中， $M_{0}$ 为参考时刻 $t_{oe}$ 时的平近点角，由广播星历给出。

问：为什么要用参考时刻 $t_{oe}$ 来替代卫星过近地点时刻 $t_{0}$ 来计算呢?

答：因为广播星历每 2h 更新一次，将参考时刻设在中央时刻时，外推间隔小于等于 1h。而卫星的运行周期为 12h 左右，采用卫星过近地点时刻 $t_{0}$ 来计算时，外推间隔最大有可能达 6h 。用 $t_{oe}$ 来取代卫星过近地点时刻 $t_{0}$ 后，外推间隔将大大减小，用较简单的模型也能获得精度较高的结果。

3.计算偏近点角

用弧度表示的开普勒方程为：

用角度表示的开普勒方程为：

解上述方程可用迭代法或微分改正法。

4.计算真近点角 f

式中，e 为卫星轨道的偏心率，由广播星历给出。

所以，真近点角 f 可以表示为：

5.计算升交角距 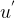$u^{'}$

式中， $\omega$ 为近地点角距，由广播星历给出。

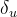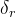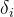
6.计算摄动改正项 $\delta _{u}$ 、 $\delta _{r}$ 、 $\delta _{i}$

广播星历中给出了下列6个摄动参数：

据此可以求出引起的升交角距 u 的摄动改正项 $\delta _{u}$ 、卫星矢径 r 的摄动改正项 $\delta _{r}$ 和卫星轨道倾角 i 的摄动改正项 $\delta _{i}$ 。

卫星矢径 r ：接收机与卫星之间的绝对距离（直线距离），以米为单位。

计算公式如下:

7.对 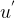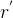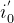$u^{'}$ 、 $r^{'}$ 、 $i_{0}^{'}$ 进行摄动改正

式中，a 为卫星轨道的长半径，a = $(\sqrt{A})^{2}$ ， $\sqrt{A}$ 由广播星历给出；

$i_{0}$ 为 $t_{oe}$ 时刻的轨道倾角，由广播星历中的开普勒六参数给出；

$\frac{di}{dt}$ 为轨道倾角 i 的变化率，由广播星历中的摄动九参数给出。

8.计算卫星在轨道面坐标系中的位置

在轨道平面直角坐标系中(坐标原点位于地心, 轴指向升交点)，

卫星的平面直角坐标为:

卫星矢径 r 、升交角距 u

9.计算观测瞬间升交点的经度 L

设参考时刻 $t_{oe}$ 时升交点的赤经为 $\Omega _{t_{oe}}$ , 升交点对时间的变化率为 $\dot{\Omega }$ ，

那么观测瞬间 t 的升交点赤经 $\Omega$ 应为:

$\dot{\Omega }$ 可从广播星历的摄动参数中给出。

设本周开始时刻(星期日 0 时)格林尼治恒星时为 $GAST_{week}$ ，则观测瞬间的格林尼治恒星时为：

其中， $\omega _{e}$ 为地球自转角速度，其值为 $\omega _{e} = 7.292115 \times 10^{-5} rad/s$

t 为本周内的时间(s)，从本周开始时刻起算至本周观测时刻瞬间的秒数

显然，上述算法中把地球自转看成是完全匀速的，未顾及地球自转的不均匀性。

这样就可以求得观测瞬间升交点的经度值 L ：

令：

则有：

注意：广播星历中给出的并不是参考时刻 $t_{oe}$ 的升交点赤经 $\Omega _{t_{oe}}$ ，而是该值与本周起始时刻的格林尼治恒星时 $GAST_{week}$ 之差(即上述的 $\Omega _{0}$ )。

10.计算卫星在瞬时地球坐标系中的位置

已知升交点的大地经度 L 以及轨道平面的倾角 i 后，

就可通过两次旋转方便地求得卫星在地固坐标系中的位置：

11.计算卫星在协议地球坐标系中的位置

观测瞬间卫星在协议地球坐标系中的位置为：

在GPS定位中，常常需要多次计算卫星的位置和速度如用上述方法计算需占用较多的内存和计算时间。为此，常将卫星星历用一个时间多项式来表示，在内存中仅保存该多项式的系数，供计算时调用。

在各种多项式中，切比雪夫多项式的拟合效果最佳，即使在该时间段的两端近似性也很好。用 n 阶切比雪夫多项式来逼近时间段 $\left [t_{0} , t_{0} + \Delta t \right ]$ 中的卫星星历时，先将变量 $t \epsilon \left [t_{0} , t_{0} + \Delta t \right ]$ 变换为变量 $\tau \epsilon \left [-1,1\right ]$ ：