在大数运算中，比较难实现的应该是高精度/高精度的除法器。

目录

一、原理

二、具体代码解析

三、超长整数运算

---

一、原理

1.大数存储

        先说说大数在C语言程序中是怎么存储的。我们使用长度为N的int数组来存储无符号超长整数，其中数组每个元素存储的值上限为M。如下：       

#define M 10000	//M进制，int数组每个元素取值上限
#define N 5		//数组长度
int x[N]={0};

         因为int类型最多表示10位有效数字（最大值为2147483648），当两个有效位数为5的int类型变量相乘时其结果可能溢出，为了便于乘法器的实现M取值最好小于10000 

        举个例子，当我们要用x存储一个无符号超长整数6543210435135314时，数组x的值是这样的：x[0]=5314,x[1]=3513,x[2]=2104,x[3]=6543,x[4]=0。

2.除法算法

除法操作数的关系如下:

        被除数/除数=商......余数，其中被除数=商*除数+余数

首先除数不能为0；

当被除数为0时，商为0；

当被除数小于除数时，商为0，余数为被除数；

当被除数等于除数时，商为1，余数为0;

 ……

1)日常生活中，我们是这样算除法的：

 

2）但是在大数除法中，我们不能直接这么算。例如：对于1234 5678 9000 / 1 2345，计算机没法直接计算1234 5678 / 1 2345的结果。

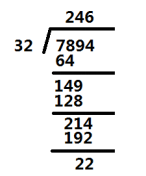
3）在计算机中，减法的实现要比除法简单得多，因此我们考虑把除法转变成减法来计算。例如：对于7894/32，我们有：

 

通过被除数不断地减去除数，我们得到了余数22，而除数被减的次数就是商246。 

4）现在我们已经知道了如何在计算机中把除法转变成减法来运算，但一个除数一个除数的减实在太慢了，那么有没有更快的算法呢？答案是肯定的，我们可以通过移位来加快“减”的速度，例如：

 

 如图，7894=32*2*100+32*4*10+32*6*1+22，一共减去了2*100+4*10+6*1=246个32，所以7894/32的商为246。

---

二、具体代码解析

1.首先函数原型如下：

#define M 10000	//M进制，int数组每个元素取值上限
#define N 5		//数组长度
int div2(int n1[],int n2[],int quotient[]);
/*	大数除法：无符号高精度整数/无符号高精度整数，n1为被除数，n2为除数，quotient为商。函数正确执行时返回整数1	*/

此外还涉及到这些函数： 

int add(int num1[],int num2[],int sum[]);	
/* 大数加法 */ 
int sub(int num1[],int num2[],int difference[]);
/* 大数减法 */ 
int mul(int num1[],int num2[],int product[]);
/* 大数乘法 */
int div(int num1[],int num2,int quotient[]);
/* 大数除法：无符号高精度整数/无符号低精度整数，其中num2>0且num2<=M */ 
int cmp(int num1[],int num2[]);	
/* 大数比较，num1>num2时return1，小于时返回-1，等于时返回0 */ 

 2.异常值处理

        因为我们这里存储的是无符号超长整数，参与运算的操作数也应该是无符号，并且数组的每个元素应该小于M。所以有： 

int div2(int n1[],int n2[],int quotient[]){
int i=0;
int num1[N]={0},num2[N]={0};
	for(i=0;i<N;i++){
//异常值处理
		if(n1[i]<0||n2[i]<0||n1[i]>=M||n2[i]>=M){
			printf("div2():Operand are forbidden!\n");
			return -2;
		}
//初始化：
       num1[i]=n1[i];
		num2[i]=n2[i];
		quotient[i]=0;
}
return 1;//运算正确
}

        这里说明一下为什么函数不直接用n1、n2参与运算，这是因为这个函数div2传递的参数都是指针，而接下来的算法将会改变被除数的值。为防止函数结束后被除数的值被改变，所以新定义了和n1、n2值相等的两个局部变量num1、num2。

3.特殊值处理

        包含以下特殊情况的处理： （1）首先除数不能为0；（2）当被除数为0时，商为0；（3）当被除数小于除数时，商为0；（4）当被除数等于除数时，商为1。

 /*----特殊值处理----*/
    //检查除数是否为0
    for(i=N-1;i>=0&&(num2[i]==0);i--);//从高位开始寻找num2首个不为0的下标
    if(i<0){
        printf("除数不能为0\n");
        return -1;
    }
    //被除数小于除数
    if((flag=cmp(num1,num2))==-1){
        quotient[0]=0;
        return 1;
    }
    //被除数等于除数
    else if(flag==0){
        quotient[0]=1;
        return 1;
    }
/*---特殊值处理end---*/

 //别忘了在前面声明flag!

4.处理完上述特殊情况，剩下的就是被除数大于除数的情况了，从这里开始就是算法的核心部分。

        首先，为了加快减的速度，我们要尽可能地把除数左移。因为M取值10000，num2[i]有效位数为4，我们先4位(十进制位)4位(十进制位)的左移，直到除数num2大于被除数num1时停止。接下来把除数1位(十进制位)1位(十进制位)地右移，直到num1>num2时停止。这时，被除数num1刚好大于除数num2。 

/*---计算除数最大移位---*/
    if(num2[N-1]>0)
        flag=0;//flag=0表示除数不能移位,因为最高位>0

    for(counts=0;counts<N&&(flag>0);){
        //num2左移4位:
        for(i=N-1;i>0;i--)
            num2[i]=num2[i-1];
        num2[0]=0;
        counts++;//左移次数+4，counts+1
        flag=cmp(num1,num2);
    }
    counts=counts*4;
    for(i=0;i<counts&&(cmp(num1,num2)<0);i++){
        if(div(num2,10,num2)!=1) return -1;//如果除数num2大于被除数num1，右移1位
    }
    counts=counts-i;//此时counts为除数左移位数
/*--计算除数最大移位end--*/

//这里左移一个10进制位是用高精度整数/低精度整数除法div实现的

//counts为num2左移位数(十进制位)，别忘了在前面声明!

5.计算被除数减去除数的次数

for(;counts>=0;counts--){
    if(cmp(num1,num2)>=0){
        //除数num2左移counts位时,num1最多能减去num2的次数times：
        for(times=0;times<M&&(cmp(num1,num2)>=0);times++){
            sub(num1,num2,num1);
			}
        //除数num2左移counts位时,被除数最多能减去除数t=times*(10^counts)次：
		for(i=0;i<N;i++)
		{t[i]=0;m[i]=0;}//初始化t、m
		t[0]=times;
		m[0]=10;
		for(i=0;i<counts;i++){
			if(mul(t,m,t)!=1)
				return -1;
		}
        //“减”的次数：
		if(add(quotient,t,quotient)!=1) return -1;
	}
    if(div(num2,10,num2)!=1) return -1;//除数右移1位
}

 //别忘了在前面声明times、t、m!

6.完整的div2函数定义如下：

#define M 10000	//M进制，int数组每个元素取值上限
#define N 5		//数组长度
//函数声明：
int add(int num1[],int num2[],int sum[]);
int cmp(int num1[],int num2[]);
int sub(int num1[],int num2[],int difference[]);
int mul(int num1[],int num2[],int product[]);
int div(int num1[],int num2,int quotient[]);
/*
===无符号超长整数 除法===
quotient=n1/n2
高精度整数/高精度整数
*/
int div2(int n1[],int n2[],int quotient[]){
    int i=0,flag=1,counts=0,times=0;
	int t[N]={0},m[N]={0},num1[N]={0},num2[N]={0};
	for(i=0;i<N;i++){
        //异常值处理
		if(n1[i]<0||n2[i]<0||n1[i]>=M||n2[i]>=M){
			printf("div2():Operand are forbidden!\n");
			return -2;
		}
        //初始化：
        num1[i]=n1[i];
		num2[i]=n2[i];
		quotient[i]=0;
    }

    /*----特殊值处理----*/
    //检查除数是否为0
    for(i=N-1;i>=0&&(num2[i]==0);i--);//从高位开始寻找num2首个不为0的下标
    if(i<0){
        printf("除数不能为0\n");
        return -1;
    }
    //被除数小于除数
    if((flag=cmp(num1,num2))==-1){
        quotient[0]=0;
        return 1;
    }
    //被除数等于除数
    else if(flag==0){
        quotient[0]=1;
        return 1;
    }
    /*---特殊值处理end---*/

    /*---计算除数最大移位---*/
    if(num2[N-1]>0)
        flag=0;//flag=0表示除数不能移位,因为最高位>0
    for(counts=0;counts<N&&(flag>0);){
        //num2左移4位:
        for(i=N-1;i>0;i--)
            num2[i]=num2[i-1];
        num2[0]=0;
        counts++;//左移次数+4，counts+1
        flag=cmp(num1,num2);
    }
    counts=counts*4;
    for(i=0;i<counts&&(cmp(num1,num2)<0);i++){
        if(div(num2,10,num2)!=1) return -1;//如果除数num2大于被除数num1，右移1位
    }
    counts=counts-i;//此时counts为除数左移位数
    /*--计算除数最大移位end--*/

    for(;counts>=0;counts--){
        if(cmp(num1,num2)>=0){
            //除数num2左移counts位时,num1最多能减去num2的次数times：
            for(times=0;times<M&&(cmp(num1,num2)>=0);times++){
                sub(num1,num2,num1);
            }
            //除数num2左移counts位时,被除数最多能减去除数t=times*(10^counts)次：
            for(i=0;i<N;i++)
            {t[i]=0;m[i]=0;}//初始化t、m
            t[0]=times;
            m[0]=10;
            for(i=0;i<counts;i++){
                if(mul(t,m,t)!=1)
                    return -1;
            }
            //“减”的次数：
            if(add(quotient,t,quotient)!=1) return -1;
        }
        if(div(num2,10,num2)!=1) return -1;//除数右移1位
    }
    return 1;//运算正确
}

---

三、超长整数运算

        如果需要大数运算的完整代码（包括输入输出、加减乘除函数），可以参考我的另一篇文章：超长整数运算——从斐波那契数列说起 的<无符号超长整数运算>部分。