💥💥💥💥💥💥💞💞💞💞💞💞💞💞欢迎来到海神之光博客之家💞💞💞💞💞💞💞💞💥💥💥💥💥💥

✅博主简介：热爱科研的Matlab仿真开发者，修心和技术同步精进；
🍎个人主页：海神之光
🏆代码获取方式：
海神之光Matlab王者学习之路—代码获取方式

⛳️座右铭：行百里者，半于九十。
更多Matlab路径规划仿真内容点击👇
①Matlab路径规划（进阶版）
②付费专栏Matlab路径规划（初级版）

⛳️关注CSDN海神之光，更多资源等你来！！

⛄一、简介

人工势场法是局部路径规划的一种比较常用的方法。这种方法假设机器人在一种虚拟力场下运动。

如图所示，机器人在一个二维环境下运动，图中指出了机器人，障碍和目标之间的相对位置。

这个图比较清晰的说明了人工势场法的作用，物体的初始点在一个较高的“山头”上，要到达的目标点在“山脚”下，这就形成了一种势场，物体在这种势的引导下，避开障碍物，到达目标点。

人工势场包括引力场合斥力场，其中目标点对物体产生引力，引导物体朝向其运动（这一点有点类似于A*算法中的启发函数h）。障碍物对物体产生斥力，避免物体与之发生碰撞。物体在路径上每一点所受的合力等于这一点所有斥力和引力的和。这里的关键是如何构建引力场和斥力场。下面我们分别讨论一下：

引力场：

常用的引力函数：

这里的ε是尺度因子.ρ(q,q_goal)表示物体当前状态与目标的距离。引力场有了，那么引力就是引力场对距离的导数（类比物理里面W=FX）：、

关于梯度的算法可以参考相关资料，简单提一下，二元函数梯度是酱紫的[δx,δy],这个符号是偏导数，不太对，见谅。

Fig .引力场模型

斥力场：

公式（3）是传统的斥力场公式，现在还没有搞清楚是怎么推导出来的。公式中η是斥力尺度因子，ρ（q,q_obs）代表物体和障碍物之间的距离。ρ_0代表每个障碍物的影响半径。换言之，离开一定的距离，障碍物就对物体没有斥力影响。

斥力就是斥力场的梯度


Fig 斥力场模型

总的场就是斥力场合引力场的叠加，也就是U=U_att+U_rep,总的力也是对对应的分力的叠加，如下图所示：

二、存在的问题
（a） 当物体离目标点比较远时，引力将变的特别大，相对较小的斥力在甚至可以忽略的情况下，物体路径上可能会碰到障碍物

（b）当目标点附近有障碍物时，斥力将非常大，引力相对较小，物体很难到达目标点

（c）在某个点，引力和斥力刚好大小相等，方向想反，则物体容易陷入局部最优解或震荡

三、各种改进版本的人工势场法
（a）对于可能会碰到障碍物的问题，可以通过修正引力函数来解决，避免由于离目标点太远导致引力过大

和（1）式相比，（5）式增加了范围限定。d*_goal 给定了一个阈值限定了目标和物体之间的距离。对应的梯度也就是引力相应变成：

（b）目标点附近有障碍物导致目标不可达的问题，引入一种新的斥力函数

这里在原有斥力场的基础上，加上了目标和物体距离的影响,（n是正数，我看到有篇文献上n=2）。直观上来说，物体靠近目标时，虽然斥力场要增大，但是距离在减少，所以在一定程度上可以起到对斥力场的拖拽作用

相应斥力变成：

所以可以看到这里引力分为两个部分，编程时要格外注意

（c）局部最优问题是一个人工势场法的一个大问题，这里可以通过加一个随机扰动，让物体跳出局部最优值。类似于梯度下降法局部最优值的解决方案。

⛄二、部分源代码

clear all;
%障碍和目标，起始位置都已知的路径规划,意图实现从起点可以规划出一条避开障碍到达目标的路径。
%初始化车的参数
Xo=[0 0];% 起点位置
k=1000;% 计算引力需要的增益系数
%K=0;% 初始化
m=10;% 计算斥力的增益系数，都是自己设定的。
Po=1;%障碍影响距离，当障碍和车的距离大于这个距离时，斥力为0，即不受该障碍的影响。也是自己设定。
n=9;%障碍个数
a=0.5;
l=0.1;% 步长
J=300;%循环迭代次数
r = 0.5;
%如果不能实现预期目标，可能也与初始的增益系数， Po 设置的不合适有关。
%end
%给出障碍和目标信息
Xsum=[10 10;1 1.5;3 2.2;4 4.5;3 6;6 2.5;5.5 6; 6 4.5;9 9;8.5 5];% 这个向量是(n+1)2 维，其中[10 10] 是目标位置，剩下的都是障碍的位置。
Xj=Xo;%j=1 循环初始，将车的起始坐标赋给Xj
%************** 初始化结束，开始主体循环******************
for j=1:J% 循环开始
Goal(j,1)=Xj(1);%Goal 是保存车走过的每个点的坐标。刚开始先将起点放进该向量。
Goal(j,2)=Xj(2);
%调用计算角度模块
Theta=compute_angle(Xj,Xsum,n);%Theta 是计算出来的车和障碍，和目标之间的与X 轴之间的夹角，统一规定角度为逆时针方向，用这个模块可以计算出来。
%调用计算引力模块
Angle=Theta(1);%Theta （1）是车和目标之间的角度，目标对车是引力。
angle_at=Theta(1);% 为了后续计算斥力在引力方向的分量赋值给angle_at
[Fatx,Faty]=compute_Attract(Xj,Xsum,k,Angle,0,Po,n);% 计算出目标对车的引力在x,y 方向的两个分量值。
for i=1:n
angle_re(i)=Theta(i+1);% 计算斥力用的角度，是个向量，因为有n 个障碍，就有n 个角度。
end
%调用计算斥力模块
[Frerxx,Freryy,Fataxx,Fatayy]=compute_repulsion(Xj,Xsum,m,angle_at,angle_re,n,Po,a,r);%计算出斥力在x,y 方向的分量数组。
%计算合力和方向，这有问题，应该是数，每个j 循环的时候合力的大小应该是一个唯一的数，不是数组。应该把斥力的所有分量相加，引力所有分量相加。
Fsumyj=Faty+Freryy+Fatayy;%y 方向的合力
Fsumxj=Fatx+Frerxx+Fataxx;%x 方向的合力
Position_angle(j)=atan(Fsumyj/Fsumxj);% 合力与x 轴方向的夹角向量
%计算车的下一步位置

%保存车的每一个位置在向量中
Xj=Xnext;
%判断
if ((Xj(1)-Xsum(1,1))>0)&((Xj(2)-Xsum(1,2))>0)% 是应该完全相等的时候算作到达， 还是只是接近就可以？现在按完全相等的时候编程。
    K=j  % 记录迭代到多少次，到达目标。
break;
%记录此时的j 值
end%如果不符合if 的条件，重新返回循环，继续执行。

end%大循环结束
K=j;
Goal(K,1)=Xsum(1,1);% 把路径向量的最后一个点赋值为目标
Goal(K,2)=Xsum(1,2);
%*********************************** 画出障碍， 起点， 目标， 路径点*************************
%画出路径

%路径向量Goal 是二维数组,X,Y 分别是数组的x,y 元素的集合，是两个一维数组。
x=[1 3 4 3 6 5.5 6 9 8.5];% 障碍的x 坐标
y=[1.5 2.2 4.5 6 2.5 6 4.5 9 5];
plot(10,10,‘v’,0,0,‘ms’,X,Y ,‘-k’,‘linewidth’,3);

Pathkm = Kl
%斥力计算
function [Yrerxx,Yreryy,Yataxx,Yatayy]=compute_repulsion(X,Xsum,m,angle_at,angle_re,n,Po,a,r)% 输入参数为当前坐标， Xsum 是目标和障碍的坐标向量，增益常数,障碍，目标方向的角度
Rat=(X(1)-Xsum(1,1))^{2+(X(2)-Xsum(1,2))}2;% 路径点和目标的距离平方
rat=sqrt(Rat);% 路径点和目标的距离
for i=1:n
Rrei(i)=(X(1)-Xsum(i+1,1))^{2+(X(2)-Xsum(i+1,2))}2;% 路径点和障碍的距离平方
rre(i)=sqrt(Rrei(i))-r;% 路径点和障碍的距离保存在数组rrei 中
R0=(Xsum(1,1)-Xsum(i+1,1))^{2+(Xsum(1,2)-Xsum(i+1,2))}2;
r0=sqrt(R0)-r;
if rre(i)>Po% 如果每个障碍和路径的距离大于障碍影响距离，斥力令为0
Yrerx(i)=0;
Yrery(i)=0;
Yatax(i)=0;
Yatay(i)=0;
else
%if r0<Po
if rre(i)<Po/2
if X(2)>Xsum(i+1,2)
Yrer(i)=m(1/rre(i)-1/Po)((1/rre(i))^2)(rat);% 分解的Fre1 向量
Yata(i)=am((1/rre(i)-1/Po)^2)*(rata);% 分解的Fre2 向量
Yrerx(i)=-Yrer(i)cos(angle_re(i));%angle_re(i)=Y(i+1)
Yrery(i)=1Yrer(i)sin(angle_re(i));
Yatax(i)=Yata(i)cos(angle_at);%angle_at=Y(1)
Yatay(i)=Yata(i)sin(angle_at);
else
Yrer(i)=m(1/rre(i)-1/Po)((1/rre(i))^2)(rat);% 分解的Fre1 向量
Yata(i)=am((1/rre(i)-1/Po)^2)*(rata);% 分解的Fre2 向量
Yrerx(i)=Yrer(i)cos(angle_re(i));%angle_re(i)=Y(i+1)
Yrery(i)=-1Yrer(i)sin(angle_re(i));
Yatax(i)=Yata(i)cos(angle_at);%angle_at=Y(1)
Yatay(i)=Yata(i)sin(angle_at);
end
else
if X(2)>Xsum(i+1,2)
Yrer(i)=m(1/rre(i)-1/Po)((1/rre(i))^2)(rat);% 分解的Fre1 向量
Yata(i)=am((1/rre(i)-1/Po)^2)*(rata);% 分解的Fre2 向量
Yrerx(i)=-Yrer(i)cos(angle_re(i));%angle_re(i)=Y(i+1)
Yrery(i)=1Yrer(i)sin(angle_re(i));
Yatax(i)=Yata(i)cos(angle_at);%angle_at=Y(1)
Yatay(i)=Yata(i)sin(angle_at);
else
Yrer(i)=m(1/rre(i)-1/Po)((1/rre(i))^2)Rat;% 分解的Fre1 向量
Yata(i)=am((1/rre(i)-1/Po)^2)*rat;% 分解的Fre2 向量
Yrerx(i)=Yrer(i)*cos(angle_re(i));%angle_re(i)=Y(i+1)
Yrery(i)=Yrer(i)*sin(angle_re(i));
Yatax(i)=Yata(i)*cos(angle_at);%angle_at=Y(1)
Yatay(i)=Yata(i)*sin(angle_at);
end
end

end%判断距离是否在障碍影响范围内

end
Yrerxx=sum(Yrerx);% 叠加斥力的分量
Yreryy=sum(Yrery);
Yataxx=sum(Yatax);
Yatayy=sum(Yatay);

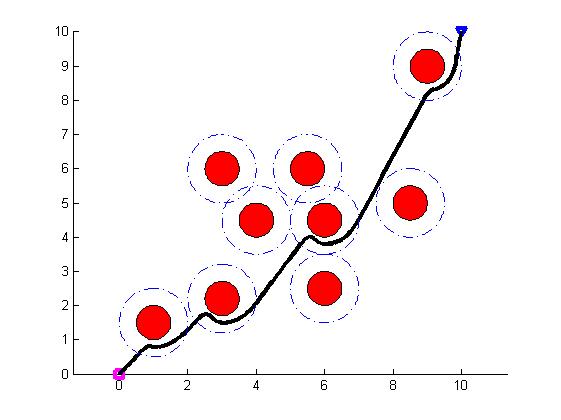
⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]焦阳.基于改进蚁群算法的无人机三维路径规划研究[J].舰船电子工程. 2019,39(03)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除

🍅 仿真咨询
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面
卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

3 图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

4 路径规划方面
旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

5 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配

6 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

7 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

8 电力系统方面
微电网优化、无功优化、配电网重构、储能配置

9 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长

10 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合