点击进入 👉GitHub地址

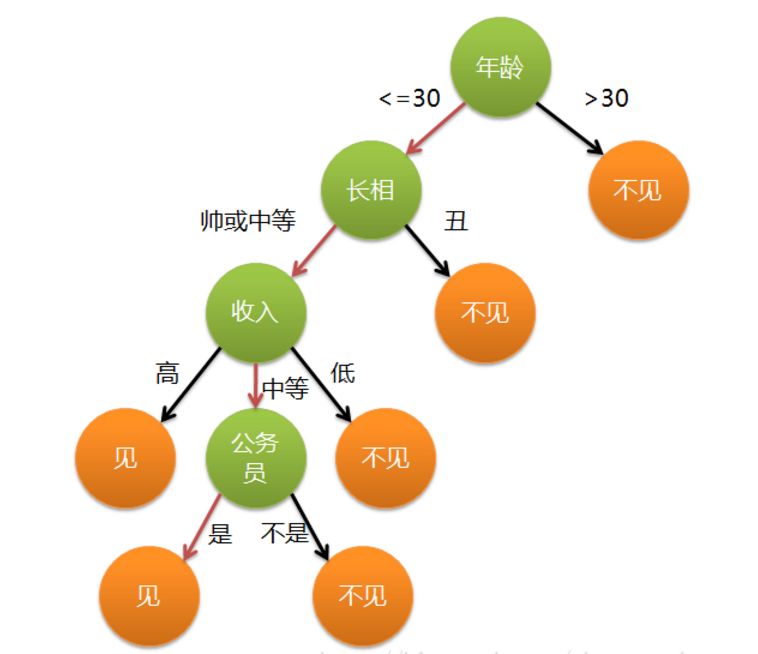
1. 决策树介绍

决策树基于树的结构进行决策，从根节点开始，沿着划分属性进行分支，直到叶节点：

• “内部结点”：有根结点和中间结点，某个属性上的测试（test），这里的test是针对属性进行判断
• “分支”：该测试的可能结果，属性有多少个取值，就有多少个分支
• “叶节点”：预测结果

1. 信息熵

“信息熵”(information entropy)是度量样本集合纯度最常用的一种指标。假定当前样本集合$D$中第$k$类样本所占的比例为$p_k(k=1,2,\dots ,|Y|)$，则$D$的信息熵定义为

$$Ent(D)=-{\sum }_{k=1}^{|y|}\frac{|D^v|}{D}Ent(D^v)$$
$$Ent(D^v)={\sum }_{v=1}^V{p}_{k}log{p}_k$$
$Ent(D)$的值越小，则 $D$的纯度越高。$Ent(D)$的最小值为0，最大值为$log{p}_k$

2. 信息增益

假定离散属性$a$有$V$个可能的取值$a1,a2,\dots ,aV$，若使用$a$来对样本集$D$进行划分，则会产生$V$个分支结点，其中第$v$个分支结点包含了$D$中所有在属性$a$上取值为$a^v$的样本，记为$D^v$。我们可根据式(1)计算出$D^v$的信息熵，再考虑到不同的分支结点所包含的样本数不同，给分支结点赋予权重$\frac{|D^v|}{|D|}$，即样本数越多的分支结点的影响越大，于是可计算出用属性a对样本集D进行划分所获得的"信息增益" (information gain)
$$Gain(D,a)=Ent(D)-{\sum }_{v=1}^V{p}_{k}log{p}_k$$
决策树学习应用信息增益划分属性。给定数据集$D$和属性$a$，信息熵$Ent(D)$表示对数据集$D$进行分类的不确定性。而$-{\sum }_{v=1}^{V}Ent(D^v)$ 是条件熵，表示在属性a给定的条件下对数据集$D$进行分类的不确定性。那么它们的差，即信息增益，就表示由于属性a而使得对数据集$D$的分类的不确定性减少的程度。显然，对于数据集$D$而言，信息增益依赖于特征，不同的特征往往具有不同的信息增益。

综上，信息增益越大，说明在知道属性 $a$ 的取值后样本集的不确定性减小的程度越大，也就是划分后所得的**“纯度提升”越大**。因此，我们可以根据信息增益进行划分属性的选择，方法是：对数据集（或子集）$D$，计算其每个属性的信息增益，并比较它们的大小，选择信息增益最大的特征。

3. 信息熵和信息增益

假设离散随机变量[公式]的概率分布为$P(Y)$，则其熵为

$H(Y)=-\sum P(y)logP(y)$ = $-\sum \frac{|C_k|}{|D|}log\frac{|C_k|}{|D|}$

其中熵满足不等式 $0\le H(Y)\le log|Y|$。
在进行特征选择时尽可能的选择在属性X确定的条件下，使得分裂后的子集的不确定性越小越好（各个子集的信息熵和最小），即$P(Y|X)$的条件熵最小

2. 使用sklearn实现决策树

1. 导入包和数据

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import csv
from sklearn.feature_extraction import DictVectorizer
from sklearn import preprocessing
from sklearn import tree

film_data = open('tree_data.csv','rt')
reader = csv.reader(film_data)

headers = next(reader)
# print(headers)

feature_list = [] # 特征值
result_list = [] # 结果（最后一列）

for row in reader:
    result_list.append(row[-1])

    # 去掉首位两列，特征集只保留'type','country' , 'gross'，将headers与row压缩成一个字典
    feature_list.append(dict(zip(headers[1:-1],row[1:-1])))
print(result_list)
print(feature_list)

2. 数据处理

vec = DictVectorizer() # 将 dict类型的list数据转换成 numpy array（特征向量化）
dummyX = vec.fit_transform(feature_list).toarray() # 做扁平化处理
dummyY = preprocessing.LabelBinarizer().fit_transform(result_list)
# print(dummyX)
# country  |  gnoss | type
# 0,0,0,0  | 0,0  | 0,0,0
# print(dummyY)

3. 开始训练模型

clf = tree.DecisionTreeClassifier(criterion='entropy',random_state=0)
clf = clf.fit(dummyX,dummyY)
print('clf=',str(clf))

4. 使用模型预测

##开始预测
A = ([[0,0,0,1,0,1,0,1,0]])#日本(4)-低票房(2)-动画片(3)
# B = ([[0，0，1，0，0，1，0，1，0]])#法国(4)-低票房(2)-动画片(3))
# C = ([[1，0，0，0，1，0， 1，0，0]]）#美国(4)-高票房(2)-动作片(3)
predict_result = clf.predict(A)

决策树可视化

import pydotplus
dot_data = tree.export_graphviz(clf,
                                feature_names=vec.get_feature_names(),
                                filled=True,
                                rounded=True, # 用圆角框
                                special_characters=True,
                                out_file=None)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf('film.pdf')

3. 附录

1. 关于 DictVectorizer( )

将 dict类型的list数据转换成 numpy array（特征向量化）。
DictVectorizer的处理对象是符号化(非数字化)的但是具有一定结构的特征数据，如字典等，将符号转成数字0/1表示。

dict_vec = DictVectorizer(sparse=False)# #sparse=False意思是不产生稀疏矩阵

#使用DictVectorizer对使用字典存储的数据进行特征抽取和向量化

#定义一组字典列表，用来表示多个数据样本（每个字典代表一个数据样本）
measurements = [{'city':'Beijing','temperature':33.},{'city':'London','temperature':12.},{'city':'San Fransisco','temperature':18.}]
#从sklearn.feature_extraction导入DictVectorizer
from sklearn.feature_extraction import DictVectorizer
vec = DictVectorizer()
#输出转化后的特征矩阵
print(vec.fit_transform(measurements).toarray())
#输出各个维度的特征含义
print(vec.get_feature_names())

# 输出：
#[[ 1.  0.  0. 33.]
# [ 0.  1.  0. 12.]
# [ 0.  0.  1. 18.]]
#['city=Beijing', 'city=London', 'city=San Fransisco', 'temperature']

2. 关于 dict(zip())

dict(zip()) 将两个列表合并成一个字典

假设你有如下两个list：

keys = ['name', 'age', 'food']
values = ['Monty', 42, 'spam']

如何转变成：

a_dict = {'name' : 'Monty', 'age' : 42, 'food' : 'spam'}

解决方法：

keys = ['a', 'b', 'c']
values = [1, 2, 3]
dictionary = dict(zip(keys, values))
print(dictionary)
# {'a': 1, 'b': 2, 'c': 3}

进阶，如果value是一个多级list呢：

keys= ['id', 'name', 'pwd']
values = [[2, '123', '567'],[3, '456', '899']]

解决方法：

keys= ['id', 'name', 'pwd']
values = [[2, '123', '567'],[3, '456', '899']]

# 先遍历rows里面的值，然后在用zip反转
a = [dict(zip(keys,values)) for row in values] if values else None
print(a)
# [{'name': [3, '456', '899'], 'id': [2, '123', '567']}, {'name': [3, '456', '899'], 'id': [2, '123', '567']}

3. 关于 tree.DecisionTreeClassifier

和其他分类器一样，DecisionTreeClassifier 需要两个数组作为输入：
X: 训练数据，稀疏或稠密矩阵，大小为 [n_samples, n_features]
Y: 类别标签，整型数组，大小为 [n_samples]

DecisionTreeClassifier() 模型方法中也包含非常多的参数值。例如：

• criterion = gini/entropy .可以用来选择用基尼指数或者熵来做损失函数。
• splitter = best/random .用来确定每个节点的分裂策略。支持 “最佳” 或者“随机”。
• max_depth = int 用来控制决策树的最大深度，防止模型出现过拟合。
• min_samples_leaf = int 用来设置叶节点上的最少样本数量，用于对树进行修剪。