基于Python的时间序列异常值检测

今天我们介绍几种常用的异常值检测方法，其中3sigma，z-score，箱体法(box)都是从数据值本身的单一维度去分析和判断异常值，从而有一定的局限性, 而多维度异常值判断法更注重从数据特征的各个维度去分析和判断异常值，显然多维度异常值判断法更为科学和精准。

-派神-

7032人浏览 · 2023-02-28 23:20:18

-派神- · 2023-02-28 23:20:18 发布

今天我们介绍一下使用python做时间序列数据分析和预测中异常值检测的方法，常用的异常值检测方法有以下几种：

3sigma: 基于正太分布，当数据值超过±3个标准差(3sigma)时为异常值。
z-score : z标准分数，它测量数据值到平均值的距离,当数据与平均值相差2个标准差时z-score为2，如果将z-score为3作为异常值判断标准时,便相当于3sigma。
箱体法(box): 它基于数据的四分位值来判断异常值。
多维度异常值判断法，通过数据特征的多个维度综合判断数据是否为异常值。

注：3sigma，z-score，箱体法(box)都是从数据值本身的单一维度去分析和判断异常值，从而有一定的局限性, 然而多维度异常值判断法更注重从数据特征的各个维度去分析和判断异常值，显然多维度异常值判断法更为科学和精准。

导入时间序列数据

我们的数据来自于某商业零售门店的每日客流量数据,客流量数据直接关系到门店销售业绩，所以有必要对客流量数据进行分析。

数据中的 y 列代表了客流量，这里数据的时间范围为2020.1至2023.1 ，接下来我们查看数据的趋势图。

plt.figure(figsize=(10,4),dpi=100)
plt.plot(df)
plt.title("客流量趋势")
plt.show()

下面我们查看客流量数据的热力图分布：

calplot.calplot(df.y,suptitle='客流量分布',cmap='YlGn');

从热力图的颜色深浅变化，我们也能发现客流量逐年在减少,这可能和疫情持续有关。

3sigma

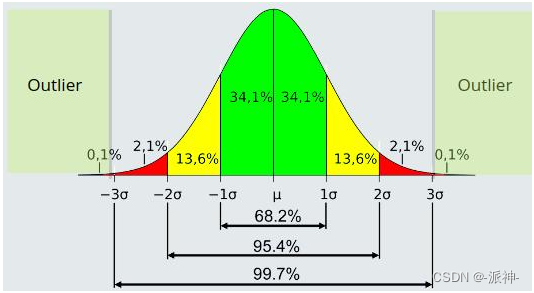
依据正太分布异常值分布在3个标准差以外的位置,如下图所示：

下面我们来计算数据的±3个标准以外的位置，落在这两个位置内的数据点即为异常值：

# 3sigma
def three_sigma(df):
    mean=df.y.mean()
    std=df.y.std()
    upper_limit=mean+3*std
    lower_limit=mean-3*std
    df['anomaly']=df.y.apply(lambda x: 1 if (x>upper_limit )
                              or (x<lower_limit) else 0)
    return df
df1 = three_sigma(df.copy())
df1[df1.anomaly==1]

fig, ax = plt.subplots(figsize=(10,4))
a = df1.loc[df1['anomaly'] == 1, ['y']] #anomaly
ax.plot(df.index, df['y'], color='blue', label='正常值')
ax.scatter(a.index,a['y'], color='red', label='异常值')
plt.title(f'3sigma')
plt.xlabel('date')
plt.ylabel('y')
plt.legend()
plt.show();

z-score

z-score测量数据值到平均值的距离,异常值的判断依据为给定的距离阈值，一般情况下阈值可以设置在大于2个标准差的任意位置(依据业务和经验来确定阈值)。如果将z-score为3作为异常值判定的阈值时,便相当于3sigma。

# Z-Score
def z_score(df,threshold):
    mean=df.y.mean()
    std=df.y.std()
    df['z_score']=df.y.apply(lambda x:abs(x-mean)/std)
    df['anomaly']=df.z_score.apply(lambda x: 1 if x>threshold else 0)
    return df

#设置阈值为2或3，当阈值为3时便相当于3sigma
threshold=2
df2 = z_score(df.copy(),threshold)
df2[df2.anomaly==1]

fig, ax = plt.subplots(figsize=(10,4))
a = df2.loc[df2['anomaly'] == 1, ['y']] 
ax.plot(df.index, df['y'], color='blue', label='正常值')
ax.scatter(a.index,a['y'], color='red', label='异常值')
plt.title(f'Z-score, {threshold=}')
plt.xlabel('date')
plt.ylabel('y')
plt.legend()
plt.show();

箱体法(box)

箱体法(box)基于数据的四分位值来判断异常值。异常值>Q3+1.5*IQR 或者异常值<Q1-1.5*IQR

def box_plot(df):
    q1=np.nanpercentile(df.y,25)
    q3=np.nanpercentile(df.y,75)
    iqr=q3-q1
    lower_limit=q1-1.5*iqr
    upper_limit=q3+1.5*iqr
    df['anomaly']=df.y.apply(lambda x: 1 if x<lower_limit or x>upper_limit  
                             else 0)
    return df
df3 = box_plot(df.copy())
df3[df3.anomaly==1]

fig, ax = plt.subplots(figsize=(10,4))
a = df3.loc[df3['anomaly'] == 1, ['y']] 
ax.plot(df.index, df['y'], color='blue', label='正常值')
ax.scatter(a.index,a['y'], color='red', label='异常值')
plt.title(f'Box-plot')
plt.xlabel('date')
plt.ylabel('y')
plt.legend()
plt.show();

多维度异常检测法PyOD

异常检测算法工具库(PyOD) 可以从数据的多个特征维度来检测异常值，所以我们可以将时间序列数据的日期特征分解成多个和时间相关的其它特征,同时我们还需要设置一个异常值比例,一般情况下我们设置异常值比例在5%以下。这里我们使用的是Pycaret的异常值检测模型,该模型是对PyOD进行了再次包装,使之调用更为简单，感兴趣的朋友可以去查看Pycaret和PyOD的相关文档。这里我们首先将日期字段进行分解，从原始的日期字段中我们可以拆分出年，月，日，星期，季度等和时间相关的特征：

from pycaret.anomaly import AnomalyExperiment
# 分解日期特征
def create_features(df):        
    df['year'] = df.index.year #年 
    df['month'] = df.index.month #月
    df['dayofmonth'] = df.index.day #日
    df['dayofweek'] = df.index.dayofweek #星期
    df['quarter'] = df.index.quarter #季度
    df['weekend'] = df.dayofweek.apply(lambda x: 1 if x > 5 else 0) #是否周末
    df['dayofyear'] = df.index.dayofyear   #年中第几天
    df['weekofyear'] = df.index.weekofyear #年中第几月
    df['is_month_start']=df.index.is_month_start
    df['is_month_end']=df.index.is_month_end
    return df
#创建特征
df4 = create_features(df.copy())
df4

接下来我们使用Pycaret的anomaly模型对新数据集进行建模和预测，同时我们仍然需要设置一个异常值比例的阈值fraction：

#异常值算法：'knn','cluster','iforest','svm'等。
alg='knn'#异常值算法
fraction=0.02 #异常值比例 0.02,0.03,0.04,0.05
#创建异常值模型
exp = AnomalyExperiment()
r = exp.setup(df4.copy(), session_id = 123,verbose=False)
model = exp.create_model(alg, fraction=fraction,verbose=False)
model_results = exp.assign_model(model,verbose=False)
#获取检测结果
df5 = pd.merge(df.reset_index(),model_results[['Anomaly']],
               left_index=True, right_index=True)
df5.set_index('date',inplace=True)

fig, ax = plt.subplots(figsize=(10,4))
a = df5.loc[df5['Anomaly'] == 1, ['y']] 
ax.plot(df5.index, df5['y'], color='blue', label='正常值')
ax.scatter(a.index,a['y'], color='red', label='异常值')
plt.title(f'Pycaret.anomaly {fraction=}')
plt.xlabel('date')
plt.ylabel('y')
plt.legend()
plt.show();