上一篇：深入浅出NandFlash里的ECC校验算法原理与实现(1)

距离笔者写上篇关于ECC校验已经过去7个月，本来是不打算填坑的，但是看上篇还是有一些人收藏的，鉴于此，打算把ECC校验源码实现解析补全。看了很多篇解析，大部分出自同一篇。但是笔者认为都没有把原理完完全全写清楚。这篇文章也是想了很久才下笔，希望把源码中的原理与思路彻底讲透，个人认为，把一个东西原理讲清楚相对比较简单，但是想把思路讲清楚，很难很难。

LINUX-2.6.27中ECC校验源码：

LXR linux/drivers/mtd/nand/nand_ecc.c

笔者不打算从源码开始讲，而是想从为什么这么做开始。

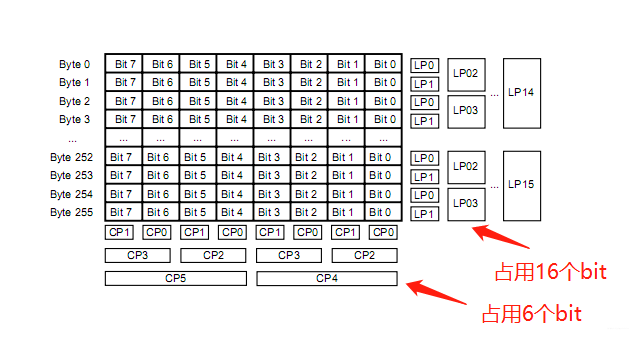
1.计算CP0~CP5

这张图取自上一篇博文，可以看到，256个byte，每个都为一个uint8类型的数字，假如现在让你计算CP0~CP5你会怎么计算呢？如果是我，首先想到的肯定是for循环，比如：

unsigned char data[256] = {0};//存储着待计算的数据
unsigned char CP0,CP1,CP2,CP3,CP4,CP5,res;
for(int i=0;i<256;i++)
{
    CP0 ^= (data[i]>>0)^(data[i]>>2)^(data[i]>>4)^(data[i]>>6);
    CP1 ^= (data[i]>>1)^(data[i]>>3)^(data[i]>>5)^(data[i]>>7);
    CP2 ^= (data[i]>>0)^(data[i]>>1)^(data[i]>>4)^(data[i]>>5);
    CP3 ^= (data[i]>>2)^(data[i]>>3)^(data[i]>>6)^(data[i]>>7);
    CP4 ^= (data[i]>>0)^(data[i]>>1)^(data[i]>>2)^(data[i]>>3);
    CP5 ^= (data[i]>>4)^(data[i]>>5)^(data[i]>>6)^(data[i]>>7);
}
res = 0x03|((CP0&0x01)<<2)|((CP1&0x01)<<3)|((CP2&0x01)<<4)|((CP3&0x01)<<5)|((CP4&0x01)<<6)|((CP5&0x01)<<7);

这里我把每个数据取出来计算它们的CP0~CP5，用for循环把计算结果与下一个数据的计算结果相异或。有些人可能延续上一章的思路，想先计算256个数据的bit0异或结果，再分别计算256个数据的bit2、bit4、bit6结果，最后把这个四个结果再异或得到CP0，但是这样岂不是需要4个for循环？这样是先计算每列的异或，其实如果先计算每行的异或是一模一样的。比如我先计算第0个字节的bit0、bit2、bit4、bit6异或结果，再依次计算所有数据的，最终把它们都异或，结果是一样的。

如果直接把for循环里面的CP0~CP5带入到res中，可以得到更加简化的：

for(int i=0;i<256;i++)
{
    res ^=                                                             \
    (((data[i]>>0)^(data[i]>>2)^(data[i]>>4)^(data[i]>>6))&0x01)<<2|   \
    (((data[i]>>1)^(data[i]>>3)^(data[i]>>5)^(data[i]>>7))&0x01)<<3|   \
    (((data[i]>>0)^(data[i]>>1)^(data[i]>>4)^(data[i]>>5))&0x01)<<4|   \
    (((data[i]>>2)^(data[i]>>3)^(data[i]>>6)^(data[i]>>7))&0x01)<<5|   \
    (((data[i]>>0)^(data[i]>>1)^(data[i]>>2)^(data[i]>>3))&0x01)<<6|   \
    (((data[i]>>4)^(data[i]>>5)^(data[i]>>6)^(data[i]>>7))&0x01)<<7;   
}
res |=0x03;

到这里，你应该很容易明白空间和时间的转换，如果我们把uint8所能表示的数的CP0~CP5全部先计算好保存起来，然后在实际计算中不再去计算每个data的CP0~CP5，可以大大加快代码运行时间，这就是用空间增大换取时间减小。可是具体怎么操作呢？

我们知道uint8类型所能表示的数是0~255，如果数据是129，怎么用最快的方法找到129计算好的CP0~CP5？

答案是·按顺序存储，第0个就存0的CP0~CP5，第129就存129的CP0~CP5，这样把所有结果都存好就形成了一个数组假设叫做nand_ecc_precalc_table[256] ，假如求129的CP0~CP5，直接取

nand_ecc_precalc_table[129]的值即可！

现在我们再去看linux内核中的代码：

需要说明的是，nand_ecc_precalc_table 这个数组里，每个元素的bit0~bit5分别对应等于索引的CP0~CP5，有细心的朋友会发现其实并不一定相等！因为它还多储存了一位bit6，它代表这个数据的所有位异或的结果，比如129的二进制是 1000 0001，所以所有位异或结果是0，那nand_ecc_precalc_table[129]的bit6保存就是0。所以你可以看到，在取到数据索引相对应的数据后，先做了 &0x3F ，即取前6位，而bit6在下面计算行校验中才会被用到。

2.计算LP0~LP15

linux内核中用来计算行校验的方法很巧妙，笔者一开始也没有看懂，如果让你去写一段代码去计算行校验，你会怎么写？

由上一节计算列校验的思路，我们有256个数据，即256行，每一行所有位异或结果保存在1个bit中，256个bit即32个字节，然后我们将用一段庞大的for循环代码去计算LP0~LP15,比如：

unsigned char lData[32];//储存所有列异或计算结果
unsigned char LP0,LP1,LP2,LP3,tmp;
for(int i=0;i<32;i++)
{
    tmp ^= data[i];
}
LP0 = ((tmp>>0)^(tmp>>2)^(tmp>>4)^(tmp>>6))&0x01;
LP1 = ((tmp>>1)^(tmp>>3)^(tmp>>5)^(tmp>>7))&0x01;
LP2 = ((tmp>>0)^(tmp>>1)^(tmp>>4)^(tmp>>5))&0x01;
LP3 = ((tmp>>2)^(tmp>>3)^(tmp>>6)^(tmp>>7))&0x01;
...

你会发现当计算到LP6、LP7的时候，需要再用一个for循环,而到LP8、LP9的时候可能还需要一个循环，当然有些循环也可以合并，但是不可否认的是代码量和计算都需要很多。有没有更简单的办法？

现在到本文中最精彩的地方。

（2022-12-17注：后来再看这篇文章，感觉有些地方还可以讲的更清楚，所以又已一种更为清晰的思路讲了一遍，第一次看的可以先看后面的）

第一个问题，LP0到底求的是什么？

图1很重要， 我需要再放一张图1：

由图1我们不难看出LP0所求的是所有偶数行异或结果！

第二个问题，异或结果是什么？

很简单，每个偶数行的计算结果要么是0，要么是1，如果偶数行的计算结果为1的行最后有奇数个，则LP0=1，如果为偶数个则LP0=0！异或运算说简单点就是消消乐，相同就可以消掉=0，不相同就消不掉=1，偶数个都能配对上消掉，奇数个总有一个配不上对儿咯。

第三个问题，怎么判断是偶数行还是奇数行？

很简单，用数学方法就是除以2，如果有余数则为奇数，没有余数则为偶数。但是怎么用程序员的方法判断呢？

判断行号的bit0，如果bit0=0则为偶数行，如果bit0=1则为奇数行！

第四个问题，判断偶数行号的计算为1的行是有偶数个还是有奇数个怎么做？

最简单的思路是把计算结果为1的行数累加，最后结果除以2判断是奇数还是偶数，最后就得到LP0=1还是=0，但是如果我们直接把累加换成异或呢？

假如所有偶数行中有7个行计算结果为1，剩下121个偶数行都是0，如果我们累加，则累加结果sum=7，sum/2=3余1，所以有奇数个，所以LP0=1，但是如果我们申请一个变量LP，每次判断计算结果，如果为1，不累加，而是令LP ^= 1 ，如果为0，则什么也不做。经过7次后，LP=1！也就是我们用异或的方法去计算计算结果为1的偶数行是有奇数个还是有偶数个！ 

到这里我们捋一下思路，按照我们的问题，假如我们是求LP0，即：

1求LP0 -> 

2求所有属于LP0的行的异或结果 ->

3属于LP0的行的行号都是偶数，所以是求所有偶数行异或结果 -> 

4我们把行号除以2根据余数判断是不是偶数行 ->

5判断出来是偶数行，则把这一行的异或结果(即上文的bit6)累加 ->

6最后把累加结果除以2，判断偶数行是有奇数个还是偶数个

但是根据我们上面讲到的判断奇偶行和最终有奇数个还是偶数个偶数行个数的方法，可以变为：

1求LP0 -> 

2求所有属于LP0的行的异或结果 ->

3属于LP0的行的行号都是偶数，所以是求所有偶数行异或结果 -> 

4我们根据行号的bit0判断是不是偶数行 ->

5判断出来是偶数行，则把这一行的异或结果与上一次异或结果异或，最终异或结果为1则为奇数个，为0则为偶数个

我们知道了关于LP0的这么多又有什么用呢？不能每个LP都判断一遍吧？那感觉还不如传统思路！

如果把上面四个思路都集合到一起：

uint8_t lData[256];//每个行最终的计算结果，不为0，即为1
uint8_t LP0;
for(uint8_t i=0;i<256;i++)
{
    if(lData[i])//如果行最终计算结果为1
    {
        LP0 ^= ~(i&0x01);
    }
}
LP0 &= 0x01;//只取bit0

这其中最重要的一点：偶数行必定bit0为0，则取反必定为1(问题3)。如果每次判断行的计算结果为1，则计数一次，计数的方法就是上面的问题四：异或1，而这个1就是行号bit0取反得到的1！由此，我们通过判断bit0的最终结果为0还是为1来判断有奇数个还是偶数个。

同理，我们求LP1可以：

uint8_t lData[256];//每个行最终的计算结果，不为0，即为1
uint8_t LP1;
for(uint8_t i=0;i<256;i++)
{
    if(lData[i])//如果行最终计算结果为1
    {
        LP1 ^= (i&0x01);
    }
}
LP1 &= 0x01;//只取bit0

因为奇数行的bit0必定为1，所以碰到计算结果为1的，直接异或行号的bit0即可计数！

我们继续往下推，LP2和LP3、LP4和LP5等等怎么计算？我们如何从LP0和LP1的判断奇偶数行推广到LP2~LP15？

这牵扯到一个问题，第五个问题，给你一个行号，怎么判断它属于哪些LP？这个问题是把从LP0~LP1推广到LP2~LP15的关键！

举个例子，行号120属于哪些LP？

LP0和LP1很容易判断，数学原理是除以2看是否有余数，无余数为LP0，有余数为LP1，而我们用程序员的办法就是判断bit0，bit0是0为偶数，bit0是1为奇数。

LP2和LP3我们总结一下：

属于LP2的行：0、1、4、5、8、9、12、13......252、253

属于LP3的行：2、3、6、7、10、11、14、15......254、255

同时再由 图1 去观察，很容易发现，LP2和LP3是2个元素为1组，所以我们可以发现上述规律稍微总结一下：

属于LP2的行：【0、1】、【4、5】、【8、9】、【12、13】......【252、253】

属于LP3的行：【2、3】、【6、7】、【10、11】、【14、15】......【254、255】

如果把临近的元素看做一组，则256个结果可以分为128个组，偶数组为LP2，奇数组为LP3！

也就是上面的【0、1】为组号0，【2、3】为组号1，一直这么分下去。怎么由这个规律求得行号120是属于LP2还是LP3？

很简单，120÷2=60，它被分在组号60第0个，也就是偶数组，也就是LP2！你可以试一下，如果行号是7,7÷2=3余1，它被分在组号3第1个，也就是奇数组，它属于LP3！所以不看余数，只看结果是偶数还是奇数，即可判断是LP2还是LP3！

发散一下思维，再次使用程序员的办法，把除法转换为移位，除以2相当于右移1位，然后我们判断右移后的bit0，如果是0则为偶数组，如果为1则为奇数组！从而判断属于LP2还是LP3！

再次发散思维，对应LP4和LP5，我们以4个临近元素为1组，同样的，偶数组属于LP4，奇数组属于LP5，我们的数学办法是除以4，看结果，转换一下，右移两位，看bit0，如果bit0为0则为LP4，如果bit0为1则为LP5！

接下来推广到所有情况，最终的LP14和LP15是以128个临近元素为1组，右移7位，bit0为0则属于LP14，否则为LP15！

同样的，在判断完奇偶组后，就像LP0和LP1那样，直接以bit0异或，即可得出结果，既然每次分组位移的位数不同，我们直接异或，不同位之间并不影响，也不再需要右移，而是取位的时候直接取对应位即可！

即行号的每个bit有：

bit0=0，属于LP0，bit0=1，属于LP1，每当有属于LP0的数据计算结果为1时，计数！即reg2 ^= 1，每当有属于LP1的数据计算结果为1时，计数！即reg3 ^=1，这个1刚好被替换为bit0，可是当属于LP0的时候bit0是0啊？那就取反！最终LP0计数时reg2 ^= ~bit0，LP1计数时reg3 ^=bit0。

同理bit1=0，属于LP2，bit1=1，属于LP3，每当有属于LP2的数据计算结果为1时，也计数，我们不再用bit0计数，而是用bit1计数，这样刚好能和上面的情况分开，且计数方式统一！，即LP2计数时reg2 ^= ~bit1，LP3计数时reg3 ^= bit1，最终，我们通过判断reg2的bit1来判断属于LP2的行中，计算结果为1的行总数为奇数个还是偶数个，通过判断reg3的bit1来判断属于LP3的行中，计算结果为1的行总数为奇数个还是偶数个，从而得到LP2和LP3到底等于0还是等于1！

后面的不再赘述：

bit2=0，属于LP4，bit2=1，属于LP5

bit3=0，属于LP6，bit3=1，属于LP7

bit4=0，属于LP8，bit4=1，属于LP9

bit5=0，属于LP10，bit5=1，属于LP11

bit6=0，属于LP12，bit6=1，属于LP13

bit7=0，属于LP14，bit7=1，属于LP15

最终我们得到一下代码：

uint8_t lData[256];//每个行最终的计算结果，不为0，即为1
uint8_t reg2,reg3,LP0,LP1,LP2,LP3,LP4,LP5,LP6,LP7,LP8,LP9,LP10,LP11,LP12,LP13,LP14,LP15;
for(uint8_t i=0;i<256;i++)
{
    if(lData[i])//如果行最终计算结果为1
    {
        reg2 ^= ~i;
        reg3 ^= i;
    }
}
//每个位之间并不影响结果，最终可以拆分为以下结果
LP0 = reg2 & (1<<0);
LP1 = reg3 & (1<<0);
LP2 = reg2 & (1<<1);
LP3 = reg3 & (1<<1);
LP4 = reg2 & (1<<2);
LP5 = reg3 & (1<<2);
LP6 = reg2 & (1<<3);
LP7 = reg3 & (1<<3);
LP8 = reg2 & (1<<4);
LP9 = reg3 & (1<<4);
LP10 = reg2 & (1<<5);
LP11 = reg3 & (1<<5);
LP12 = reg2 & (1<<6);
LP13 = reg3 & (1<<6);
LP14 = reg2 & (1<<7);
LP15 = reg3 & (1<<7);

上图为了让大家明白对应关系，把reg2和reg3拆分了一下，实际代码中直接把reg2和reg3的每一位取出来，位移到最终生成的那3个字节的结果上对应的位即可！

贴一下linux内核中的代码：

 这里的 &0x40 即取第6位，上文中提到过第六位存储的是数据所有位异或结果。

总结

计算CP就用传统思路，只不过先把所有数结果计算好，实际直接查表，不再需要运行时计算。

计算LP为0还是为1 <==> 计算属于这个LP的数据所有位异或结果为1的有奇数个还是偶数个 <==> 判断每个数据都属于哪些LP，当这个数据所有位异或结果为1时，它所属的那些LP统统计数1次 <==> 判断每个LP最后的计数结果得到对应LP为1还是为0

更新 2022.12.16：

我又回头看了一下当时写的这篇文章，突然感觉还是没有抓到精髓，虽然当时我已经把ECC校验算法搞懂了，但是描述行校验的时候却用了一种复杂的方法。现在我重新用一种更为通俗易懂的方式再讲一下。

还是这张图， 根据我前面的分析：

1.每一个byte的8个bit构成一行，把这8个bit异或，最后得到1位，我们可以称为这一行的异或结果，占1bit。byte0，我们可以叫做第0行，byte1是第一行，等等，后续同理。

2.然后我们需要知道一个行属于哪些LP！

为什么要得到一个行属于哪些LP呢？因为我们只要知道了一个行属于哪些LP，那我们把所有行都循环1次，每次判断它属于哪些LP，然后，把这个行的异或结果与对应的LP异或就可以了。逻辑是这样的：

假如256个字节，即256行，每行异或结果放在data[256]里，则有：

初始化：LP0=LP1=LP2=LP3=LP4=LP5=LP6=LP7=LP8=LP9=LP10=LP11=LP12=LP13=LP14=LP15=0;

然后循环判断：

for(int i=0;i<256;i++)

{

    if(第i行属于LP0)

    {

        LP0 = LP0 ^ data[i];

    }    

    if(第i行属于LP1)

    {

        LP1 = LP1 ^ data[i];

    }    

    if(第i行属于LP2)

    {

        LP2 = LP2 ^ data[i];

    }    

......等等，不再赘述

    if(第i行属于LP15)

    {

        LP15 = LP15 ^ data[i];

    }    

}

从上面可以看出来，256个byte只要循环256次，每次判断16次，就可以算出来LP0~15。我们找出每一行属于哪些LP，然后列举一部分：

第0行属于：LP0/LP2/LP4/LP6/LP8/LP10/LP12/LP14

第1行属于：LP1/LP2/LP4/LP6/LP8/LP10/LP12/LP14

第2行属于：LP0/LP3/LP4/LP6/LP8/LP10/LP12/LP14

第3行属于：LP1/LP3/LP4/LP6/LP8/LP10/LP12/LP14

......

第255行属于：LP1/LP3/LP5/LP7/LP9/LP11/LP13/LP15

请思考，如果给你一个行号，比如117，你知道它都属于哪些LP吗？

可以先自己尝试思考一下再看下面的思路。

3.由上面的图，我们可以很容易看出来，计算LP0就是异或所有偶数行的值。同理计算LP1就是异或所有奇数行的值，最终结果都是1bit。我们可以再看图，或者用最笨的办法，一个个数，列举每个LP都有哪些行，比如：

LP0包含：第0行、第2行、第4行......第254行。(从第0行开始，每1行看作一个组，可以分为256个组，偶数组)

LP1包含：第1行、第3行、第5行......第255行。(从第0行开始，每1行看作一个组，可以分为256个组，奇数组)

LP2包含：第0行、第1行、第4行、第5行......第252行、第253行。(从第0行开始，每相邻的2行看作一个组，可以分为128个组，偶数组，组是这样划分的：第0、1行是第0组，第2、3行是第1组，下面同理)

LP3包含：第2行、第3行、第6行、第7行......第254行、第255行。(从第0行开始，每相邻的2行看作一个组，可以分为128个组，奇数组)

......

......

LP14包含：第0行、第1行、第2行......第127行。(从第0行开始，每相邻的128行看作一个组，可以分为2个组，偶数组)

LP15包含：第128行、第129行、第130行......第255行。(从第0行开始，每相邻的128行看作一个组，可以分为2个组，奇数组)

所以判断一个行属于LP0还是LP1，我们可以判断它是奇数行还是偶数行，就拿上文说的行号117来说，117/2=58余1，所以是奇数行，所以117属于LP1！

但是其实看二进制的数字，很容易看出来，117是0111 0101，它的最低位是1，肯定是一个奇数！

那判断它属于L2还是LP3呢？我们把2个相邻的行看作一组，117/2=58余1，所以它是第58组的第1个，它是偶数组，所以它属于LP2，看到这你也应该发现了，二进制的117的bit1=0，所以它除以2（就相当于右移1位）的结果是偶数，我们这里不关心余数，只看结果。

同理，判断117属于LP4还是LP5，可以让117/4=29余1，相当于4个行划分为1组的情况下，它属于奇数组，所以它属于LP5，同样的除以4相当于右移2位，我们其实看的就是bit2！bit2=1，所以除以4后是奇数！

中间情况不再赘述。

最后，对于LP14还是LP15，我们是按128个行划分为一组，所以117/128=0余117，所以是偶数组，看的其实就是bit7！

所以我们判断117（0111 0101）属于哪些LP，其实看的就是它的bit0~bit7:

bit0=1，属于LP0~1中的LP1

bit1=0，属于LP2~3中的LP2

bit2=1，属于LP4~5中的LP5

...

bit6=1，属于LP12~13中的LP13

bit7=0，属于LP14~15中的LP14

所以，我们之前的代码逻辑可以改为：

for(int i=0;i<256;i++)
{
    if(i&(0x01<<0))//判断属于LP0还是1
    {
        LP1 = LP1 ^ data[i];//第0位是1
    } 
    else
    {
        LP0 = LP0 ^ data[i];//第0位是0
    }  
    if(i&(0x01<<1))//判断属于LP2还是3
    {
        LP3 = LP3 ^ data[i];//第1位是1
    }    
    else
    {
        LP2 = LP2 ^ data[i];//第1位是0
    }  

......等等，不再赘述

    if(i&(0x01<<7))//判断属于LP14还是15
    {
        LP15 = LP15 ^ data[i];//第7位是1
    }    
    else
    {
        LP14 = LP14 ^ data[i];//第7位是0
    }  
}

我们可以再一步简化这个代码！这里大概就是整个ECC代码最精妙的地方了。

异或运算的法则是：

0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0

这是否意味着，当data[i]=0时，其实我们是不用异或的，因为0异或后还是原来的值。

所以我们可以简化一下，比如LP0和LP1的计算：

for(int i=0;i<256;i++)
{
    if(data[i])
    {
        if(i&(0x01<<0))//判断属于LP0还是1
        {
            LP1 = LP1 ^ data[i];//第0位是1
        } 
        else
        {
            LP0 = LP0 ^ data[i];//第0位是0
        }  

......等等，不再赘述

        if(i&(0x01<<7))//判断属于LP14还是15
        {
            LP15 = LP15 ^ data[i];//第7位是1
        }    
        else
        {
            LP14 = LP14 ^ data[i];//第7位是0
        }  
    }
}

也就是这一行的计算结果为1时，我们再去判断它属于哪些LP！

那我们再简化一下：

for(int i=0;i<256;i++)
{
    if(data[i])
    {
        if(i&(0x01<<0))//判断属于LP0还是1
        {
            LP1 = LP1 ^ 1;//第0位是1
        } 
        else
        {
            LP0 = LP0 ^ 1;//第0位是0
        }  
    }
}

既然只有data[i]=1才计算，那我直接在满足条件的情况下把data[i]替换成1，这很合理吧。

再进一步简化，既然LP1 = LP1 ^ 1这个运算只有在i的bit0为1的时候才满足，那我把1替换成i的bit0是否更加简单？

for(int i=0;i<256;i++)
{
    if(data[i])
    {
        if(i&(0x01<<0))//判断属于LP0还是1
        {
            LP1 = LP1 ^ (i&(0x01<<0));//第0位是1
        } 
        else
        {
            LP0 = LP0 ^ (~(i&(0x01<<0)));//第0位是0
        }  
    }
}

上面代码中，我甚至直接把i的bit0等于0时，LP0异或的1替换成了i的bit0取反，因为它必为0，取反必为1。

看一下上面的代码逻辑，如果i的bit0等于1，则LP1异或1。那如果是0的话我让它异或0，对结果也没有影响！那干嘛还判断呢？所以我们再简化：

for(int i=0;i<256;i++)
{
    if(data[i])
    {
        LP1 = LP1 ^ (i&(0x01<<0));//第0位是1
        LP0 = LP0 ^ (~(i&(0x01<<0)));//第0位是0
    }
}

 同时我们把所有情况补全：

for(int i=0;i<256;i++)
{
    if(data[i])
    {
        LP1 = LP1 ^ (i&(0x01<<0));//第0位是1
        LP0 = LP0 ^ (~(i&(0x01<<0)));//第0位是0
        LP3 = LP3 ^ (i&(0x01<<1));//第1位是1
        LP2 = LP2 ^ (~(i&(0x01<<1)));//第1位是0
        LP5 = LP5 ^ (i&(0x01<<2));//第2位是1
        LP4 = LP4 ^ (~(i&(0x01<<2)));//第2位是0
        LP7 = LP7 ^ (i&(0x01<<3));//第3位是1
        LP6 = LP6 ^ (~(i&(0x01<<3)));//第3位是0
        LP9 = LP9 ^ (i&(0x01<<4));//第4位是1
        LP8 = LP8 ^ (~(i&(0x01<<4)));//第4位是0
        LP11 = LP11 ^ (i&(0x01<<5));//第5位是1
        LP10 = LP10 ^ (~(i&(0x01<<5)));//第5位是0
        LP13 = LP13 ^ (i&(0x01<<6));//第6位是1
        LP12 = LP12 ^ (~(i&(0x01<<6)));//第6位是0
        LP15 = LP15 ^ (i&(0x01<<7));//第7位是1
        LP14 = LP14 ^ (~(i&(0x01<<7)));//第7位是0
    }
}

可以看到，每个位都不相同，所以他们互不影响，我们做最后一次简化：

for(int i=0;i<256;i++)
{
    if(data[i])
    {
        reg1 ^= i;
        reg2 ^= ~i;
    }
}

其中reg1的bit0=LP1，bit1=LP3......bit7=LP15

reg2的bit0=LP0，bit1=LP2......bit7=LP14

至此，与Linux内核中的代码就一模一样了。

更新2023-06-25：

有朋友对源码中的 nand_correct_data 函数不太理解，我看了一下，确实，如何生成ECC我已经剖析过了，但是如何还原数据还没有讲过，这个函数就是如何通过计算还原数据，这里补充一下。

我这里只分析CP0-5的情况，LP0-LP15同理。

首先我们假设数据在存储过程中，出现的错误是byte132的bit2发生了翻转。这会导致什么？仔细看过我前面分析的朋友应该很快可以回答：

这会导致CP0、CP3、CP4的计算结果发生翻转。

这里容我再再再放一次这两张很重要的图：

由上图可以很明显看出来，bit2发生翻转会导致它所属于的CP最终的计算结果都发生翻转。假如ECC三个字节分别是S0、S1、S2，我们只讨论CP0~5，所以只看S2，这里假设Nand里面存的S2的二进制是0100 1111(最低两位固定为1)，而现在我们已经知道了是bit2发生了翻转，那我们实际计算得到的S2应该是0010 1011。

所以，我们现在的问题就是，假如Nand里存储的S2是0100 1111，我们根据Nand里存的数据实际计算得到的S2是0010 1011，怎么通过计算得到是bit几发生了翻转？(感觉有点废话，但确实反推更容易理解)

很简单，我们只需要把两个结果一异或，就可以看出来是哪些bit发生了变化，比如这里0100 1111^0010 1011 = 01100100，由这个结果对比上图的表格，就可以知道是CP0、CP3、CP4发生了变化。正常的思路接下来当然是判断都有哪些bit是1，然后就可以确定是哪个bit发生了翻转。比如：

if(bit2&&bit5&&bit6)

{

  bit2发生了翻转

}

这种思路最坏情况需要把bit0~bit7所有bit翻转的情况都判断一遍，这样会有8个if/else if来判断0~7bit哪个bit发生了翻转。为了追求极致的运行速度，内核中使用了更精妙的办法。

其实这个办法和我上面讲的判断当前行属于哪些LP一样的原理。

bit0二进制是000，属于CP0、CP2、CP4

bit1二进制是001，属于CP1、CP2、CP4

bit2二进制是010，属于CP0、CP3、CP4

bit3二进制是011，属于CP1、CP3、CP4

bit4二进制是100，属于CP0、CP2、CP5

bit5二进制是101，属于CP1、CP2、CP5

bit6二进制是110，属于CP0、CP3、CP5

bit7二进制是111，属于CP1、CP3、CP5

这里你应该能看出来两条规律：

1.CP0和CP1、CP2和CP3、CP4和CP5是互斥的，也就是属于其中一个就一定不属于另一个

2.属于哪个CP，可以间接得到对应bit应该是1还是0，比如属于CP5，那bit号的第三个bit一定为1

所以，由上面我们举的例子：

0100 1111 ^ 0010 1011 = 01100100

因为互斥规则，我们只需判断1、3、5或者0、2、4，这里我们选择判断1、3、5。取Nand存的S2是S2_1，我们计算得到的S2是S2_2，判断如下：

u8 bit = 0;

u8 S22 = (S2_1^S2_2);//S22=01100100

if(S22&(1<<7))

bit |= 1<<2;

if(S22&(1<<5))

bit |= 1<<1;

if(S22&(1<<3))

bit |= 1<<0;

上述代码最终求得的bit = 2，表示是bit2发生了翻转。对于内核来说，这还是太慢了，根据我之前讲的如何求reg2和reg3的简化方法，我们可以把或上的位直接转化为判断条件中的位，所以上述代码可以精简为：

bit |=((S22>>7)<<2)&(1<<2);

bit |=((S22>>5)<<1)&(1<<1);

bit |=((S22>>3)<<0)&(1<<0);

把多余的表达删掉，最终代码是：

bit |=(S22>>5)&(0x04);

bit |=(S22>>4)&(0x02);

bit |=(S22>>3)&(0x01);

如果没有初始化bit = 0，可以把第一个或等于改成直等。

还有这里有做几个判断，都是跳过某些情况的，我主要讲一下下面的判断：

我在第一篇开篇就讲过，文章中的ECC校验只能修复一个bit发生翻转的情况，当翻转了多个bit，那么就无法应对了，所以需要对这种情况进行判断。

那么该如何判断呢？

首先这一步计算得到的s2的含义上文已经说过，哪个bit置1，表示哪个CP发生了数据翻转，比如之前举的例子0110 0100，表示CP0、CP3、CP4发生了翻转。

数据	bit7	bit6	bit5	bit4	bit3	bit2	bit1	bit0
s2	CP5	CP4	CP3	CP2	CP1	CP0	0	0
s2>>1	0	CP5	CP4	CP3	CP2	CP1	CP0	0
异或后的值	0或1	1	0或1	1	0或1	1	0或1	0
0x54	0	1	0	1	0	1	0	0

 这里需要注意，CP0和CP1、CP2和CP3、CP4和CP5可能同时为0或者同时为1吗？

答案是当只有一个原始数据的一个位发生翻转时，它们不可能同时发生翻转，因为一个位不可能既属于CP0又属于CP1或者既不属于CP0又不属于CP1。所以从上表也可以看出来，异或后的值 “与” 上0x54后，必定等于0x54，除非本该互斥的那些CP同时等于0或者等于1，此时，证明不止有一个bit发生了翻转！

遗留思考：分析LP如何还原，另外假如有很多bit都发生了翻转，此函数可以应对吗？