在之前的内容中谈到。为避免PI调节器参数调节困难的问题、PI调节器动态性能不足的问题，我们采用了无差拍预测电流控制（DPCC）。但是DPCC是属于模型预测控制（MPC）中的一种，需要精确的电机参数，但出现参数失配时，系统的性能就会大打折扣。

        为提高DPCC的鲁棒性，上一小节我们引入了ESO，有效提高了系统的参数鲁棒性。但其实可以发现，在DPCC的基础上，引入了ESO，增加了系统的复杂度，而且还需要系统参数。假如我们的观测器ESO，设置的非常好，性能非常nice，那岂不是不需要电机参数吗？确实是这样的。所以我们在这一文中，将介绍，基于ESO的永磁同步电机无模型预测电流控制（Model-Free Predictive Current Control/MFC）。

参考文献：

论文来源：TIE（TOP期刊）

论文作者：国内做预测控制的大佬。（如果大家对电机的预测控制感兴趣，可以多看看张老师的文章）

传统的MFC模型：

        u就是系统的输入，刚好就是电机的电压；y就是电机的电流。F为系统的未知扰动（这是需要我们进行估计的）。α为需要调节的参数（过大的话，系统振荡，不稳定）。在式（5）中可以看到，传统的MFC还需要整定参数Kp。而且F的估计也是比较复杂的（文章里面没说，但是大家可以去网上看看。无模型控制是我们中国学者提出的，但也是非常复杂的）。

基于ESO的MFC： （也就是本文提出的模型）

MFC的超局部模型：

        基于ESO的MFC方程如上，这个方程其实和上面的第一个式子没啥区别。可以看到这个F相当于把电阻压降、电动势、电感都看成扰动给归类进去了。α就是电感数值的倒数（这个需要注意一下！）。

ESO的表达式： 

        这个式子和我们上一节讲到的基于ESO的DPCC基本上是差不多的。注意到，我上一节讲DPCC的ESO时，电流误差e = 实际值-估计值。但是这篇文章是，电流误差e = 估计值-实际值，恰好是跟我的相反，所以这里会在e的前面出现负号。 

基于ESO的MFC表达式（连续域/s域）：

        这一步相当于是把上述的两步给结合了一下。

        这就相当于把MFC中的ESO模块给搭建出来了。那这个观测器是否是稳定的，那还得证明一下。

ESO的稳定性分析（连续域/s域）：

        这个稳定性证明是用了特征方程去判断，这和我们上一篇文章证明ESO稳定的方法一模一样。 

基于ESO的MFC表达式（离散域/z域）：

        因为我们刚才建立的都是连续域模型，实际的电机控制系统都是离散的。所以这里要将上述的表达式进行离散化。这个表达式也跟上一节我们谈到的ESO-DPCC的表达式差不多，而且这个表达式要比上一篇文章的表达式简单一些。

 

ESO的稳定性分析（离散域/z域）： 

        上述已经分析了ESO在连续域的稳定性。现在分析一下ESO在离散域的稳定性。

        得到ESO的传递函数之后，就可以得到其特征方程如式（15）所示。根据式（15）即可求出ESO的极点。

        从式（17）实际上就可以分析出，ESO带宽w0与ESO离散域极点z的关系了。

         

        文章中有解释到，w0越大，z越接近于0，那么系统的动态性能就越好。为什么会这样呢？w0越大，ESO在s域上的截止频率就越大，截止频率越大，那么系统的动态性能就越好（有很多文章已经做了ESO在s域上的伯德图，大家有兴趣的话可以自己去查阅一下）。在z域上，极点z越靠近0，系统的动态响应就越快。

        这样看来，文章的分析也是符合基本的控制理论知识。

 

参考电压的计算：

        建立好ESO的模型之后，就该想想怎么把ESO观测器出来的数据给利用起来。

        电机系统的参考电压可以通过式子（20）给计算出来，式子中的is(k+1)和F(k+1)都是由式子（13）估计出来的。

        总结一下：基于ESO的无模型预测电流控制，只需要两个参数，第一个是ESO的离散域的极点z，第二个是α。

        ESO的极点z，一般配置在0.5左右就差不多了。（文章中配置在z=0.15，这个数值已经非常接近于0了，所以动态性能很好。但是，对于不同的电机，配置在z=0.15的ESO，有可能使系统不稳定）

        超局部模型的α，在文章中一开始就提到了，一般选取为电感的倒数。但是这样想想，岂不是又需要电感的参数了吗？实际上，这个α不取为电感的倒数时，系统也会有较好的性能，反正自己取的大概就行了。文章中取了α＝50，我自己仿真中取了α＝200.

基于ESO的MFC的控制框图：

 

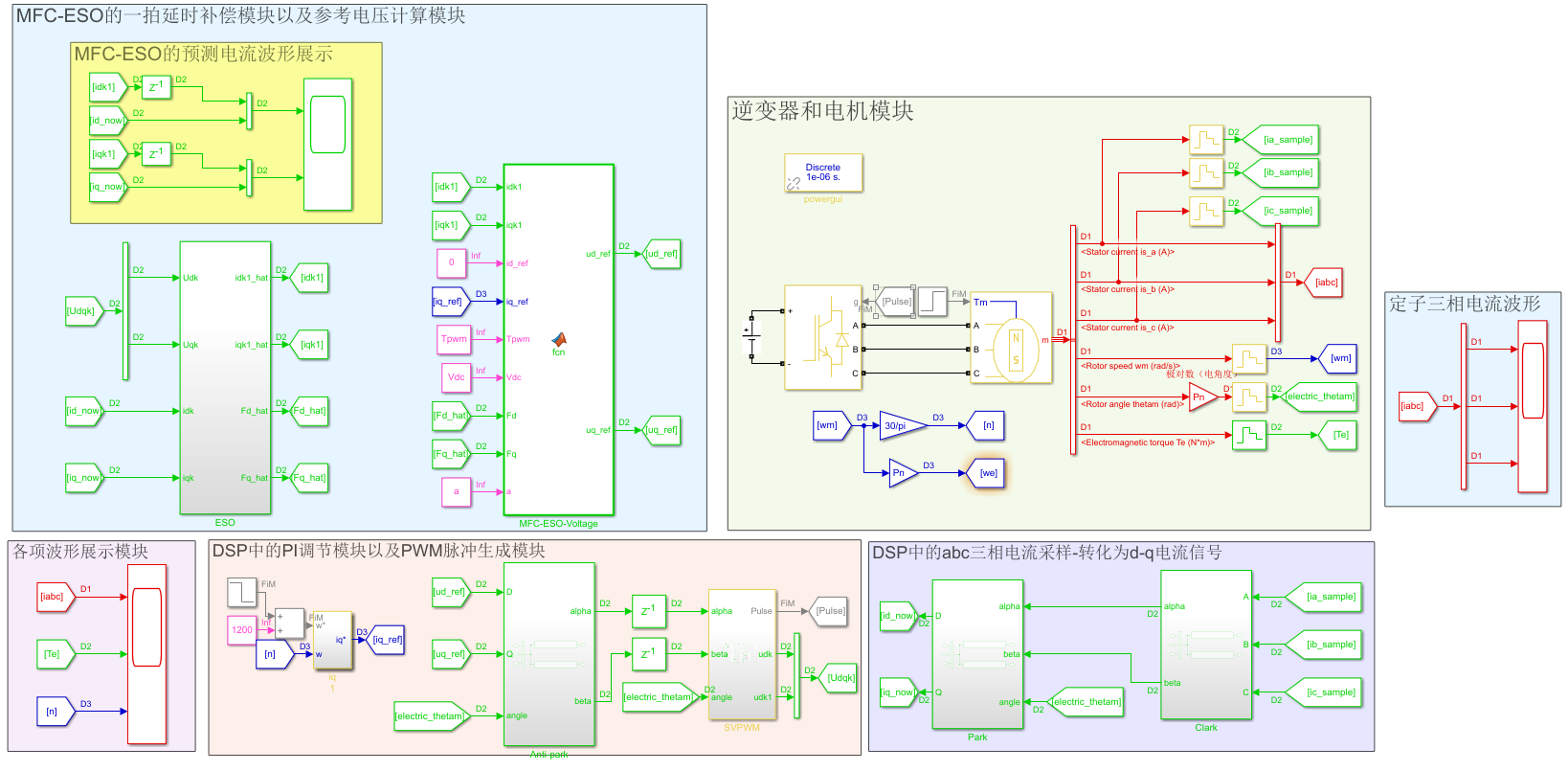
仿真展示：

这个是参考电压计算模块的代码，看起来就比基于ESO的DPCC简单了很多。

ESO的内部结构如下：（大家可以对比一下上一篇内容，这个ESO模块比DPCC的ESO模块简单了非常多）

 

 

仿真参数：

Tpwm = 1e-4;%开关周期

Tspeed = 5e-4;%转速采样周期，在实际DSP系统中，Tspeed会小于Tpwm

Pn = 4;%电机极对数

Vdc = 311;%直流母线电压

iqmax = 30;%额定电流

%这是电机实际参数

Ls = 8.5e-3;%定子电感，采用隐极的，Ld=Lq=Ls

Rs = 3;%定子电阻

flux = 0.1688;%永磁体磁链

%扩展观测器极点参数配置

c1 = 2*(5000);  %这是根据论文取极点z=0.5计算出来的

c2 = (5000)^2;

a = 200;   %这个就是α，文章中取50，我这里自己改的，大家随意调一下就好了

仿真波形：（仿真条件：电机空载启动，给定转速为1200r/min；在0.5s时加5N·m负载；在0.35s时，给定转速改为1000r/min。）

 

        从仿真中可以看到，三相电流在启动时没有超过额定值30A，系统也确实具有较好的动态响应能力。 

 

        从上图中可以看到，即使不采用任何的电机参数，ESO依旧能够很好地观测电流。也说明了本文所配置地参数的准确性。

接下来进行一下对比的仿真。使用的控制模型有：1.基于PI调节器的传统FOC；2.无差拍预测电流控制（无参数失配）；3.基于ESO的无模型预测控制。

稳态相电流THD：

 

 

         

        仿真中可以看到，基于ESO的无模型预测控制的相电流THD高了0.1%，高了一点点，而其他两种方法是都是2.28%。但是基于ESO的无模型预测控制的好处是不需要电机参数！别忘了，在PI调节器进行前馈补偿的时候，也需要电机参数的。上述三个模型中，只有基于ESO的无模型预测控制完完全全不需要任何参数！

        所以当电机参数失配的时候，基于PI调节器的传统FOC和无差拍预测电流控制的性能都将会下降，因此当然是基于ESO的无模型预测控制具有更大优势！

动态性能对比：

 

        从上述仿真中可以看出：无差拍预测电流控制（无参数失配）具有最快的动态性能，当然这也仅局限于参数不失配的情况下。基于ESO的无模型预测控制具有与无差拍预测电流控制（无参数失配）相近的动态性能。基于PI调节器的传统FOC的动态响应最慢，从图中可以看出，启动时，q轴流超过了最大值30A，而且具有一定的超调，消除超调的时间也比较长！

总结一下：

        基于ESO的无模型预测控制的优势：1结构简单。不像DPCC以及基于ESO的DPCC那样复杂、也不需要繁琐的PI调参。2.鲁棒性强。该方法完全不需要电机参数，完全吊打传统的DPCC；传统的PI调节器也会需要电机参数进行前馈补偿；PI调节器配置的时候一般用到零极点对消法，这个也需要电机参数。3.动态性能好。