实战——OPenPose讲解及代码实现

一些细节例如匈牙利匹配算法、PAF权值计算、模型结构改进等在这里并没有过多介绍；并且对于现在OPenpoe的使用，主要是将其编译成一个库，作为Python程序的调用；并且相比于本次的代码，其实时性很好，符合大部分落地场景的需求；如果有想要本次项目源码的，可以在评论区留下邮箱，也欢迎大家一起讨论，后续也会探讨更多最新的技术；

一个热爱学习的深度渣渣

4736人浏览 · 2023-08-14 18:54:32

一个热爱学习的深度渣渣 · 2023-08-14 18:54:32 发布

一些前提

先思考下面几个问题；

1、什么是姿态估计？

参考：Point Detect任务，识别人体指定部分的关键点；

2、姿态估计中的难点是什么？

从干扰的角度，人体被遮挡对检测的影响很大；

如何对检测的点进行匹配拼接，并且是顺序拼接，而且确保是同一个人；

怎么提升性能，算法能够实时推理；

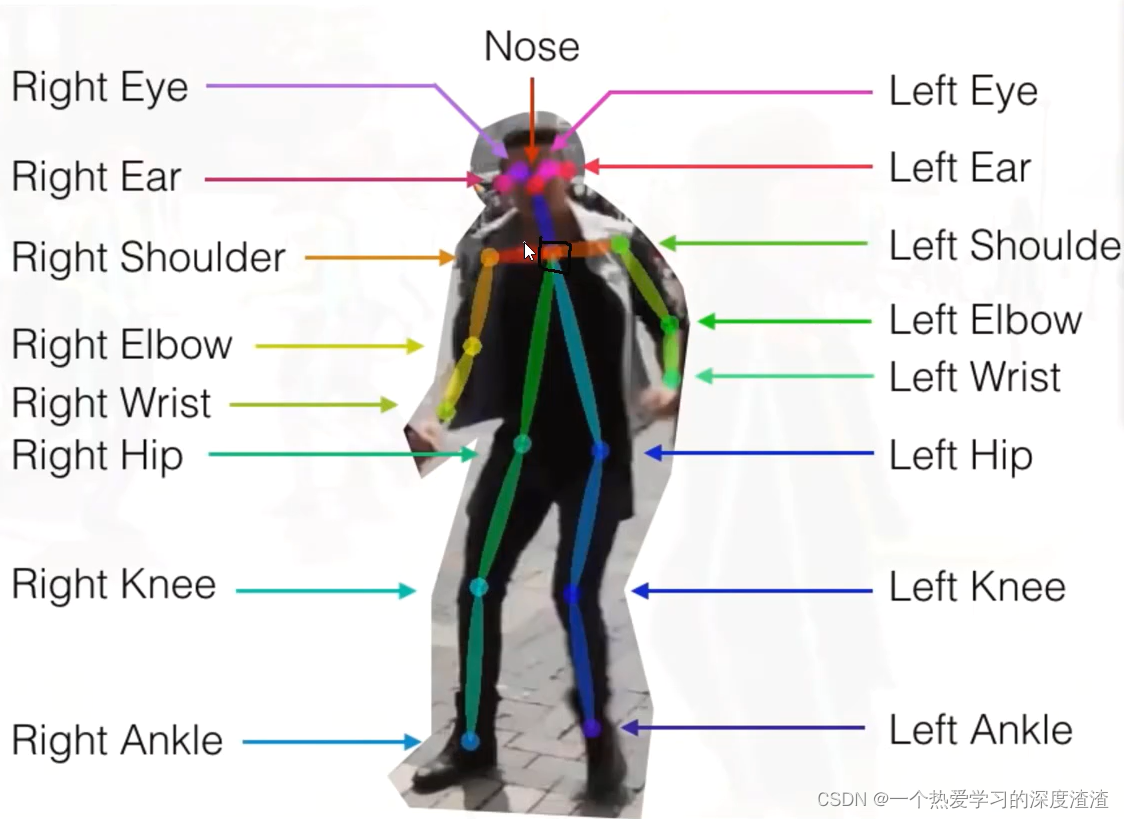
3、COCO数据集的关键点有几个，分别是？

在这里插入图片描述

数据集中是17个点，实际上训练时候还要加上一个脖子的点，通过两个肩膀的点计算；

4、应用领域有哪些？

运动领域：例如健身动作识别；
安全领域：路面防摔跤、游泳池溺水；
特殊需求：比如是否佩戴某件物品，可以根据关键点和物体的定位；

5、姿态估计方法分为几个大类？

Top-down（自顶向下）：先检测所有的人，再对每个框的人进行姿态估计输出结果

优点：准确率高，点的回归率高；

缺点：算法性能依赖检测效果，复杂度较高，实时性比较差；

主要用于一些离线的项目，对实时性没要求！！！
bottom-up（自底向上）：先检测所有关键点，再进行匹配连接

优点：计算量较小，可以达到实时性的效果；

缺点：精度较差，匹配策略比较复杂；

论文解读

论文地址：https://arxiv.org/pdf/1611.08050.pdf

参考文章：https://zhuanlan.zhihu.com/p/514078285

首先看一下整体的流程图：

在这里插入图片描述

首先输入一张W * H的图像进入网络，网络会有两个分支：

一是关键点检测，会生成一个热力图，检测出J个标签部位的点；

二是得到关键点的方向关系，也被称为PAF，对于每一个关键点都有其亲和域的方向；

最终结合二者，将所有关键点连接起来，输出一个完整的人体骨架；

算法流程

重点的关注点：

1、关键点的heatmap标注生成，采用高斯函数；

2、PAF：部分亲和域，文章提出的重要方法；

3、匹配策略：匈牙利匹配；

1、数据制作

采用的数据集为COCO数据集，其中人体骨骼点的标注信息为【x，y，label】，这里的label取值为0、1、2，分别表示不存在、遮挡、正常，其中不存在的关键点是需要去除的；

关键点高斯热力图实现：

def putGaussianMaps(center, accumulate_confid_map, sigma, grid_y, grid_x, stride):

    start = stride / 2.0 - 0.5
    y_range = [i for i in range(int(grid_y))]
    x_range = [i for i in range(int(grid_x))]
    xx, yy = np.meshgrid(x_range, y_range)      # 构建棋盘
    xx = xx * stride + start                    # 每个点在原始图像上的位置
    yy = yy * stride + start
    d2 = (xx - center[0]) ** 2 + (yy - center[1]) ** 2  # 计算每个点和GT点的距离
    exponent = d2 / 2.0 / sigma / sigma                 # 这里在做一个高斯计算
    mask = exponent <= 4.6052                           # 将在这个阈值范围内的点用True记录
    cofid_map = np.exp(-exponent)                       # 这里做一个标准化
    cofid_map = np.multiply(mask, cofid_map)            # 取出对应关系为True的点
    accumulate_confid_map += cofid_map                  # 将每个点计算的结果都累加到上一次的特征中
    accumulate_confid_map[accumulate_confid_map > 1.0] = 1.0      # 对结果大于1的值，只取1
    
    return accumulate_confid_map    # 返回热力图（heatmap）

PAF数据计算的实现：

def putVecMaps(centerA, centerB, accumulate_vec_map, count, grid_y, grid_x, stride):
    centerA = centerA.astype(float)
    centerB = centerB.astype(float)

    thre = 1  # 表示宽度，也就是一个设定好的参数
    centerB = centerB / stride  # 缩放比例特定到特征图中
    centerA = centerA / stride

    limb_vec = centerB - centerA  # 求出两个点的向量
    norm = np.linalg.norm(limb_vec)  # 是需要求单位向量，所以先计算范数，也就是向量模长
    if (norm == 0.0):  # 这里表示两个点基本重合了
        # print 'limb is too short, ignore it...'
        return accumulate_vec_map, count
    limb_vec_unit = limb_vec / norm  # 向量除以模长，得到单位向量
    # print 'limb unit vector: {}'.format(limb_vec_unit)

    # To make sure not beyond the border of this two points
    # 得到所有可能存在方向的区域(这里就用到了之前的超参数阈值)
    min_x = max(int(round(min(centerA[0], centerB[0]) - thre)), 0)
    max_x = min(int(round(max(centerA[0], centerB[0]) + thre)), grid_x)
    min_y = max(int(round(min(centerA[1], centerB[1]) - thre)), 0)
    max_y = min(int(round(max(centerA[1], centerB[1]) + thre)), grid_y)

    # 得到一个可能存在向量的矩形框
    range_x = list(range(int(min_x), int(max_x), 1))
    range_y = list(range(int(min_y), int(max_y), 1))
    xx, yy = np.meshgrid(range_x, range_y)  # 制作一个网格
    ba_x = xx - centerA[0]  # the vector from (x,y) to centerA 根据位置判断是否在该区域上（分别得到X和Y方向的）
    ba_y = yy - centerA[1]
    # 向量叉乘根据阈值选择赋值区域，任何向量与单位向量的叉乘即为四边形的面积
    # 这里是重点步骤，也就是论文中的公式，表示计算出两个向量组成四边形的面积
    limb_width = np.abs(ba_x * limb_vec_unit[1] - ba_y * limb_vec_unit[0])
    mask = limb_width < thre  # mask is 2D （小于阈值的表示在该区域上）

    vec_map = np.copy(accumulate_vec_map) * 0.0  # 构建一个全为0的矩阵

    # 这行代码主要作用是将mask扩展一个维度并且赋值给vec_map数组
    vec_map[yy, xx] = np.repeat(mask[:, :, np.newaxis], 2, axis=2)
    # 在该区域上的都用对应的方向向量表示（根据mask结果表示是否在，通过乘法的方式）
    vec_map[yy, xx] *= limb_vec_unit[np.newaxis, np.newaxis, :]

    # #在特征图中（46*46）中 哪些区域是该躯干所在区域，判断x或者y向量都不为0
    mask = np.logical_or.reduce(
        (np.abs(vec_map[:, :, 0]) > 0, np.abs(vec_map[:, :, 1]) > 0))

    # 每次返回的accumulate_vec_map都是平均值，现在还原成实际值
    accumulate_vec_map = np.multiply(
        accumulate_vec_map, count[:, :, np.newaxis])
    accumulate_vec_map += vec_map  # 加上当前关键点位置形成的向量
    count[mask == True] += 1  # 该区域计算次数都+1

    mask = count == 0

    count[mask == True] = 1  # 没有被计算过的地方就等于自身（因为一会要除法）

    accumulate_vec_map = np.divide(accumulate_vec_map, count[:, :, np.newaxis])  # 算平均向量
    count[mask == True] = 0  # 还原回去

    return accumulate_vec_map, count