SPSS软件的数据分析与GDP和人口老龄化的预测
利用spss软件分析人口老年化和GDP增长之间的关系,建立时间序列模型对第八次人口普查时的老龄化和GDP进行预测
目录
模型的检验
前言
SPSS软件的数据分析与GDP和人口老龄化的预测
下图是第七次人口普查的统计报告,显示1953年到2020年间7次人口普查的人口年龄段分布,下表是每次人口普查GDP情况,请用SPSS软件进行数据分析,完成以下题目:
1.分析人口老龄化与GDP增长是否有联系,如果有,请拿出数据进行相关说明;如果没有,请给出理由(65岁以上视为老龄人)。
2.请你根据图和表中所给数据预测第八次人口普查时,中国的人口老龄化情况,并对GDP进行预测(以每次普查为单位)。

| 每次人口普查的GDP 单位:美元 | |
| 年份 | GDP |
| 1953 | 314.86亿 |
| 1964 | 597.08亿 |
| 1982 | 2050.9亿 |
| 1990 | 3608.58亿 |
| 2000 | 1.21万亿 |
| 2010 | 6.09万亿 |
| 2020 | 14.72万亿 |
数据来源:国家统计局
- 模型的建立与求解
- 问题一模型的建立与求解
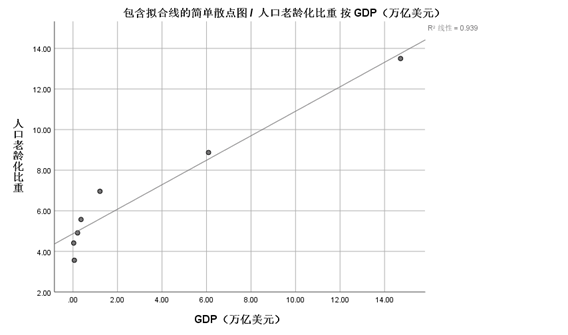
以GDP为横坐标,人口老龄化比重为纵坐标,画出散点图:

图一 GDP与人口老龄化比重的散点图
利用spss软件分析人口老龄化,即65岁以上所占人口比例与GDP之间的相关性,得出以下结果:
| 人口老龄化比重 | GDP | |||
| 肯德尔 tau_b | 人口老龄化比重 | 相关系数 | 1.000 | .905** |
| N | 7 | 7 | ||
| GDP | 相关系数 | .905** | 1.000 | |
| N | 7 | 7 | ||
| 斯皮尔曼 Rho | 人口老龄化比重 | 相关系数 | 1.000 | .964** |
| N | 7 | 7 | ||
| GDP | 相关系数 | .964** | 1.000 | |
| N | 7 | 7 | ||
| 相关性显著 | ||||
可以得出人口老龄化增长与GDP增长之间相关性显著
- 假设二者之间符合线性回归模型
即二者之间满足关系式:
利用spss软件进行数据分析,求出系数值:
| 系数a | ||||||
| 模型 | 未标准化系数 | 标准化系数 | t | 显著性 | ||
| B | 标准错误 | Beta | ||||
| 1 | (常量) | 4.872 | .415 | 11.732 | .000 | |
| GDP(万亿美元) | .603 | .069 | .969 | 8.774 | .000 | |
| a. 因变量:人口老龄化比重 | ||||||
可以得出人口老龄化增长与GDP增长之间的函数关系为:
画出回归曲线:

图二 线性拟合结果
- 假设二者之间符合非线性回归模型
利用matlab拟合工具箱,拟合出最佳曲线:

图三 非线性拟合结果
得出模型表达式为:
进行模型检验:
表一 模型检验结果
| 稳态误差 | 多重测定系数 | 拟合系数 | 剩余标准差 |
| 2.03 | 0.9712 | 0.9568 | 0.7125 |
因此可认为拟合效果较好。
问题二模型的建立与求解
1.2.1 ARIMA时间序列模型的建立与求解
列出各年份对应的人口老龄化比重和GDP如下表所示:
表二 各年份对应的人口老龄化比重和GDP
| 年份 | 人口老龄化比重 | GDP |
| 1953.00 | 4.41 | 0.03 |
| 1964.00 | 3.56 | 0.06 |
| 1982.00 | 4.91 | 0.21 |
| 1990.00 | 5.57 | 0.36 |
| 2000.00 | 6.96 | 1.21 |
| 2010.00 | 8.87 | 6.09 |
| 2020.00 | 13.50 | 14.72 |
平稳性检验
画出人口老龄化比重和GDP对应的时序图进行初步检验:


图四 时序图
观察时序推测两项时序图均为非平稳序列,进一步进行Daniel检验.
Spearman相关系数:

记人口老龄化比重和GDP对应的时间序列分别为
对于显著水平0.05,由Spearman相关系数计算公式可得两个时间序列均为非平稳序列,因此构造差分序列:

画出各一阶差分方程所对应的散点图:

图五 人口老龄化对应时序图

图六 GDP对应时序图
由散点图可知,序列较为平稳,而
所在的序列无论进行多少次差分均无法平稳,故对于无法使用时间序列求解
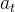 的时间序列预测模型的建立与求解
的时间序列预测模型的建立与求解
建立如下的ARIMA模型对进行预测:

利用表中数据,采用最小二乘法计算得出的预测模型为:

则得出第八次人口普查老龄化比重的预估值为:14.41.
模型的检验
绘出预测模型中的数据与实际数据进行对比:

图七 人口老龄化预测模型结果
由图可知该模型准确率较高,结果具有可信度
对于的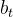 时间序列预测模型的建立与求解
时间序列预测模型的建立与求解
由于无法直接对使用时间序列求解,但所建模型求解精度较高,故可用第一题拟合方程对进行求解:

代入,可得出
的表达式:

得出第八次人口普查的GDP的预估值为18.896(万亿美元)
模型的检验

图八 GDP预测结果
由图可知由于GDP增长速度逐年增加,国家对于老龄化问题处理的更好,故该结果可信度并不高。即该模型是存在缺陷的

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容





所有评论(0)