基于simulink的无人机姿态飞行控制仿真
无人机是无人驾驶飞机的简称(Unmanned Aerial Vehicle),是利用无线电遥控设备和自备的程序控制装置的不载人飞机,包括无人直升机、固定翼机、多旋翼飞行器、无人飞艇、无人伞翼机。飞控子系统是无人机完成起飞、空中飞行、执行任务和返场回收等整个飞行过程的核心系统,飞控对于无人机相当于驾驶员对于有人机的作用,我们认为是无人机最核心的技术之一。飞控一般包括传感器、机载计算机和伺服作动设备三
目录
1.算法描述
无人机是无人驾驶飞机的简称(Unmanned Aerial Vehicle),是利用无线电遥控设备和自备的程序控制装置的不载人飞机,包括无人直升机、固定翼机、多旋翼飞行器、无人飞艇、无人伞翼机。广义地看也包括临近空间飞行器(20-100 公里空域),如平流层飞艇、高空气球、太阳能无人机等。从某种角度来看,无人机可以在无人驾驶的条件下完成复杂空中飞行任务和各种负载任务,可以被看做是 “空中机器人”。
飞控子系统是无人机完成起飞、空中飞行、执行任务和返场回收等整个飞行过程的核心系统,飞控对于无人机相当于驾驶员对于有人机的作用,我们认为是无人机最核心的技术之一。飞控一般包括传感器、机载计算机和伺服作动设备三大部分,实现的功能主要有无人机姿态稳定和控制、无人机任务设备管理和应急控制三大类。
对于固定翼无人机,一般来说,在姿态平稳时,控制方向舵会改变飞机的航向,通常会造成一定角度的横滚,在稳定性好的飞机上,看起来就像汽车在地面转弯一般,可称其为测滑。方向舵是最常用做自动控制转弯的手段,方向舵转弯的缺点是转弯半径相对较大,较副翼转弯的机动性略差。 副翼的作用是进行飞机的横滚控制。固定翼飞机当产生横滚时,会向横滚方向进行转弯,同时会掉一定的高度。 升降舵的作用是进行飞机的俯仰控制,拉杆抬头,推杆低头。拉杆时飞机抬头爬升,动能朝势能的转换会使速度降低,因此在控制时要监视空速,避免因为过分拉杆而导致失速。 油门舵的作用是控制飞机发动机的转速,加大油门量会使飞机增加动力,加速或爬升,反之则减速或降低。
了解了各舵的控制作用,我们开始讨论一下升降舵和油门的控制。固定翼飞机都有一个最低时速被称做失速速度,当低于这个速度的时候飞机将由于无法获得足够的升力而导致舵效失效,飞机失控。通过飞机的空速传感器我们可以实时获知飞机的当前空速,当空速降低时必须通过增加油门或推杆使飞机损失高度而换取空速的增加,当空速过高时减小油门或拉杆使飞机获得高度而换取空速的降低。因此固定翼飞机有两种不同的控制模式,根据实际情况的使用而供用户选择: 第一种控制方式是,根据设定好的目标空速,当实际空速高于目标空速时,控制升降舵拉杆,反之推杆;那空速的高低影响了高度的高低,于是采用油门来控制飞机的高度,当飞行高度高于目标高度时,减小油门,反之增加油门。由此我们可以来分析,当飞机飞行时,如果低于目标高度,飞控控制油门增加,导致空速增加,再导致飞控控制拉杆,于是飞机上升;当飞机高度高于目标高度,飞控控制油门减小,导致空速减小,于是飞控再控制推杆,使高度降低。这种控制方式的好处是,飞机始终以空速为第一因素来进行控制,因此保证了飞行的安全,特别是当发动机熄火等异常情况发生时,使飞机能继续保持安全,直到高度降低到地面。这种方式的缺点在于对高度的控制是间接控制,因此高度控制可能会有一定的滞后或者波动。 第二种控制方式是:设定好飞机平飞时的迎角,当飞行高度高于或低于目标高度时,在平飞迎角的基础上根据高度与目标高度的差设定一个经过PID控制器输出的限制幅度的爬升角,由飞机当前的俯仰角和爬升角的偏差来控制升降舵面,使飞机迅速达到这个爬升角,而尽快完成高度偏差的消除。但飞机的高度升高或降低后,必然造成空速的变化,因此采用油门来控制飞机的空速,即当空速低于目标空速后,在当前油门的基础上增加油门,当前空速高于目标空速后,在当前油门的基础上减小油门。这种控制方式的好处是能对高度的变化进行第一时间的反应,因此高度控制较好,缺点是当油门失效时,比如发动机熄火发生时,由于高度降低飞控将使飞机保持经过限幅的最大仰角,最终由于动力的缺乏导致失速。 因此,两种控制模式根据实际情况而选用。我们选用的是第二种控制模式,并增加了当空速低于一定速度的时候,认为异常发生,立刻转为第一种控制模式以保证飞机的安全。
simulink是基于matlab的框图设计环境,可以用来对各种动态系统进行建模、分析和仿真,它的应用领域十分广泛,任何能用数学模型来描述的系统都可以在simulink中进行仿真分析,如:空气动力学、导航制导、通讯、电子、机械、热力学等诸多领域,这些系统从数学角度来描述多涉及连续、离散、非线性、时变、条件执行、多速率混合等用解析方法难以求解的系统,他们都可以通过simulink进行建模与仿真,从而指导系统的分析与设计。
simulink的特点
1.交互式建模:提供大量功能模块便于用户快速建立模型,建模仅需利用鼠标拖放功能块并将其连接起来。
2.交互式仿真:仿真结果可以动态显示,并可以在仿真过程中随时修改参数。
3.扩展与定制:提供了一个开放式的环境,允许用户扩充功能,可以将C、 fortran编写的算法集成到框图中。
4.专业的模型库:针对不同行业和领域提供了专业模型库
Simulink具有适应面广、结构和流程清晰及仿真精细、贴近实际、效率高、灵活等优点,并基于以上优点Simulink已被广泛应用于控制理论和数字信号处理的复杂仿真和设计。同时有大量的第三方软件和硬件可应用于或被要求应用于Simulink。
Simulink可以用连续采样时间、离散采样时间或两种混合的采样时间进行建模,它也支持多速率系统,也就是系统中的不同部分具有不同的采样速率。为了创建动态系统模型,Simulink提供了一个建立模型方块图的图形用户接口,这个创建过程只需单击和拖动鼠标操作就能完成,它提供了一种更快捷、直接明了的方式,而且用户可以立即看到系统的仿真结果。
Simulink是用于动态系统和嵌入式系统的多领域仿真和基于模型的设计工具。对各种时变系统,包括通讯、控制、信号处理、视频处理和图像处理系统,Simulink提供了交互式图形化环境和可定制模块库来对其进行设计、仿真、执行和测试。.
构架在Simulink基础之上的其他产品扩展了Simulink多领域建模功能,也提供了用于设计、执行、验证和确认任务的相应工具。Simulink与MATLAB紧密集成,可以直接访问MATLAB大量的工具来进行算法研发、仿真的分析和可视化、批处理脚本的创建、建模环境的定制以及信号参数和测试数据的定义。
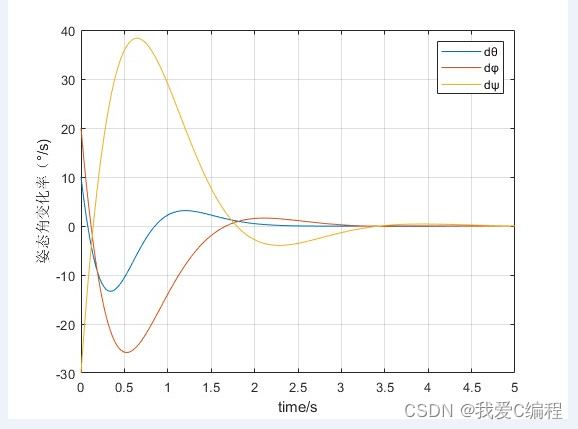
2.仿真效果预览
matlab2022a仿真结果如下:


3.MATLAB核心程序

function [sys,x0,str,ts] = Attitude7(t,x,u,flag,J)
switch flag,
case 0,
[sys,x0,str,ts]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u,J);
case {2,4,9},
sys=[];
case 3,
sys=mdlOutputs(t,x);
otherwise
error(['Unhandled flag = ',num2str(flag)]);
end
function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 6;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 6;
sizes.NumInputs = 3;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
% w0=[10 ;20 ;-30];
% theta0=[10 ;20 ;-30];
x0=[10 20 -30 10 20 -30]/180*pi;
str = [];
ts = [0 0];
%---状态方程----姿态运动学和动力学方程-----
function sys=mdlDerivatives(t,x,u,J)
J1=J(1);J2=J(2);J3=J(3);
w1=x(1);w2=x(2);w3=x(3);
theta1=x(4);theta2=x(5);theta3=x(6);
%--------------------
dw1=(J2-J3)/J1*w3*w2+1/ J1*u(1);
dw2=(J3-J1)/J2*w1*w3+1/ J2*u(2);
dw3=(J1-J2)/J3*w1*w2+1/ J3*u(3);
dtheta1=w1-w2*cos(theta1)*tan(theta3)+w3*sin(theta1)*tan(theta3);
dtheta2=w2*cos(theta1)/cos(theta3)-w3*sin(theta1)/cos(theta3);
dtheta3=w2*sin(theta1)+w3*cos(theta1);
%-----------------------
sys =[dw1 dw2 dw3 dtheta1 dtheta2 dtheta3];
function sys=mdlOutputs(t,x)
wx=x(1);wy=x(2);wz=x(3);
thetax=x(4);thetay=x(5);thetaz=x(6);
% % dthetax=wx-wy*cos(thetax)*tan(thetaz)+wz*sin(thetax)*tan(thetaz);
% % dthetay=wy*cos(thetax)/cos(thetaz)-wz*sin(thetax)/cos(thetaz);
% % dthetaz=wy*sin(thetax)+wz*cos(thetax);
% wx=x(1);wy=x(2);wz=x(3);
% thetax=x(4);thetay=x(5);thetaz=x(6);
sys =[wx wy wz thetax thetay thetaz];
A2404.完整MATLAB
V

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容





所有评论(0)