利用卡尔曼滤波处理超声波数据

---

前言

上节我们通过中断捕获，得到了超声波返回的数据，但可以看到，由超声波模块返回的数据含有噪音，这次，我们将使用卡尔曼滤波去处理超声波的数据，使得在后续的处理中更加方面和稳定。
STM32 Cubemax(九) ——利用输入捕获中断实现超声波测距

一、卡尔曼滤波

如果对卡尔曼滤波没有了解的同学，建议看看下面的视频，个人感觉讲的比较清楚和透彻。
【官方中字】什么是卡尔曼滤波器 (Kalman Filters) ？(全7P) MATLAB&Simulink

我们这里重点讲如何应用卡尔曼滤波的五个方程到我们实际中。

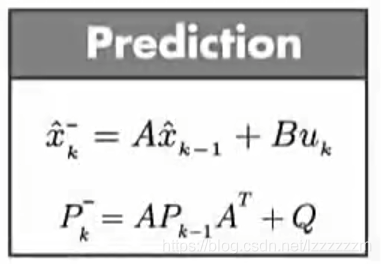
1.预测方程

第一个方程

第一个方程表示的是——当前最优的先验预测值 = 上一次的最优后验值 + 当前的输入值
参数含义：A表示的是 NxN 的状态转移矩阵，B是当前输入增益矩阵。
在我们超声波的案例，A是等于一的，因为我们是静态测量，正常来说，当前的值应该和上一次的值没有很大区别。如果我们不是静态测量，假如是具有匀速运动关系。则我们这时候的x最优估计值包含位置p和速度v两个参量， 根据运动公式可以等到下式。

而我们的整个系统是不存在输入的，则B等于0。
—————————————————————————————————————————————

第二个方程

第二个方程表示的是——当前预测协方差矩阵 = 上一次的最优协方差矩阵 + 过程噪声
参数含义：这个方程的公式是由协方差矩阵的公式推导的。

其中Q代表过程噪声，也是我们卡尔曼滤波中需要调节的参数之一，其代表运动模型过程中忽略的噪声因素，比如小车在运动过程中，常常忽略摩擦力，而在我们本例超声波中，不存在明显的影响因素，可以直接设定为0
—————————————————————————————————————————————

2.更新方程

在讲更新方程前，还有一个方程为观测矩阵。

观测矩阵

这个方程代表的是——观测量 = 测量量 * 增益 + 测量噪声
在本实验中，我们的观测量即等于传感器测量的值，故H=1。举个例子，一个系统的位置P（x，y）由x的测量量和y的测量组成，此时既有

而测量噪声，则是传感器本身带有的噪声，是我们这次重点调参的对象。
—————————————————————————————————————————————

第三个方程

先说明一下，观察矩阵的H和卡尔曼增益计算中的C是同一个东西，不同的写法。
第三个方程即为卡尔曼增益的计算公式，这个参数本质上的意思相当于是一个比例，代表我们是相信预测值的比重大还是相信测量值的比重大的一个权重。
—————————————————————————————————————————————

第四个方程

第四个方程，即表示当前的最优值 = 预测值与测量值的一个权重比例加和。
如果更加相信预测值，此时卡尔曼增益Kg应该小。
如果更加相信测量值，此时卡尔曼增益Kg应该大
—————————————————————————————————————————————

第五个方程

第五个方程即为更新协方差矩阵。
在本实验中为一维数据，I=1
—————————————————————————————————————————————
以上就是本实验五个方程的讲解，只要根据次写代码就好了。

二、代码

1.创建有关卡尔曼滤波的结构体

typedef struct
{
		float lastP;		//上次的协方差
		float nowP;			//本次的协方差
		float x_hat;		//卡尔曼滤波的计算值，即为后验最优值
		float Kg;			//卡尔曼增益系数
		float Q;			//过程噪声
		float R;			//测量噪声
}Kalman;

2.初始化

void Kalman_Init()
{
		KF.Q = 0;			//过程噪声可以认为是0
		KF.R = 0.01;		//给一个较小的值，可以在debug中调节
		KF.Kg = 0;			
		KF.lastP = 1;		//lastP相当于上一次的值，初始值可以为1，不可以为0
		KF.x_hat = 0;		
}

3.一维卡尔曼滤波函数

void Kalman_Filter(Kalman *KF, float input)
{
		float output = 0, x_t;						//output为卡尔曼滤波计算值
		x_t = KF->x_hat;							//当前先验预测值 = 上一次最优值
		KF->nowP = KF->lastP + KF->Q;				//本次的协方差矩阵
		KF->Kg = KF->nowP / (KF->nowP + KF->R);		//卡尔曼增益系数计算
		output = x_t + KF->Kg*(input - x_t); 		//当前最优值
		KF->x_hat = output;							//更新最优值
		KF->lastP = (1 - KF->Kg) * KF->nowP;		//更新协方差矩阵
		
}

而后，我们就可以将超声波实验得到的值，放入卡尔曼滤波器中进行滤波。

实验结果

蓝线为卡尔曼滤波结果，黄线为原始值。

总结

可以看出卡尔曼滤波效果是十分好的，不过这仅是一维的滤波，而我们在实际应用中，其实二维使用的场景会更多。后续会更新相关二维的信息。