因果推断--Uplift model的原理和python实操（三）

目前精细化运营已经普及到各行各业，如何把营销成本投入到真正被运营策略打动的用户身上，而不浪费在本身就会转化用户身上，是精准营销面临的重要课题，也是提高投入产出比的重要手段，业界成熟的解决方法是Uplift Model。本文主要介绍Uplift Model的应用背景、原理及建模细节、python中如何实现。

sikadeerlu

5779人浏览 · 2023-07-18 11:00:03

sikadeerlu · 2023-07-18 11:00:03 发布

一、Uplift Model的应用场景

二、Uplift Model原理及建模方法

2.1 建模目标

2.2 建模方法

1. 双模型--差分响应模型

2. 标签转化--Class Transformation Method

一、Uplift Model的应用场景

目前精细化运营已经普及到各行各业，如何把营销成本投入到真正被运营策略打动的用户身上，而不浪费在本身就会转化用户身上，是精准营销面临的重要课题，也是提高投入产出比的重要手段。接下来结合营销四象限理论进一步说明如何解决这个问题：

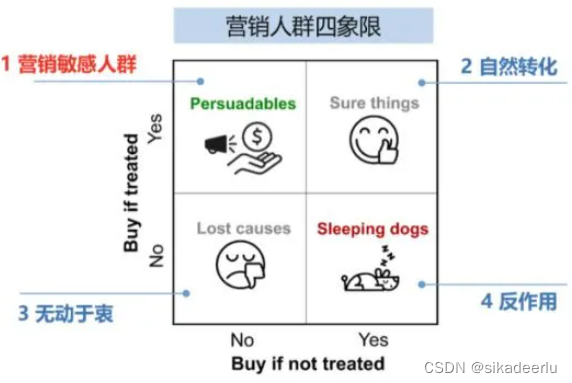
根据该理论，我们知道营销人群可以分为四大类，划分的依据是用户在干预和未干预情况下的表现：

营销敏感人群：有营销干预时转化，无营销干预时不转化。

自然转化人群：有无营销干预都会转化。

无动于衷人群：有无营销干预都不会转化。

反作用人群：无营销干预时转化，有营销干预时反而不转化，也就是营销厌恶人群。

对于以上问题，我们要识别的是营销敏感人群，把营销预算投入到这部分人群身上，才能带来“增量”效果。Uplift Model是业界较为成熟的解决该问题的方法，该模型是增益模型，预测的目标是策略干预下用户转化率的提升，提升越大说明越敏感。

二、Uplift Model原理及建模方法

2.1 建模目标

Uplift Model预测的是某种干预对个体状态或行为的因果效应，即ITE(individual treament effect)。用公式可表示为：

$p(Y_{i}|X_{i},T_{i} = 1) - p(Y_{i}|X_{i},T_{i} = 0)$

其中Y干预/未干预下的预测值，X是用户特征，T为是否干预。建模目标是用户在干预和未干预情况下的概率之差。与LR/RF/XGB/LGB等响应模型的区别是，这些模型预测的是某事件发生的概率，而Uplift Model要预测的是事件发生的概率提升值。建模难点是样本数据获取困难，无法同时获得一个用户在干预和未干预条件下的转化情况。但该问题可以通过AB实验解决，通过AB随机分流可以把个体的因果效应转化为群体的因果效应，即CATE :

$\tau(X_{i}) = E(Y_{i}(1) - Y_{i}(0)|X_{i})$

2.2 建模方法

1. 双模型--差分响应模型

即分别对实验组用户和对照组用户建模，预测用户在干预/未干预情况下的转化概率，对要预测的用户分别套入两个模型，两个概率做差，就能得到Uplift Score。如下是该模型详细的操作流程：

该模型的优点是建模简单，分别建立两个分类模型，用两个分类模型做差就能得到Uplift Score。

缺点是：两个模型容易积累误差；建模的目标是response而不是uplift，对uplift的识别较弱。

2. 标签转化--Class Transformation Method

该方法能打通实验组/对照组的数据和模型，可直接进行预测Uplift Score，即 $\tau ({X_{i}})$ 。定义变量Z，其取值如下：

$Z = \left\{\begin{matrix} 1 & if\, \displaystyle G = T \, and \, Y = 1\\ 1 & if \, G = C\, and \, Y = 0\\ 0 & otherwise \end{matrix}\right.\displaystyle$

预测 $\tau(X) = P^{T}(Y=1|X)-P^{C}(Y=1|X)$ ，可转化为预测 $p(Z = 1|X)$ 。详细的建模流程见下图：

转化为预测Z=1的推导过程如下，可选读。我们知道在AB实验中，用户特征和干预策略相互独立，所以有 $P(T|X) = P(T),P(C|X)=P(C)$ ，所以要预测的函数就能做如下转换：

$\begin{aligned} P(Z = 1|X) &= P(Z = 1|X,T)P(T|X) + P(Z=1|X,C)P(C|X) \\ &= P(Y = 1|X,T)P(T|X) + P(Y=0|X,C)P(C|X) \\ &= P^{T}(Y = 1|X)P(T) + P^{C}(Y=0|X)P(C) \end{aligned}$

同样在AB实验中，如果实验组和对照组的分流人数是相等的，则有 $P(T)=P(C)=\frac{1}{2}$ ，用户被分到实验组和对照组的概率是一样的，上式可转化为：

$\begin{aligned} P(Z = 1|X) &= P^{T}(Y = 1|X)P(T) + P^{C}(Y=0|X)P(C) \\ &= \frac{1}{2}P^{T}(Y = 1|X) + \frac{1}{2}P^{C}(Y=0|X) \\ &= \frac{1}{2}P^{T}(Y = 1|X) + \frac{1}{2}(1-P^{C}(Y=1|X)) \end{aligned}$

所以，我们的目标变量就可转化为如下形式：

$\begin{aligned} \tau(X) & = P^{T}(Y=1|X)-P^{C}(Y=1|X) \\ & = 2P(Z=1|X) - 1 \end{aligned}$

2.3 模型评估

对于响应模型来说，在测试集上我们有预测值和真实值，模型评估可以用auc、recall、precision等。但对于Uplift Model来说，我们无法同时获取到一个用户在干预和未干预下的转化概率，也就是ground truth，所以需要构造ground truth。如何构造呢，就是通过Uplift Score（这个是预测值）这一桥梁，拉齐同一得分区间的用户。这里边有实验和对照组用户，可以分别得到干预下的真实转化率和未干预下的真实转化率，两者做差就是真实的增益得分。

1. uplift 柱状图

在测试集上对预测出来的Uplift Score降序排列，划分十等份，在每一等分用户里边分别求实验组和对照组的转化率，两者相减即为真实的增益得分。这样就能绘制Uplift柱状图，可根据该图进行营销敏感人群的挑选，也能大概知道对TopN比例的用户进行营销干预能带来增量效果。

2. gini曲线

gini curve 是也是衡量uplift model效果的一种方法，可计算曲线下的面积作为AUUC(类似AUC)，其计算方法如下

和上述uplif 柱状图一样，准备好实验组、对照组十分位数据结果
计算 $Q(i) = \frac{ N_{t}(i)}{ N_{t}} - \frac{ N_{c}(i)}{ N_{c}}$ ，i 表示 top i%，即是top%多少的样本数据， $N_{t},N_{c}$ 表示实验组和对照组的总用户量， $N_{t}(i)$ 表示top i%的实验组用户中转化的用户数， $N_{c}(i)$ 表示top i%的对照组用户中转化的用户数。
以i%作为横坐标，Q(i)做为纵坐标形成的曲线，就是gini curve，其围成的面积就是 AUUC

三、python中如何实现

接下来看下如何在python中实现增益模型，以下代码使用的数据集来自kaggle：Marketing Promotion Campaign Uplift Modelling | Kaggle

以下代码在工作中的真实数据中有不错的表现，但在该数据集上的表现并不好，代码可做参考。

3.1 数据读入与简单描述性分析

%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
import xgboost as xgb
from sklearn.model_selection import train_test_split

import datetime

from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve, classification_report, roc_auc_score
from sklearn import metrics
from xgboost.sklearn import XGBClassifier
from xgboost import XGBClassifier
import xgboost as xgb
from sklearn.ensemble import RandomForestClassifier
import lightgbm
import graphviz
from sklearn import tree 
from sklearn.tree import DecisionTreeClassifier

# 1. 读入数据
# 该数据集 来源  https://www.kaggle.com/datasets/davinwijaya/customer-retention
data = pd.read_csv('./data.csv' )
data.head()


# 2.查看离散变量及取值
for column in data.drop(columns = ['recency', 'history']):
    print(column, '\n', data[column].value_counts(), '\n')

# 3.连续变量看分布
con_columns = ['recency', 'history']

fig = plt.figure(figsize = (16, 10))
ax1 = fig.add_subplot(121)
data['recency'].hist(ax = ax1)
ax1.set_title('recency distribution')

ax2 = fig.add_subplot(122)
data['history'].hist(ax = ax2)
ax2.set_title('history distribution')


# 4.目标变量及干预变量列名修改
df_model = data.rename(columns = {'conversion': 'target'})  # 目标变量
df_model = df_model.rename(columns = {'offer': 'treatment'})  # 是否干预

df_model.treatment = df_model.treatment.map({'No Offer': 0, 'Buy One Get One': -1, 'Discount': 1})  # treatment重新赋值

# 离散变量转为哑变量
df_model = pd.get_dummies(df_model)
df_model.head()

# 看不同干预条件下的转化情况
df_model.groupby('treatment').agg({'target': 'mean'})



# 5.定义方法：看各特征下转化率的提升
def get_every_group_up(data, dim, ab_tag):
    # 按输入维度 dim、ab分组字段 ab_tag 进行分组汇总件量和空运件量
    dim_data = data.groupby(by = [dim, ab_tag]).agg({'target': 'sum', 'treatment': 'count'})
    dim_data.columns = ['target', 'cnt']  # 将treatment 列名 赋值为 cnt 用户数
    dim_data['pct'] = dim_data['target']/dim_data['cnt']  # 空运件量占比
    

    # 计算各因素实验组和对照组的空运寄件率
    dim_data_b = dim_data.loc[(slice(None), -1), 'pct'].loc[:, -1]
    dim_data_a = dim_data.loc[(slice(None), 0), 'pct'].loc[:, 0]

    # 计算各因素分布情况
    dim_data_pct = data[dim].value_counts()/data[dim].count()

    dim_data_df = pd.concat([dim_data_pct, dim_data_a, dim_data_b], axis = 1)
    
    # 列重命名 占比 对照组转化率 实验组转化率
    dim_data_df.columns = ['proportion', 'pct_a', 'pct_b']
    dim_data_df['uplift'] = dim_data_df['pct_b'] - dim_data_df['pct_a']
    
    return dim_data_df


# 查看 recency 不同分段下 实验组（买一送一）与对照组（无优惠）转化率提升情况
uplift_data = df_model[df_model['treatment'].isin([-1, 0])]

uplift_data['recency_bins'], updown = pd.qcut(uplift_data['recency'], q = 5, retbins = True, duplicates = 'drop')
diff_recency_bins_df = get_every_group_up(uplift_data, 'recency_bins', 'treatment')
diff_recency_bins_df.style.background_gradient()

3.2 建模--双模型

公共方法

# 定义方法 画模型roc曲线 阈值等，模型调参时查看效果较方便
def plot_model_result(preds, y_test):
    # roc曲线相关指标
    FPR, recall, thresholds = roc_curve(y_test, preds, pos_label = 1)
    area = roc_auc_score(y_test, preds)
    
    plt.figure()
    plt.plot(FPR, recall, color = 'r', label = 'roc curve (area=%0.4f' % area)
    plt.plot([0, 1], [0, 1], color = 'black', linestyle = '--')
    maxindex = (recall - FPR).tolist().index(max(recall - FPR))
    plt.scatter(FPR[maxindex], recall[maxindex], c = 'black', s = 30)
    print('阈值', thresholds[maxindex])
    plt.xlim([-0.05, 1.05])
    plt.ylim([-0.05, 1.05])
    plt.xlabel('False Positive Rate')
    plt.ylabel('Recall')
    plt.title('ROC Curve')
    plt.legend(loc = 'best')
    plt.show()
    
    ypred = preds.copy() 
    ypred[preds > thresholds[maxindex]] = 1 
    ypred[ypred != 1] = 0
    print('classification_report \n',classification_report(y_test, ypred, digits=4))
#     print('confusion_matrix \n', confusion_matrix(y_test, ypred))
#     return thresholds[maxindex]  # 将阈值返回

建模

# 1. 模型数据准备 以其中 Buy One Get One 即 treatment = -1 为例
# 对照组 建模
uplift_data_a = uplift_data[uplift_data['treatment'] == 0].drop(columns = ['recency_bins', 'history_bins'])

# 实验组
uplift_data_b = uplift_data[uplift_data['treatment'] == -1].drop(columns = ['recency_bins', 'history_bins'])

x_a = uplift_data_a.loc[:, uplift_data_a.columns.difference(['treatment', 'target'])]
y_a = uplift_data_a['target']


# 划分训练集与测试集
x_train_a, x_test_a, y_train_a, y_test_a = train_test_split(x_a, y_a, test_size = 0.4, random_state = 20000)

# 建模 这里以 RandomForest 为例
clf_rf_a = RandomForestClassifier(n_estimators = 100, random_state = 200, max_depth = 10, min_samples_leaf = 10)
clf_rf_a.fit(x_train_a, y_train_a)

# 在测试集上预测并看效果
y_pre_test_a = clf_rf_a.predict_proba(x_test_a)
plot_model_result(y_pre_test_a[:, 1], y_test_a)



# 实验组建模 和 对照组建模类似
# lgb 模型数据集 实验组
x_b = uplift_data_b.loc[:, uplift_data_a.columns.difference(['treatment', 'target'])]
y_b = uplift_data_b['target']

x_train_b, x_test_b, y_train_b, y_test_b = train_test_split(x_b, y_b, test_size = 0.4, random_state = 20000)

clf_rf_b = RandomForestClassifier(n_estimators = 100, random_state = 200, max_depth = 10, min_samples_leaf = 10)
clf_rf_b.fit(x_train_b, y_train_b)

y_pre_test_b = clf_rf_b.predict_proba(x_test_b)
plot_model_result(y_pre_test_b[:, 1], y_test_b)

3.3 uplift 柱状图

# 1.测试集上的实验组、对照组分别拿两个模型预测
# pre_a 是 对照组用户x_valid_a  在没有干预情况下的寄件率，用实验组 模型 model_b 得到在有干预的情况下的空运寄件率
pre_a_under_b_model = clf_rf_b.predict_proba(x_test_a)


# pre_b 是 实验组用户 x_valid_b 在有干预情况下的寄件率，用对照组 模型 model_a 得到在没有干预情况下的空运寄件率
pre_b_under_a_model = clf_rf_a.predict_proba(x_test_b)


# 2.实验组、对照组数据集分别添加以上两预测值
# 对照组：将两种情况下的寄件率拼接到 对应的数据集
x_test_a['pre_a'] = y_pre_test_a[:,0]
x_test_a['pre_b'] = pre_a_under_b_model[:,0]
x_test_a.head()

test_a = pd.concat([x_test_a, y_test_a], axis = 1)
test_a.head()


# 实验组：将两种情况下的寄件率拼接到 对应的数据集上,
x_test_b['pre_a'] = y_pre_test_b[:,0]
x_test_b['pre_b'] = pre_b_under_a_model[:,0]
x_test_b.head()

test_b = pd.concat([x_test_b, y_test_b], axis = 1)
test_b.head()


# 3.计算预测出的uplift score
test_a['uplift_score'] = test_a['pre_b'] - test_a['pre_a']
test_b['uplift_score'] = test_b['pre_b'] - test_b['pre_a']

# 4.合并两组数据，一起划分十分位
test_ab_all = pd.concat([test_a, test_b])
test_ab_all = pd.concat([test_ab_all, data[['channel', 'zip_code', 'offer']]], axis = 1 , join = 'inner')
test_ab_all['treatment'] = test_ab_all['offer'].map(lambda x: 0 if x == 'No Offer' else 1)
test_ab_all['uplift_bins'], updown = pd.qcut(test_ab_all['uplift_score'], q = 10, retbins = True, duplicates = 'drop', labels = np.arange(1, 11))
test_ab_all

# 5.计算每个十分位上，实验组、对照组的真实转化率 c_pct = target求和 / 十分位内各自记录数
test_ab_all_group = test_ab_all.groupby(by = ['uplift_bins', 'treatment']).agg({'history': 'count', 'target': 'sum', 'pre_b': 'mean', 'pre_a': 'mean', 'uplift_score': 'mean'})
test_ab_all_group['c_pct'] = test_ab_all_group['target']/test_ab_all_group['history']


test_ab_all_group.columns = ['user_num', 'c_user_num', 'pre_b_mean', 'pre_a_mean', 'uplift_score_mean', 'c_pct']
test_ab_all_group

# 6.从以上数据中分离实验组、对照组数据
b_group = test_ab_all_group.loc[(slice(None), [1]),:]
a_group = test_ab_all_group.loc[(slice(None), [0]),:]

# multiindex处理方法
a_group_ = a_group.xs(key = 0, level = 1)
b_group_ = b_group.xs(key = 1, level = 1)

# 7.将以上十分位内的对照组数据拼接到实验组中，以计算每十分位内的真实增益
b_group_ = pd.concat([b_group_, a_group_['c_pct']], axis = 1)
b_group_.columns = ['user_num', 'c_user_num', 'pre_b_mean', 'pre_a_mean', 'uplift_score_mean', 'b_c_pct', 'a_c_pct']

# real_diff_pct 为 真实增益，拉齐后的实验组转化率 - 对照组转化率
b_group_['real_diff_pct'] = b_group_['b_c_pct'] - b_group_['a_c_pct'] 
b_group_.index = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
b_group_

plt.bar(b_group_.index, b_group_['real_diff_pct'])

3.4 gini曲线及AUUC

# 1. 分别划分十分位
test_a['uplift_bins'], updown = pd.qcut(test_a['uplift_score'], q = 10, retbins = True, duplicates = 'drop', labels = np.arange(1, 11))

test_b['uplift_bins'], updown = pd.qcut(test_b['uplift_score'], q = 10, retbins = True, duplicates = 'drop', labels = np.arange(1, 11))


# 2. 以uplift十分位进行聚合，计算每个十分位中的用户数、真实转化数、转化率
test_a_group = test_a.groupby(by = ['uplift_bins']).agg({'history': 'count', 'target': 'sum'})
test_a_group.columns = ['user_num', 'c_user_num']

test_a_group['kw_pct'] = test_a_group['c_user_num']/test_a_group['user_num']
test_a_group

test_b_group = test_b.groupby(by = ['uplift_bins']).agg({'history': 'count', 'target': 'sum'})
test_b_group.columns = ['user_num', 'c_user_num']

test_b_group['kw_pct'] = test_b_group['c_user_num']/test_a_group['user_num']
test_b_group


# 3. 合并实验组、对照组数据，并重命名列名
test_union_group = pd.concat([test_b_group, test_a_group], axis = 1)
test_union_group.columns = ['user_num_b', 'c_user_num_b', 'c_pct_b', 'user_num_a', 'c_user_num_a', 'c_pct_a']
test_union_group['uplift_score'] = test_union_group['c_pct_b'] - test_union_group['c_pct_a']
test_union_group

test_union_group.index = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
test_union_group


# 5. 添加实验组、对照组 总的用户数
test_union_group['total_b'] = test_union_group['user_num_b'].sum()
test_union_group['total_a'] = test_union_group['user_num_a'].sum()

# 6. 分别计算实验组、对照组 累计转化用户数
test_union_group['c_user_num_b_cums'] = test_union_group['c_user_num_b'].cumsum(axis = 0)
test_union_group['c_user_num_a_cums'] = test_union_group['c_user_num_a'].cumsum(axis = 0)

# 7. 计算累计的转化率之差
test_union_group['q_b_i'] = test_union_group['c_user_num_b_cums']/test_union_group['total_b']

test_union_group['q_a_i'] = test_union_group['c_user_num_a_cums']/test_union_group['total_a']

test_union_group['q_i'] = test_union_group['q_b_i'] - test_union_group['q_a_i']


# 8. 引入包画gini曲线，并计算AUUC
from numpy import trapz  # 利用梯度规则求解积分
from scipy.integrate import simps  # 利用辛普森积分法（Simpson's rule），以二次曲线逼近的方式取代矩形或梯形积分公式，以求得定积分的数值近似解。

x = np.r_[0, list(test_union_group.index)]
y = np.r_[0, list(test_union_group['q_i'])]

random_curve_area = simps([0, y[len(y) - 1]], [0,10], dx=0.001)  # 随机曲线与x轴围成的面积
gini_curve_area = simps(y, x, dx=0.001)   # gini曲线与x轴围成的面积
auuc = gini_curve_area - random_curve_area

fig, ax = plt.subplots()
ax.plot(x, y, c = 'green', label = 'gini curve')
ax.plot([0,10], [0, y[len(y) - 1]], c = 'blue', ls = '--', label = 'random curve')
ax.text(x = 7.5, y = 0.02, s = 'auuc: %f'%auuc )