前言

 红黑树的删除，较AVL树的删除比较抽象，同时也跟红黑树的插入的区别较大，但大体上的思路还是基于普通二叉搜索树的基础上进行讨论的。

浅浅的铺垫一下:

1. 需要清楚普通二叉树的删除，可见AVL树的删除文章开头。
2. 四种旋转的操作（只需操作）得熟记于心，可见AVL树的插入与验证
3. 红黑树的插入的变色原理得清楚，可见红黑树的插入与验证

正文

1.所删除的结点为红色

• 红色的删除最为简单，因为红色结点所连接的结点都是黑色！

为了便于描述，我们这里将所删除的结点称之为delnode

1.1delnode的左右都为空

不管delnode在左边还是在右边，我们只需要改变父节点的delnode指向为空即可。

1.2delnode的左为空，且右不为空

• 如果delnode右不为空，则其右为黑色，但是每条路径的黑色结点数必然相同，则delnode的左结点必然也为黑色，与条件的左为空相悖，因此情况不存在。

1.3delnode的左不为空，右为空

• 如果delnode左不为空，则其左为黑色，但是每条路径的黑色结点数必然相同，则delnode的右结点必然也为黑色，与条件的右为空相悖，因此情况不存在。

1.4delnode的左不为空，且右不为空

• 根据普通二叉搜索树，这里要找左子树的最大结点，进行值交换，然后再删除找到的左子树的最大节点，其如果为红色，则转换为1.1情况。

• 因此：delnode为红色只有一种处理方法。

2.所删除的结点为黑色

• 重头戏来了！
  为了便于描述，我们这里将所删除的结点称之为delnode

 先对delnode进行分析，既然为黑色，其左节点或者右节点为红色，或者左右结点都为红色，或者左右都为空，当然分析到这里还不够，我们还要对其uncle进行分析。

2.1 调整后所在树每条路径黑色结点的个数不发生变化

2.1 左结点不为空，右节点为空

• 左节点只能是红色，因为每条路径的黑色结点数是一样的。
  

不管delnode为parent的左结点还是右节点，parent的指向delnode的节点改为指向delnode的左边，再将delnode的左边结点颜色改为黑色即可。

2.2 左结点为空，右节点不为空

不管delnode为parent的左结点还是右节点，parent的指向delnode的节点改为指向delnode的右节点，再将delnode的右边结点颜色改为黑色即可。

2.3 左右结点都为空

设parent为delnode的父节点，父节点另一个链接的结点设为uncle。
 如果下面分析delnode结点为左右有些太冗余了，我们只分析cur(delnode)为parent的左结点这一种情况，最后cur为parent右结点这一种情况，最后以图解的方式呈现。

2.3.1 uncle为黑色

2.3.1.1uncle的左节点为红色(右不为红)

1. 父节点为红色

• uncle右节点为黑色

此情况为delnode向上迭代的一种情况：

• uncle右节点为空

此时：cur为delnode/向上迭代的一种情况。

2. 父节点为黑色

• uncle右节点为黑色

此情况为delnode向上迭代的一种情况。

• uncle右节点为空
  此情况为：cur为delnode
  

 总结分析方式是一样的，只是最后实际的变色是不一样的，我们可以从中发现一个变色规律：

1. 右左双旋
2. uncle_left赋值为黑色

2.3.1.2uncle的右节点为红色

1. 父节点为黑色

• uncle的左节点为黑色
  

• uncle的左节点为红色

2. 父节点为红色

• uncle的左节点为黑色

• uncle的左节点为红色

 总结分析方式是一样的，只是最后实际的变色是不一样的，我们可以从中发现一个变色规律：

1. 左旋
2. parent的颜色赋值给uncle
3. parent的颜色与uncle_right的颜色赋值为黑色

2.3.1.3uncle的左右结点都为黑色

• parent为红色

2.3.2 uncle红色

• uncle为红色，其连接的结点必然为黑色，又因为delnode为黑，所以uncle的左右结点必然存在。

2.3.2.1 uncle的左右结点都为黑

整棵树每条路径的黑色结点数不变，但是此时cur的uncle更新为un_left为黑色，继续对uncle的情况进行判断即可，更新后parent为红且uncle为黑，一定是高度不变化的一种情况之一，再判断一次即可。

2.2 调整后所在树每条路径黑色结点的个数发生变化

设parent为delnode的父节点，父节点另一个链接的结点设为uncle。

2.2.1 uncle为黑色

• 上面uncle为黑色且高度不变化的情况已经考虑过了，这里只剩下一种情况。

2.2.1.1 uncle的左右结点为黑色

• parent为黑色
  

整棵树每条路径的黑色结点数少一个，继续向上调整，cur等于parent，parent更新为cur的parent，最坏情况到根节点结束。

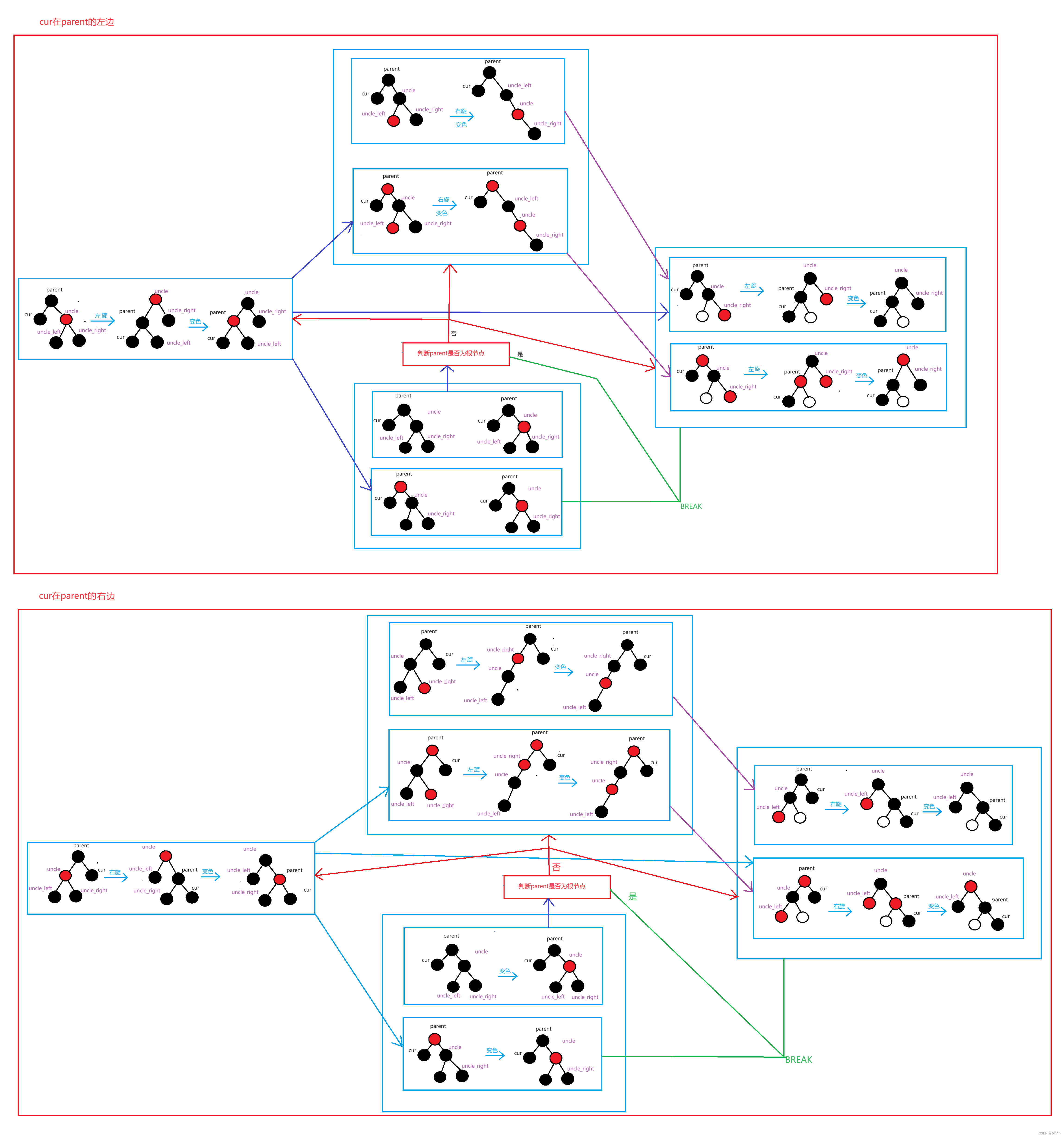
图解

实现代码

void ChangeColor(Node* cur,Node* parent)
{
	while (parent)
	{
		if (parent->_left == cur)
		{
			Node* uncle = parent->_right;
			//既然cur为黑结点，那么uncle就必然不可能为空。
			if (uncle->_col == RED)
			{
				//父节点必然为黑结点，uncle的左右孩子必然为黑色结点。

				//进行左旋
				RotateL(parent);
				uncle->_col = BLACK;
				parent->_col = RED;

				//无需更新。
			}
			else
			{
				//再次强调uncle是不可能为空的，因为cur为黑色结点。

				//需要对uncle的左右孩子进行判断
				Node* un_right = uncle->_right;
				Node* un_left = uncle->_left;
				//un_right 与 un_left可能为空。
				// 
				//uncle的左结点为红色,右节点为黑色或者为空
				if (un_left && un_left->_col == RED 
				&& (un_right == nullptr || un_right->_col == BLACK))
				{
					//先变色
					uncle->_col = RED;
					un_left->_col = BLACK;
					//进行右旋
					RotateR(uncle);

				}
				//uncle的右节点为红色,uncle的左节点为黑色或者红色或者为空
				else if (un_right && un_right->_col == RED)
				{
					//先变色
					uncle->_col = parent->_col;
					parent->_col = un_right->_col = BLACK;
					//进行左旋
					RotateL(parent);

					//到此处达到平衡
					break;
				}
				//uncle的左节点为黑色且右节点也为黑色。
				else
				{
					//直接进行变色
					uncle->_col = RED;
					if (parent->_col == BLACK)
					{
						//更新cur结点与parent结点，继续向上更新。
						cur = parent;
						parent = cur->_parent;
					}
					else//父节点为红色
					{
						//变父节点为黑色，跳出循环。
						parent->_col = BLACK;
						break;
					}
				}
			}

		}
		else
		{
			Node* uncle = parent->_left;

			//uncle结点为红色
			if (uncle->_col == RED)
			{
				//变色保证路径的黑色结点的个数不变。
				//此时新更新的uncle的颜色变为黑色。
				uncle->_col = BLACK;
				parent->_col = RED;
				//父节点，un_left与un_right皆为黑色。
				RotateR(parent);
			}
			else
			{
				//uncle结点为黑色
				Node* un_right = uncle->_right;
				Node* un_left = uncle->_left;
				//uncle的右节点为红色，且左节点为黑色或者空
				if (un_right && un_right->_col == RED &&\
				 (un_left == nullptr || un_left->_col == BLACK))
				{

					//变色保证路径的黑色结点数不发生变化
					uncle->_col = RED;
					un_right->_col = BLACK;
					//以uncle结点进行进行左旋，此时un_right成uncle
					RotateL(uncle);

				}
				//uncle的左节点为红色，且右节点为黑/红/空。
				else if (un_left && un_left->_col == RED)
				{
					//先变色保证路径的黑色结点数不发生变化
					uncle->_col = parent->_col;
					parent->_col = un_left->_col = BLACK;
					//进行右旋
					RotateR(parent);
					break;
				}
				//uncle的左右结点都为黑色
				else
				{
					uncle->_col = RED;
					if (parent->_col == BLACK)
					{
						cur = parent;
						parent = cur->_parent;
					}
					else
					{
						parent->_col = BLACK;
						break;
					}
				}
			}

		}
	}
}

总结

• 理解的难点

1. 分类讨论，逐步分析，拆解与转换问题。
2. 旋转与变色的底层逻辑是增加待删除路径的黑色结点数，同时保证另一棵树的每一条路径的黑色结点数不发生变化，结果是树的每条黑色结点的路径数不变。
3. 时间与耐心。

 博主认为这三点缺一不可。

 红黑树的删除比插入是难了不少的，不像AVL树的删除，可以复用之前的轮子，这里还得重新分析，每一种情况，博主看网上的大多数的讲解是比较抽象的，所以这里特意举了很多实际的例子进行分析，希望能降低一些红黑树插入的难度。

 最后如果本篇文章对您有所帮助的话，不妨点个赞鼓励一下吧！