“傻瓜”学计量——时空分异分析(全局/局域莫兰指数 Moran’s I)及stata代码(为爱发电)
“傻瓜”学计量——时空分异分析(全局/局域莫兰指数 Moran’s I)及stata代码(为爱发电)免费
提纲:
时空统计分析方法的原理、及知识框架
全局/局域 Moran’s I 的stata指令
1 时空统计分析方法的原理
首先需要了解空间异质性(spatial heterogeneity)这个概念。
1.1 空间异质性(spatial heterogeneity)
这个名词来源于生态学,说的是各种物体在空间上的分布是有多样性的,有些地方植物的种类就相当的复杂,有的地方相对来说就没有那么多种类。
举个简单的例子:
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼《题西林壁》
“异”,大家都知道,就是不同的、有差别的意思。 “质”,就是事物的根本、特性,本体,本性的意思。但是在地理学,特别是空间统计学上面,空间异质性,一般指的是因为观察位置的不同,而产生的不同观测结果。
正如前面苏轼的那首诗里面写的,庐山本体就在那个地方,它本身是不会发生任何变化的,但是因为你所处的位置不同,获得的观察结果也不同。这种因为观察位置不同,而引发的不同特征,就是所谓的空间异质性。
这种差异,有的时候是因为观察位置的不同,而引发的测量错误,就如同上面那首诗,不同位置看见不同的庐山,但是有的确是因为观察得距离和空间变化,所以引发的有意义的差异性。
| 这里补充一点知识: 是指无论在政治经济领域,还是在生物地理方面,空间关联性现象是普遍存在的,且近处比远处关联性更强。托布勒将此称为地理学第一定律。 |
1.2 空间依赖关系
在时空统计分析中,时常需要借用空间权重矩阵来反映空间依赖关系,所以可以说空间权重矩阵的设置在一定程度上算是多数时空统计分析的前提与基础。主要分为以下两大类:
1.2.1 “邻接性”空间依赖关系
| Bishop邻接 | A与所有的B都是共顶点连接 |  |
| Rock邻接 (也叫“车式邻接”) | A与所有的B都是公共边连接 |  |
| Queen邻接 (也叫“后式邻接”) | A与所有的B既是共顶点连接又是公共边连接 |  |
当两个区域存在“邻接”关系时记为“1”,“不邻接”时则记为“0”。(后文莫兰指数中W矩阵有用到)
可以发现,Queen邻接既包括公共边也包括公共顶点,因此实际上应该是Bishop邻接和Rock邻接的结合。
此外,值得注意的是,在实际研究过程中,由于地图形状多为不规则形,所以Bishop邻接,即公共顶点的空间相邻关系在现实情况中极其罕见。所以在大多数的时空统计分析中,选择以Queen连接设置的空间权重矩阵较为常见。
( 注意:所谓“车式”或“后式”完全是由于其邻接方向与国际象棋“车“或“ 后”的行走规定方向一致,而被形象比喻称之的。根据“车式”或“后式”邻接规则创建的空间权重矩阵具有对称性。)
1.2.2 “距离性”空间依赖关系
距离矩阵在空间计量经济学中,可分为狭义距离和广义距离。
| 狭义距离 | 几何距离,最为常用的即为地理距离加权矩阵 | 权重计算方法:两个地理区域中心位置之间的距离(一般指两地之间的质心距离)差值的倒数。 |
| 广义距离 | 非几何距离,较为常用的是经济距离权重矩阵 | 权重计算方法:两个地理区域的人均地区生产总值之间的差值的倒数。 |
1.3 空间关联性:包括自关联性和交叉关联性
| 空间关联性的分类 | ||
| 分类 | 概念 | 举例子 |
| 空间自关联性 | 是指同一变量在不同地域单元(如县、地区、省和国家,或植物区、动物区和土攘区等)之间的相关性。 | 比如,各个地域单元的GDP与其周围地域单元的GDP之间有在着正相关性。 |
| 空间交叉关联性 | 是指两个不同变量在不同地域单元之间的相关性。 | 比如,各个地域单元的交通运输业产值与其周围地域单元的公路密度之间存在着正相关性。 |
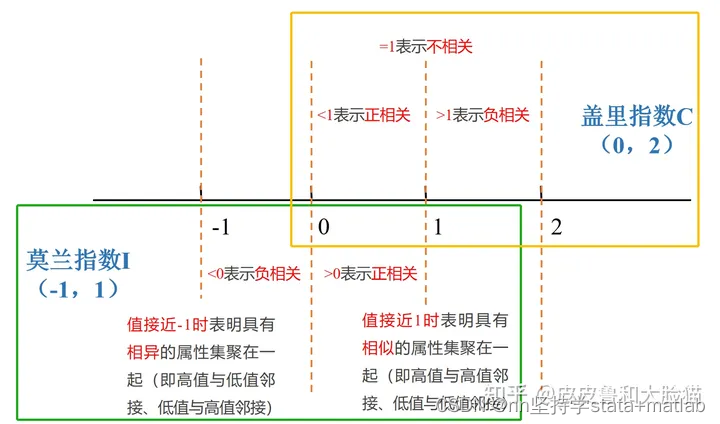
2 数据指标:莫兰指数+盖里指数
探索性空间数据分析,主要用于探测一些变量的空间关联性和集聚现象。
某一变量在空间上发生集聚,意味着在一定区域内,这一变量在各个地域单元之间具有自相关性。因此,空间自相关性可以看作是一种反映集聚现象的尺度。
探索性空间数据分析主要使用的两类工具:
| 种类 | 用途 | 常用指标 | |
| 第一类 | 用来分析整个区域关联性的指数,该类指数称为全局空间关联性指标。
| 全局莫兰Moran指数I | 在实际研究空间关联性中,很少使用双变量全局莫兰指数Ixy。 莫兰指数I是空间自相关回归方程系数的估计值,其取值范围只能在-1到1之间。
|
| 盖里Geary指数C | 与莫兰指数I相似,盖里指数C也是一个检验空间关联性和集聚问题的指数。计算莫兰指数I时,用的是中值离差的叉乘;但是,盖里指数C强调的是观察值之间的离差。 盖里指数C的取值范围一般在0到2之间(在极端情况下,它也会大于2)。
| ||
| 第二类 | 用来分析区域内各个地域单元关联性的指数,该类指数称之局部空间自相关性指标 | 局部莫兰指数I | 安塞林(Anselin)1995年提出一个局部莫兰指数(简称LISA)用来检验局部地区是否存在变量集聚现象。地域单元i的局部莫兰指数用来度量它和其周围地域单元之间的关联性。
|
| 盖里指数C | 基斯(Getis)和奥德(Ord)在1992年提出一个局部盖里指数G;用来检验局部地区是否存在变量集聚现象。这个指数用来检验:局部地区是否有高值或低值在空间上趋于集聚。
| ||
一般来说全局空间关联性指标可以分为:
| 自关联性 | 是反映同一变量在研究区域内的自相关性 |
| 交叉关联性 | 是反映两个不同变量在研究区域内的相关性。 |
3 全局/局域 莫兰指数 stata指令
空间自相关性(Spatial Autocorrelation)分析:通常用于研究空间某点的观察值是否与其相邻点的观察值存在相关性,可揭示研究变量在研究区域中的空间分布特性,本文主要将全局莫兰指数(Moran's I)和局部莫兰指数(Local Moran's I)作为空间自相关分析的指标。
全局莫兰指数:主要从总体上反映研究对象是否具有空间自相关性,但其并不能反映这种空间自相关的方向以及程度;
局部莫兰指数:主要反映研究对象在研究区域中究竟呈现出何种空间聚集形态。
w矩阵:权重矩阵。横纵坐标分别代表31个省份。简单形式:二元。首先对角线都改成0。根据临近程度选择1/0。
w矩阵命名为:W.dta
开始运行:
| 1 | 安装命令族 | ssc install spwmatrix findit spatwmat 在弹出的对话框中选择sg162 from http://www.stata.com/stb/stb60 点击click here to install | |
| 2 | 整理数据 | spwmatrix import using E:Stata\matrix.gal,wname(W) rowstand xport(m,dat) 使用Excel打开刚保存的dat文件,增加第1行为表头,第1列不需要增加(此为固定格式,不按此格式会报错) 将全部数据复制粘贴到Stata数据表中,保存为dta文件 | 第一:权重矩阵 *.gal:Geoda导出的空间权重矩阵 wname后括号中W是Stata中矩阵名称 rowstand行标准化 xport输出 括号内m是文件名 需要注意的是ID需要以1起始,如果以0起始则会报错 |
| 第二:要研究的数据 注意,要和权重矩阵中的数据排序顺序一致 | |||
| 3 | 引用权重矩阵 | spatwmat using weight.dta | 用于全局莫兰 weight.dta:权重矩阵文件的名字 |
| spatwmat using weight.dta standardize | 用于局部莫兰 weight.dta:权重矩阵文件的名字 standardize 局部莫兰数据格式 | ||
| 4 | 定义面板数据 | xtset id year | |
| 5 | 全局性莫兰I指数指令 | spatgsa a1,weights(w) moran | a1:是一年的变量。包含所有省份的数据。 |
| 局部莫兰I指数指令 | splagvar a1,weights(w) moran graph(moran) symbol(n) | ||
| 6 | 对每一年/变量进行莫兰指数的测算 | preserve keep if year ==2001 spatlsa x1,weights(w) moran geary twotail | 全局莫兰散点图 蓝色部分:针对要做的变量进行改变。一般是Y值和核心变量x1; 橙色部分:莫兰指数的测算要一年一年来。测算哪一年就填哪一年 |
| preserve keep if year ==2001 splagvar x1,wname(w) wfrom(Stata) moran(x1) plot(x1) restore | 局部莫兰散点图 蓝色部分:针对要做的变量进行改变。一般是Y值和核心变量; 橙色部分:莫兰指数的测算要一年一年来。测算哪一年就填哪一年 | ||
| 6.5 | 循环 全局莫兰测算 | forvalue i = 2004/2016{ preserve keep if year==`i' spatgsa y,weights(W) moran twotail restore } | 简化工作量。 详细见倒数第二条链接 |
4 结果解读
第一:看i的指数
第二:看p值是否显著

开放原子开发者工作坊旨在鼓励更多人参与开源活动,与志同道合的开发者们相互交流开发经验、分享开发心得、获取前沿技术趋势。工作坊有多种形式的开发者活动,如meetup、训练营等,主打技术交流,干货满满,真诚地邀请各位开发者共同参与!
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容






所有评论(0)