多元线性回归分析

回归分析是数据分析中最基础也是最重要的分析工具，绝大多数的数据分析问题，都可以使用回归的思想来解决。回归分析的任务就是，通过研究自变量X和因变量Y的相关关系，尝试去解释Y的形成机制，进而达到通过X去预测Y的目的。
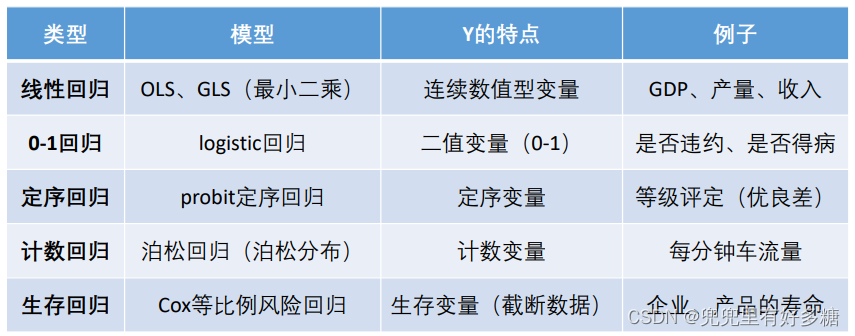
常见的回归分析有五类：线性回归、0‐1回归、定序回归、计数回归和生存回归，其划分的依据是因变量Y的类型。本讲我们主要学习线性回归。

一、回归分析：研究X和Y之间相关性的分析

三个关键词：

1. 相关性
2. Y
3. X

第一个关键词：相关性

统计数据表明：游泳死亡人数越高，雪糕卖得越多（游泳死亡人数和雪糕售出量之间呈显著正相关）
可以下结论：吃雪糕就会增加游泳死亡风险吗？
（因为吃雪糕，所以游泳死亡风险增加了）

相关性 ≠ 因果性
在绝大多数情况下，我们没有能力去探究严格的因果关系，所以只好退而求其次，改成通过回归分析，研究相关关系。
听起来比较悲观？其实不是的。为什么？因为，这个退而求其次的方案，比你瞎拍脑袋好多了去了。

第二个关键词：Y

Y是什么？俗称因变量。因为别人的改变，而改变的变量。
在实际应用中，Y常常是我们需要研究的那个核心变量。
（1）经济学家研究经济增长的决定因素，那么Y可以选取GDP增长率（连续数值型变量）。
（2）P2P公司要研究借款人是否能按时还款，那么Y可以设计成一个二值变量，Y=0时代表可以还款，Y=1时代表不能还款（0‐1型变量）。
类似的0-1型变量还有：

（3）消费者调查得到的数据（1表示非常不喜欢，2表示有点不喜欢，3表示一般般，4表示有点喜欢，5表示非常喜欢）（定序变量）。
（4）管理学中RFM模型：F代表一定时间内，客户到访的次数，次数其实就是一个非负的整数。（计数变量）
（5）研究产品寿命、企业寿命甚至是人的寿命（这种数据往往不能精确的观测，例如现在要研究吸烟对于寿命的影响，如果选取的样本中老王60岁，现在还活的非常好，我们不可能等到他去世了再做研究，那怎么办呢？直接记他的寿命为60+，那这种数据就是截断的数据）（生存变量）

第三个关键词是：X

X是用来解释Y的相关变量，所以X被称为自变量。
回归分析的任务就是，通过研究X和Y的相关关系，尝试去解释Y的形成机制，进而达到通过X去预测Y的目的。

回归分析的作用

1. 回归分析要去识别并判断：哪些X变量是同Y真的相关，哪些不是。统计学中有一个非常重要的领域，叫做“变量选择”—选择出真正与Y有关的变量，去掉不相关的因素。（逐步回归法—把X逐一检测对Y的影响，挑选出对Y有显著影响的那些自变量X）
2. 去除了那些同Y不相关的X变量，那么剩下的，就都是重要的、有用的X变量了。接下来回归分析要回答的问题是：这些有用的X变量同Y的相关关系是正的呢，还是负的？
3. 在确定了重要的X变量的前提下，我们还想赋予不同X不同的权重，也就是不同的回归系数，进而我们可以知道不同变量之间的相对重要性。（X的量纲各不相同时，需要去量纲，对数据进行标准化操作）

这就是回归分析要完成的三个使命：
第一、识别重要变量；
第二、判断相关性的方向；
第三、要估计权重（回归系数）

回归分析的分类：

（OLS：普通最小二乘，GLS：广义最小二乘）

数据分类：

对每一种数据我们用到的建模方法会有区别，所以有必要区分各种数据类型。

建模比赛中，前两种数据类型最常考到；面板数据较为复杂，是经管类学生在中级计量经济学中才会学到的模型。
横截面数据往往可以使用回归来进行建模，我们通过回归可以得到自变量与因变量之间的相关关系以及自变量的重要程度。
时间序列数据往往需要进行我们进行预测，时间序列模型的选择也很多，大家需要选择合适的模型对数据进行建模

横截面数据：在某一时点收集的不同对象的数据
例如：
（1）我们自己发放问卷得到的数据
（2）全国各省份2018年GDP的数据
（3）大一新生今年体测的得到的数据

时间序列数据：对同一对象在不同时间连续观察所取得的数据。
例如：
（1）从出生到现在，你的体重的数据（每年生日称一次)。
（2）中国历年来GDP的数据。
（3）在某地方每隔一小时测得的温度数据。

面板数据：横截面数据与时间序列数据综合起来的一种数据资源。
例如：
2008‐2018年，我国各省份GDP的数据。

【数据收集网站】

上面的数据多半都是宏观数据，微观数据市面上很少
大家可以在人大经济论坛搜索
https://bbs.pinggu.org/

二、线性回归

根据我们上边介绍的，做线性回归我们需要的数据是横截面数据。

我们先从一元线性回归开始说起：

一元线性回归

首先回顾一下什么是一元线性函数的拟合：

之后用一个损失函数来评价拟合的这条直线的好坏。损失函数我们用的是残差平方和。

那么什么又是一元线性回归模型呢：

最大的不同有两点：

1. 回归模型中必然要区分的是自变量和因变量，而拟合模型中并不关注这一点，整个坐标点（x,y）的值是作为一个整体存在的
2. 回归模型的函数多了一个截距，在这里成为扰动项。

对线性的理解

我们的线性模型基本式子如下：

μ为无法观测的且满足一定条件的扰动项。

那么思考我将上式略作变化后得到的如下几个式子还是不是线性呢：

答案是：仍满足线性。因为不论式子中出现Lnx或者是x的二次方，我们都可以用一个新的变量xi来替代，从而变为一次的，线性的。

也就是线性假定并不要求初始模型都呈上述的严格线性关系。自变量与因变量可通过变量替换而转化成线性模型。
所以如下显示的几种模型都是可以称作线性模型。
在建立模型的时候应该根据数据的具体特征选择用严格的线性模型还是用以下这种经过变形的模型。
那么如果我们观察到数据特征比较适合用下边的第一行的模型，我们如何将自变量进行对数化处理呢？
可以用Excel，Matlab，Sata等软件。
这一步其实叫做线性回归建模之前的数据预处理。
那么用这些软件对数据进行对数化之后就可以用对数化之后的自变量进行建模了。

以下来演示一下如何用Excel对数据进行预处理：
计算价格的自然对数：

计算销售量的自然对数：

计算价格的平方：

对数据预处理之后就可以导出到建模软件中了。

回归系数的解释：

可以看到，引入了新的自变量价格后，对回归系数的影响非常大！！！
原因：遗漏变量导致的内生性

内生性的探究

什么是内生性?

这个干扰项μi包含什么？
包含了所有与y相关，但未添加到回归模型中的变量。
当我们没有把应该考虑的所有自变量都考虑进去，然后添加到模型当中去的时候，这是就势必会导致μi中会体现出这些自变量的影响，这就叫做内生性。

简而言之：如果我们的模型考虑的自变量不全，会导致本来不是自变量的干扰项μi带有某些我们没有考虑进去的自变量的变化规律，这样导致的问题就是对我们已考虑的自变量的回归系数的评定影响会很大，不满足无偏性和一致性。
所以我们一定要尽可能把所有应该考虑的自变量考虑全。
比如上边那个例子：

同一组模型，我一开始只用了一个自变量表示，最后算出的回归系数是2.3，而后面用了两个自变量时，回归系数的变化非常大，这就说明我一开始遗漏了自变量，说明这个一开始的模型具有内生性的问题。

【内生性的蒙特卡罗模拟】

下面我们用matlab来演示一下内生性对回归系数估计的影响：

假设有一个二元变量的函数，但是我们用一元的线性模型来回归。那么在无偏估计的情况下，拟合出的k应该是2。
但是由于μ的内生性影响，结果却不一定，
所以我们评估μ与自变量的相关性（也就是在评估内生性的影响大小），会怎么影响k的取值。

对应的matlab代码如下：

%% 蒙特卡洛模拟：内生性会造成回归系数的巨大误差
times = 300;  % 蒙特卡洛的次数
%首先初始化两个300行1列（之所以是300行，是因为第一行代码规定了代码运行的次数，也就是这些数据的个数）的容器来存储后期运行出的数据：
R = zeros(times,1);  % 用来储存扰动项u和x1的相关系数
K = zeros(times,1);  % 用来储存遗漏了x2之后，只用y对x1回归得到的回归系数
for i = 1: times
    n = 30;  % 样本数据量为n，也就是点的个数为30个
    x1 = -10+rand(n,1)*20;   % x1在-10和10上均匀分布，大小为30*1，x1就是一个列向量，代表这些点位的横坐标。
    u1 = normrnd(0,5,n,1) - rand(n,1);  % 随机生成一组随机数
    x2 = 0.3*x1 + u1;   % x2与x1的相关性不确定， 因为我们设定了x2要加上u1这个随机数
    % 这里的系数0.3我随便给的，没特殊的意义，你也可以改成其他的测试。
    u = normrnd(0,1,n,1);  % 扰动项u服从标准正态分布
    y = 0.5 + 2 * x1 + 5 * x2 + u ;  % 构造y
    k = (n*sum(x1.*y)-sum(x1)*sum(y))/(n*sum(x1.*x1)-sum(x1)*sum(x1)); % y = k*x1+b 回归估计出来的k
    K(i) = k;
    u = 5 * x2 + u;  % 因为我们回归中忽略了5*x2，所以扰动项要加上5*x2
    r = corrcoef(x1,u);  % 2*2的相关系数矩阵
    R(i) = r(2,1);
end
plot(R,K,'*')
xlabel("x_1和u'的相关系数")
ylabel("k的估计值")

最后得到的图如下：

横坐标相关系数绝对值越大，代表内生性越大。
可以看出相关系数为0时，也就是内生性不存在时，k的估值正好是2。

核心解释变量和控制变量

无内生性（no endogeneity）要求所有解释变量均与扰动项不相关。
这个假定通常太强，因为解释变量一般很多（比如，5‐15个解释变量），且需要保证它们全部外生。是否可能弱化此条件？答案是肯定的，如果你的解释变量可以区分为核心解释变量与控制变量两类。

核心解释变量：我们最感兴趣的变量，因此我们特别希望得到对其系数的一致估计（当样本容量无限增大时，收敛于待估计参数的真值 ）。
控制变量：我们可能对于这些变量本身并无太大兴趣；而之所以把它们也放入回归方程，主要是为了 “控制住” 那些对被解释变量有影响的遗漏因素。
在实际应用中，我们只要保证核心解释变量与𝝁不相关即可。

所以在实际操作过程中，我们应该把所有的变量区分为“核心解释变量”和“控制变量”两类。只要保证核心解释变量与𝝁不相关即可。

那么如何做到这一点呢，我们下篇文章再说。