线性系统的稳态误差(静态误差)

概述

• 稳态误差是系统的稳态性能指标，是对系统控制精度的衡量
• 对稳定的系统研究稳态误差才有意义
• 通常把在阶跃输入作用下没有原理性稳态误差的系统称为无差系统，而把有原理性误差的系统称为有差系统

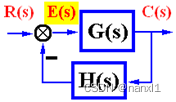
误差与稳态误差

按输入端定义的误差

$$E(s)=R(s)-C(s)H(s)$$

按输出端定义的误差

$$E^{\prime }(s)=\frac{R(s)}{H(s)}-C(s)$$

稳态误差

$$\{\begin{array}{l}静态误差:e_{ss}={\lim }_{t\to \infty }e(t)=e(\infty )\\ 动态误差:误差中的稳态分量e_s(t)\end{array}$$

Note

• $E(s)=H(s)\cdot E^{\prime }(s)$
• 一般来说按输入端定义的误差计算，因为该种情况下的物理量一般都能直接测量
• 分析系统误差时，一般计算静态误差

计算稳态误差的一般方法(重点)

• 判定系统的稳定性(必要条件、劳斯判据等)
• 求误差传递函数 ${\Phi }_e(s)=\frac{E(s)}{R(s)},{\Phi }_{en}=\frac{E(s)}{N(s)}$
• 用终值定理求稳态误差 $e_{ss}={\lim }_{s\to 0}s[{\Phi }_e(s)R(s)+{\Phi }_{en}(s)N(s)]$

例题

例1 系统结构图如图所示，已知$r(t)=n(t)=t$，求系统的稳态误差

$$\begin{array}{rl}{\Phi }_e(s)& =\frac{E(s)}{R(s)}=\frac{1}{1+\frac{K}{s(Ts+1)}}=\frac{s(Ts+1)}{s(Ts+1)+K}\\ D(s)& =T{s}^2+s+K=0,系统稳定\\ \Phi (en)& =\frac{E(s)}{N(s)}=-\frac{\frac{K_n}{T_{n}s+1}}{1+\frac{K}{s(Ts+1)}}=-\frac{K_{n}s(Ts+1)}{[s(Ts+1)+K](T_{n}s+1)}\\ e_{ss}& =\underset{s\to 0}{\lim }s[R(s){\Phi }_e(s)+N(s){\Phi }_{en}(s)]=\underset{s\to 0}{\lim }[\frac{Ts+1}{s(Ts+1)+K}-\frac{K_n(Ts+1)}{[s(Ts+1)+K](T_{n}s+1)}]\\ & =\frac{1}{K}+\frac{K_n}{K}=\frac{1+K_n}{K}\end{array}$$

例2 系统结构图如图所示，求$r(t)$分别为$A\cdot 1(t),At,A{t}^2/2$ 时系统的稳态误差

$$\begin{array}{rl}{\Phi }_e(s)& =\frac{E(s)}{R(s)}=\frac{1}{1+\frac{K}{s(Ts+1)}}=\frac{s(Ts+1)}{s(Ts+1)+K}\\ D(s)& =T{s}^2+s+K系统稳定\\ e_{ss}& =\underset{s\to 0}{\lim }s\cdot {\Phi }_e(s)R(s)\\ 当& r(t)=A\cdot 1(t)时，R(s)=\frac{A}{s}\\ e_{ss}& =\underset{s\to 0}{\lim }A\cdot \frac{s(Ts+1)}{s(Ts+1)+K}=0\\ 当& r(t)=At时，R(s)=\frac{A}{s^2}\\ e_{ss}& =\underset{s\to 0}{\lim }A\frac{Ts+1}{s(Ts+1)+K}=\frac{A}{K}\\ 当& r(t)=A{t}^2/2时，R(s)=\frac{A}{s^3}\\ e_{ss}& =\underset{s\to 0}{\lim }\frac{A}{s}\frac{Ts+1}{s(Ts+1)+K}=\underset{s\to 0}{\lim }\frac{A}{sK}=\infty \end{array}$$

• $e_{ss}$与系统自身的参数结构有关
• $e_{ss}$与外作用的类型有关(控制量，扰动量及作用点)
• $e_{ss}$与外作用的形式有关(阶跃，斜坡或加速度等)

静态误差系数法(掌握)

$$\begin{array}{rl}G(s)& =G_1(s)H(s)=\frac{K({\tau }_{1}s+1)...({\tau }_{m}s+1)}{s^v(T_{1}s+1)...(T_{n-v}s+1)}=\frac{K}{s^v}{G}_0(s)\\ G_0(s)& =\frac{({\tau }_{1}s+1)...({\tau }_{m}s+1)}{(T_{1}s+1)...(T_{n-v}s+1)}\underset{s\to 0}{\lim }{G}_0(s)=1\\ {\Phi }_e(s)& =\frac{E(s)}{R(s)}=\frac{1}{1+\frac{K}{s^v{G}_0(s)}}\\ e_{ss}& =\underset{s\to 0}{\lim }s{\Phi }_e(s)R(s)=\underset{s\to 0}{\lim }s\cdot R(s)\cdot \frac{1}{1+\frac{K}{s^v}{G}_0(s)}\end{array}$$

核心公式(***)

$$e_{ss}=\underset{s\to 0}{\lim }s{\Phi }_e(s)R(s)=\underset{s\to 0}{\lim }s\cdot R(s)\cdot \frac{1}{1+\frac{K}{s^v}{G}_0(s)}$$

• 稳态误差$e_{ss}$只与输入$r(t)$和系统结构参数$(K,v)$有关
• 该方法的本质是将$e_{ss}$的表达式转换成与 输入信号和系统结构参数相关的形式；因此一旦确定了输入信号和系统的结构参数，能迅速得到静态误差
• K: 系统的开环增益
• v: 表示系统类别

几个重要的系数

首先进一步将$e_{ss}$化简
$$e_{ss}=\underset{s\to 0}{\lim }s\cdot R(s)\cdot \frac{1}{1+\frac{K}{s^v}}$$

静态位置误差系数: $K_p={\lim }_{s\to 0}\frac{K}{s^v}$

$$\begin{array}{rl}当r(t)& =A\cdot 1(t)时,R(s)=\frac{A}{s}\\ e_{ss}& =\frac{A}{1+{\lim }_{s\to 0}\frac{K}{s^v}}\\ K_p& =\underset{s\to 0}{\lim }\frac{K}{s^v}称为静态位置误差系数\\ e_{ssp}& =\frac{A}{1+K_p}\end{array}$$

静态速度误差系数: $K_v={\lim }_{s\to 0}\frac{K}{s^{v-1}}$

$$\begin{array}{rl}当r(t)& =A\cdot t时,R(s)=\frac{A}{s^2}\\ e_{ss}& =\underset{s\to 0}{\lim }\frac{A}{s}\cdot \frac{1}{1+\frac{K}{s^v}}=\frac{A}{{\lim }_{s\to 0}\frac{K}{s^{v-1}}}\\ K_v& =\underset{s\to 0}{\lim }\frac{K}{s^{v-1}}称为静态速度误差系数\\ e_{ssv}& =\frac{A}{K_v}\end{array}$$

静态加速度误差系数: $K_a={\lim }_{s\to 0}\frac{K}{s^{v-2}}$

$$\begin{array}{rl}当r(t)& =\frac{A}{2}{t}^2时,R(s)=\frac{A}{s^3}\\ e_{ss}& =\underset{s\to 0}{\lim }\frac{A}{s^2}\cdot \frac{1}{1+\frac{K}{s^v}}=\frac{A}{{\lim }_{s\to 0}\frac{K}{s^{v-2}}}\\ K_a& =\underset{s\to 0}{\lim }\frac{K}{s^{v-2}}\\ e_{ssa}& =\frac{A}{K_a}\end{array}$$

重要结论

• V越大系统越容易稳定

• 输入信号中t的次数越大，系统越难稳定

• 当t的次数大于v时，稳态误差为$\infty$ 系统不稳定

• 当t的次数与v相等时，稳态误差存在，且只与开环增益K有关(其他参数已确定), 且只有V=0时计算公式不同

• 当t的次数小于v时，稳态误差为0 系统稳定

例题

例3

• $K、v$由开环传递函数$G(s)$确定
• $K$由$G(s)$的尾1形式求出
• $v$则看$G(s)$积分环节的个数

例4

例5

• 在主反馈口到干扰作用点之间的前向通道中提高增益、设置积分环节，可以同时减小或消除控制输入和干扰作用下产生的稳态误差。
• 静态误差系数法只有在输入输出的情况下可以使用

总结

计算稳态误差的一般方法(重点)

• 判定系统的稳定性(必要条件、劳斯判据等)
• 求误差传递函数 ${\Phi }_e(s)=\frac{E(s)}{R(s)},{\Phi }_{en}=\frac{E(s)}{N(s)}$
• 用终值定理求稳态误差 $e_{ss}={\lim }_{s\to 0}s[{\Phi }_e(s)R(s)+{\Phi }_{en}(s)N(s)]$

参考资料

【（新版！最清晰！去噪不炸耳！）自动控制原理 西北工业大学 卢京潮】